江苏省南京市溧水区2020-2021学年八年级下学期数学期末考试试卷

试卷更新日期：2021-08-17 类型：期末考试

进入出卷网下载

一、单选题

1. 如图所示的四张扑克牌中，在旋转180°后还是和原来一样的是（）

A、 B、 C、 D、

查看试题解析
2. 代数式 $\frac{\sqrt{a + 2}}{a + 1}$ 有意义的条件是（）

A、 $a > - 2$ 且 $a \neq - 1$ B、 $a \geq - 2$ C、 $a \leq - 2$ 且 $a \neq - 1$ D、 $a \geq - 2$ 且 $a \neq - 1$

查看试题解析
3. 下列调查问题中，适合采用普查的事件是 $($ $)$

A、调查全国中学生心理健康状况 B、调查某品牌电视机的使用寿命 C、调查中央电视台 $《$ 焦点访谈 $》$ 的收视率 D、调查你所在班级同学的身高情况

查看试题解析
4. 关于x的不等式x－a≥1.若x＝1是不等式的解，x＝－1不是不等式的解，则a的范围为（）

A、－2≤a≤0 B、－2＜a＜0 C、－2≤a＜0 D、－2＜a≤0

查看试题解析
5. 在▱ABCD中，对角线AC、BD相交于点O，若∠ABC＝90°，则下列结论错误的是（）

A、AC＝BD B、OA＝OB C、AC⊥BD D、AB＝CD

查看试题解析
6. 某商品经过两次降价，每瓶零售价由388元降为268元．已知两次降价的百分率相同，每次降价的百分率为x，根据题意列方程得（　　）

A、388（1+x）²=268 B、388（1﹣x）²=268 C、268（1﹣2x）=388 D、268（1+x）²=388

查看试题解析

二、填空题

7. 若 $\sqrt{x^{2} - 4 x + 4}$ =2-x，则实数x满足的条件是

查看试题解析
8. 若式子 $\sqrt{x - 2}$ 在实数范围内有意义，则x的取值范围是．

查看试题解析
9. 计算： $\frac{x}{x - 1}$ + $\frac{1}{1 - x}$ = ．

查看试题解析
10. 计算： $\sqrt{18} \div \sqrt{2} =$ ．

查看试题解析
11. 已知点A（x₁ ， y₁），B（x₂ ， y₂）是反比例函数y＝ $\frac{6}{x}$ 的图象上的两点，若x₁＞x₂＞0，则y₁y₂（填“＜”、“＞”或“＝”）

查看试题解析
12. 已知m、n是关于x的方程 $x^{2} - 3 x - 1 = 0$ 的两根，则代数式 $m^{2} - 2 m + n$ 的值为.

查看试题解析
13. 如图，在▱ABCD中，AC＝BC，∠CAD＝20°，则∠D的度数为°.

查看试题解析
14. “复兴号”是我国具有完全自主知识产权、达到世界先进水平的动车组列车.“复兴号”的速度比原来列车的速度每小时快40千米，提速后从北京到上海运行时间缩短了30分钟，已知从北京到上海全程约1320千米，求“复兴号”的速度.设“复兴号”的速度为x千米/时，依题意，可列方程为.

查看试题解析
15. 如图，已知四边形ABCD是平行四边形，BC=3AB，A，B两点的坐标分别是（﹣1，0），（0，2），C，D两点在反比例函数y= $\frac{k}{x}$ （x＜0）的图象上，则k的值等于．

查看试题解析
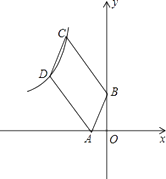16. 如图，在矩形ABCD中， AB＝3，AD＝10，点E在AD上且DE＝2.点G为AE的中点，点P为BC边上的一个动点，F为EP的中点，则GF＋EF的最小值为.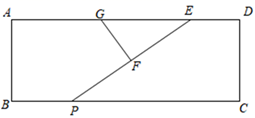

查看试题解析

三、解答题

17. 计算: $\sqrt{8} - \sqrt{\frac{1}{2}} + | - \frac{\sqrt{2}}{2} | - \sqrt{{(- 2)}^{2}}$

查看试题解析
18. 先化简，再求值： $\frac{x}{x + 1} - \frac{1}{x^{2} - 1} \div \frac{x - 1}{x^{2} - 2 x + 1}$ ，其中x＝ $\sqrt{3}$ +1.

查看试题解析
19. 解方程：

(1)、 $x^{2} + 6 x + 1 = 0$ ；

(2)、 ${(x - 3)}^{2} = 2 (x - 3)$ .

查看试题解析
20. 解方程 $\frac{3}{x^{2} - 9} + 1 = \frac{x}{x - 3}$ .

查看试题解析
21. 某校在初二年级开设了素描、舞蹈、合唱、魔方四个社团，为了解学生最喜欢哪一个社团，随机抽取了部分学生进行调查，并将调查结果绘制成了如下两幅不完整的统计图，请根据统计图回答下列问题：

(1)、本次抽样调查的样本容量是；

(2)、请将条形统计图补充完整；

(3)、已知该校初二年级共有学生900人，根据调查结果估计该校喜欢合唱和舞蹈社团的学生共有人.

查看试题解析
22. 已知抛物线 $y = x^{2} + 2 (m + 1) x + m^{2} - 1$ 与x轴交于 $A (x_{1}, 0)$ 、 $B (x_{2}, 0)$ 两点．

(1)、求m的取值范围；

(2)、 $若 x_{1}$ 、 $x_{2}$ 满足 ${(x_{1} - x_{2})}^{2} = 16 - x_{1} x_{2}$ ，求m的值．

查看试题解析
23. 如图，已知四边形ABCD是正方形，点B，C分别在直线 $y = 2 x$ 和 $y = k x$ 上，点A，D是x轴上两点.

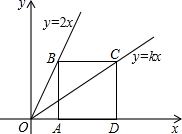(1)、若此正方形边长为2，k=.

(2)、若此正方形边长为a，k的值是否会发生变化？若不会发生变化，请说明理由；若会发生变化，求出a的值.

查看试题解析
24. 如图，已知 $△ A B C$ 中， $∠ B A C = 90 °$ ， $A B = A C = 6 \sqrt{2}$ ，点D为边 $B C$ 上一动点，四边形 $A D E G$ 是正方形，连接 $G C$ ，正方形对角线 $A E$ 交 $B C$ 于点F.

(1)、求证： $△ A B D ≌ △ A C G$ ；

(2)、若 $B D = 4$ ，求 $A E$ 的值；

(3)、若 $D F = 5$ ，求 $B D$ 的值.

查看试题解析
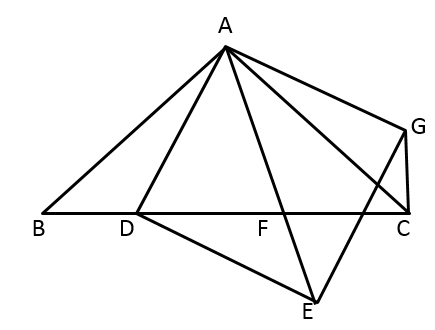25. 学校为了美化校园环境，在一块长40米，宽20米的长方形空地上计划新建一块长9米，宽7米的长方形花圃.

(1)、若请你在这块空地上设计一个长方形花圃，使它的面积比学校计划新建的长方形花圃的面积多1平方米，请你给出你认为合适的三种不同的方案；

(2)、在学校计划新建的长方形花圃周长不变的情况下，长方形花圃的面积能否增加2平方米？如果能，请求出长方形花圃的长和宽；如果不能，请说明理由.

查看试题解析
26. 同学们：八年级下册第9章我们学习了一种新的图形变换旋转，图形旋转过程中蕴含着众多数学规律，以图形旋转为依托构建的解题方法是解决各类几何问题的常用方法.

(1)、（问题提出）
如图①，在正方形ABCD中，∠MAN=45°，点M、N分别在边BC、CD上.求证：MN＝BM＋DN.

证明思路如下：

第一步：如图②，将 $△ A D N$ 绕点A按顺时针方向旋转90°得到△ABE，再证明E、B、M三点在一条直线上.

第二步：证明 $△ A E M ≌ △ A N M$ .

请你按照证明思路写出完整的证明过程.

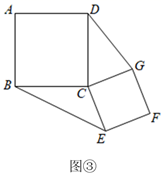
(2)、（初步思考）
如图③，四边形ABCD和CEFG为正方形，连接DG、BE，得到 $△ D C G$ 和 $△ B C E$ .

下列关于这两个三角形的结论：①周长相等； ②面积相等； ③∠CBE=∠CDG.

其中所有正确结论的序号是.

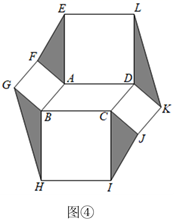
(3)、（深入研究）
如图④，分别以▱ABCD的四条边为边向外作正方形，连接EF，GH，IJ，KL.若▱ABCD的面积为8，则图中阴影部分（四个三角形）的面积之和为.

查看试题解析