广西壮族自治区贵港市2020-2021学年八年级下学期数学期末考试试卷
试卷更新日期：2021-08-17 类型：期末考试
一、单选题
-
1. 小凡的手机话费原有余额60元，与姐姐通话，话费余额随时间变化而变化.在这个过程中，因变量是（ ）A、话费余额 B、时间 C、60 D、小凡2. 如图，将 ABCD的一边BC延长至点E，若∠1=80°，则∠A等于（ ）
A、80° B、120° C、100° D、110°3. 将直线y＝4x＋3向下平移5个单位后，所得直线的表达式是（ ）A、y＝4（x＋5）x＋3 B、y＝4（x﹣5）x＋3 C、y＝4x＋8 D、y＝4x﹣24. 如图，Rt△ABC中，∠ACB=90°，CD⊥AB于点D，则下列结论不一定成立的是（ ）
A、∠1+∠2=90° B、∠3=60° C、∠2=∠3 D、∠1=∠45. 下列各曲线中能表示y不是x的函数的是（ ）A、
B、
C、
D、
6. 直角三角形两直角边长为6和8，则此三角形斜边上的中线的长是（ ）A、10 B、5 C、4 D、37. 已知点 在第四象限，且点 到 轴的距离是3，到 轴的距离是5，则点 的坐标是（ ）A、 B、 C、 D、8. 已知△ABC的三边分别为a，b，c，下列条件中，能判定△ABC为直角三角形的是（ ）A、2a=b＋c B、a：b：c=1： ：2 C、∠A：∠B：∠C=3：4：5 D、2∠A=∠B＋∠C9. 若点 在一次函数 的图象上，则点 一定不在（ ）A、第一象限 B、第二象限 C、第三象限 D、第四象限10. 为了研究特殊四边形，刘老师制作了这样一个教具（如图1）：用钉子将四根木条钉成一个平行四边形框架ABCD，并在A与C，B与D两点之间分别用一根橡皮筋拉直固定，课上，刘老师右手拿住木条BC，用左手向右推动框架至AB⊥BC（如图2），观察所得到的四边形，下列结论：①∠BCA＝45°；②AC的长度变小；③AC＝BD；④AC⊥BD.正确的有（ ）
A、1个 B、2个 C、3个 D、4个11. 某休息日，李铁骑自行车从家出发去公园，在公园停留了一段时间后，发现自行车车胎损坏，于是推车原路返回，途经某自行车修理店，停下来修车，修好车后骑车回家.图中x表示时间，y表示李铁离家的距离，依据图中的信息，下列说法错误的是（ ）
A、李铁从公园回家用时1.5h B、公园离李铁家6000m C、李铁推车的平均速度是2km/h D、李铁修好车后骑车回家的平均速度是12km/h12. 如图，在正方形ABCD中，取AD的中点E，连接EB，延长DA至F，使EF＝EB，以线段AF为边作正方形AFGH，交AB于点H，则 的值是（ ）
A、 B、 C、 D、二、填空题
-
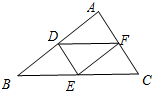
13. 某人调查25个人对某种商品是否满意，结果有15人满意，有5人不满意，有5人不好说，则满意的频率为14. 正九边形的每一个内角是度.15. 如图，D，E，F分别为△ABC三边的中点，则图中平行四边形的个数为.
16. 如图，正比例函数y=﹣x的图象与一次函数y=kx+ （k≠0）的图象相交于点P，则关于x的方程﹣x=kx+ 的解是.
17. 如图，以Rt△ABC的三边为直角边分别向外作等腰直角三角形.若AB= ，则图中阴影部分的面积为.
18. 过△ABC的顶点C画线段CD，使得线段CD与AB边平行且相等，则下列说法：①若∠BAC=90°，则以A，B，C，D为顶点的四边形是矩形；
②若以A，B，C，D为顶点的四边形是矩形，则∠BAC=90°；
③若AB=AC=BC，则以A，B，C，D为顶点的四边形是菱形；
④若以A，B，C，D为顶点的四边形是菱形，则AB=AC.
其中正确的说法有个.
三、解答题
-
19. 已知y与2x﹣1成正比例，当x＝3时，y＝10，求y与x之间的函数关系式.20. 如图，点B、E分别在AC、DF上，AF分别交BD、CE于点M、N，∠A＝∠F，∠C＝∠D.
(1)、求证：四边形BCED是平行四边形；(2)、已知DE＝3，连接BN，若BN平分∠DBC，求CN的长.21. 如图，在正方形ABCD中，F为DC的中点，E为BC上一点，且CE= BC，连接AE，求证：△AFE是直角三角形.
22. 如图，在平面直角坐标系中，已知△ABC的三个顶点的坐标分别为A(-3，5)，B(-2，1)，C(-1，3).
( 1 )画出△ABC关于x轴的对称图形△A1B1C1；
( 2 )画出△A1B1C1沿x轴向右平移4个单位长度后得到的△A2B2C2；
( 3 )如果AC上有一点M(a，b)经过上述两次变换，那么对应A2C2上的点M2的坐标是_▲_.
23. 今年是建党100周年，某校团委组织全校3000名学生参加了党史知识竞赛.为了解本次大赛的成绩，校团委随机抽取了其中200名学生的成绩（成绩取整数，满分100分）作为样本进行统计，制成不完整的统计图表.
成绩x/分
频数
频率
50≤x＜60
m
0.08
60≤x＜70
40
0.20
70≤x＜80
a
n
80≤x＜90
56
0.28
90≤x＜100
24
0.12
根据所给信息，解答下列问题：
(1)、m= ， n= ， a=.(2)、表中组距是分，组数是组.(3)、补全频数分布直方图.(4)、这200名学生成绩的中位数会落在分数段.24. 如图，△ABC中，∠ACB=90°，AB=5cm，BC=3cm，若点P从点A出发，以每秒2cm的速度沿折线A﹣C﹣B﹣A运动，设运动时间为t秒（t＞0）.
(1)、填空：AC=.(2)、若点P在AC上，且满足PA=PB时，求出此时t的值.(3)、若点P恰好在∠BAC的角平分线上（不与A点重合），求t的值.25. 如图，在平面直角坐标系xOy中，已知一次函数y=﹣2x＋4的图象与x轴相交于点A，与y轴相交于点B.
(1)、求点A坐标和点B坐标；(2)、点C是线段AB上一点，点O为坐标原点，点D在第二象限，且四边形BCOD为菱形，求点D坐标；(3)、在（2）的条件下，点P为平面直角坐标系中一点，以B、D、A、P为顶点的四边形是平行四边形，请直接写出所有满足条件的P点坐标.26. 如图，在矩形ABCD中，E是AD的中点，将△ABE沿BE折叠，点A的对应点为点F.
(1)、如图1，当点F恰好落在BC边上时，判断四边形ABFE的形状，并说明理由.(2)、如图2，当点F在矩形ABCD内部时，延长BF交DC边于点G.①试探究线段BG，AB，DG之间的数量关系，并说明理由.
②当G点分CD边的比为1：3时，试探究矩形ABCD的边长AD和AB之间的数量关系，并说明理由.