福建省泉州市南安市2020-2021学年八年级下学期数学期末考试试卷

试卷更新日期：2021-08-17 类型：期末考试

进入出卷网下载

一、单选题

1. 要使分式 $\frac{2}{x -1}$ 有意义， $x$ 必须满足的条件是（）

A、 $x \neq 0$ B、 $x \neq 1$ C、 $x < 1$ D、 $x > 1$

查看试题解析
2. 在平面直角坐标系中，点 $A (2 ， - 3)$ 位于（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
3. 若一次函数 $y = 2 x + b$ 的图象经过点 $(2 ， 3)$ ，则 $b$ 的值是（）

A、-1 B、1 C、5 D、7

查看试题解析
4. 2020年6月23日9时43分，我国成功发射了北斗系统第55颗导航卫星，其授时精度为世界之最，不超过0.0000000099秒.数据“0.0000000099”用科学记数法表示为（）

A、 $99 \times 10^{- 10}$ B、 $9.9 \times 10^{- 10}$ C、 $9.9 \times 10^{- 9}$ D、 $0.99 \times 10^{- 8}$

查看试题解析
5. 某校足球队有16名队员，队员的年龄情况统计如下：

年龄 $/$ 岁

13

14

15

16

人数

3

5

6

2

则这16名队员年龄的众数是（）

A、5 B、6 C、14 D、15

查看试题解析
6. 如图，在四边形ABCD中，对角线AC和BD相交于点O ，下列条件不能判断四边形ABCD是平行四边形的是（）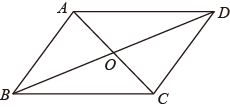

A、 $A B / / D C$ ， $A D / / B C$ B、 $A B = D C$ ， $A D = B C$ C、 $A B / / D C$ ， $A D = B C$ D、 $O A = O C$ ， $O B = O D$

查看试题解析
7. 一组数据的方差可以用式子 $s^{2} = \frac{{(x_{1} - 40)}^{2} + {(x_{2} - 40)}^{2} + {(x_{3} - 40)}^{2} + \dots + {(x_{10} - 40)}^{2}}{10}$ 表示，则式子中的数40所表示的意义是（）

A、这组数据的个数 B、这组数据的平均数 C、这组数据的众数 D、这组数据的中位数

查看试题解析
8. 甲，乙两个工程队，甲队修路 $600$ 米与乙队修路 $800$ 米所用的时间相等，乙队每天比甲队多修 $20$ 米.若可列方程 $\frac{600}{x} = \frac{800}{x + 20}$ 表示题中的等量关系，则方程中 $x$ 表示（）

A、甲队每天修路的长度 B、乙队每天修路的长度 C、甲队修路 $300$ 米所用天数 D、乙队修路 $400$ 米所用天数

查看试题解析
9. 如图，在矩形ABCD中，AB=4，AD=6，点P在AD上，点Q在BC上，且AP = CQ，连接CP，QD，则PC + QD的最小值为（）

A、8 B、10 C、12 D、20

查看试题解析
10. 如图，在正方形 $A B C D$ 外取一点 $E$ ，连接 $A E$ ， $B E$ ， $D E$ .过点 $A$ 作 $A E$ 的垂线交 $D E$ 于点 $P$ .若 $A E = A P = 1$ ， $P B = \sqrt{10}$ ，下列结论：① $Δ A P D$ ≌ $Δ A E B$ ； ②点 $B$ 到直线 $A E$ 的距离为 $2$ ；③ $B P = P D$ ； ④ $S_{Δ A P D} + S_{Δ A P B} = \frac{5}{2}$ .其中正确结论的序号是（）

A、①③④ B、①②③ C、②③④ D、①②④

查看试题解析

二、填空题

11. 计算： $\frac{a}{a + 1} + \frac{1}{a + 1}$ ＝

查看试题解析
12. 若一次函数 $y = - 5 x + b$ 的图象经过第一、二、四象限，则b0（填“＞”或“＜”）.

查看试题解析
13. 甲、乙两名同学参加“古诗词大赛”活动，五次比赛成绩的平均分都是85分，若两人比赛成绩的方差分别为 $S_{甲}^{2} = 1. 25$ 和 $S_{^{乙}}^{2} = 3$ ，则成绩比较稳定的是（填甲或乙）.

查看试题解析
14. 如图，▱ABCD中，AC、BD相交于点O，若AD=6，AC+BD=16，则△BOC的周长为.

查看试题解析
15. 如图，在 ▱ ABCD中，尺规作图：以点A为圆心，AB的长为半径画弧交AD于点F，分别以点B，F为圆心，以大于BF的长为半径画弧交于点P，作射线AP交BC与点E，若BF = 12，AB = 10，则AE的长为.

查看试题解析
16. 如图，已知在平面直角坐标系 $x O y$ 中， $Rt Δ O A B$ 的直角顶点 $B$ 在 $x$ 轴的正半轴上，点 $A$ 在第一象限，反比例函数 $y = \frac{k}{x} (x > 0)$ 的图象经过 $O A$ 的中点 $C$ .交 $A B$ 于点 $D$ ，连接 $C D$ .若 $Δ A C D$ 的面积是3，则四边形 $O B D C$ 的面积是.

查看试题解析

三、解答题

17. 计算： ${(π - 3.1)}^{0} - {(\frac{1}{2})}^{- 2} + \sqrt{9}$

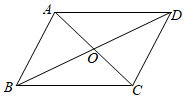
查看试题解析
18. 先化简，再求值：(x + $\frac{2 x + 1}{x}$ )÷(x+1)，其中x=3.

查看试题解析
19. 如图，四边形ABCD中，AD∥BC ，AC、BD相交于点O，O是AC的中点.
求证：四边形ABCD是平行四边形.

查看试题解析
20. 如图，直线 $y_{1} = k x + b$ （ $k$ 为常数， $k \neq 0)$ 与双曲线 $y_{2} = \frac{2}{x}$ 交于 $A$ ， $D$ 两点，与 $x$ 轴、 $y$ 轴分别交于 $B$ ， $C$ 两点，点 $A$ 的坐标为 $(m ， 2)$ ，点 $D$ 的坐标为 $(- 2 ， n)$ .

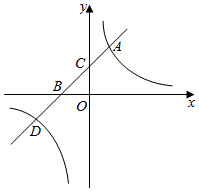(1)、求直线的解析式.

(2)、结合图象直接写出当 $y_{1} < y_{2}$ 时， $x$ 的取值范围.

查看试题解析
21. 如图，在□ $A B C D$ 中， $∠ A B C = 135 °$ .

(1)、尺规作图：在 $B C$ 边上求作点 $P$ ，使得 $∠ P D C = 45 °$ （保留作图痕迹，不写作法）

(2)、若 $A B = 6 \sqrt{2}$ ， $A D = 8$ ，求□ $A B C D$ 的面积.

查看试题解析

22. 随着生活节奏的加快以及智能手机的普及，外卖点餐逐渐成为越来越多用户的餐饮消费习惯.由此催生了一批外卖点餐平台，已知某外卖平台的送餐费用与送餐距离有关（该平台只给5千米范围内配送），为调查送餐员的送餐收入，现从该平台随机抽取80名点外卖的用户进行统计，按送餐距离分类统计结果如下表：

送餐距离x（千米）	0＜x ≤1	1＜x ≤2	2＜x ≤3	3＜x ≤4	4＜x ≤5
数量（份）	12	20	24	16	8

(1)、设这80名点外卖的用户送餐距离的中位数为m（千米），则m的取值范围是（）

A、1＜m ≤ 2 B、2＜m ≤ 3 C、3＜m ≤ 4 D、4＜m ≤ 5

(2)、以这80名点外卖用户的送餐距离为研究对象，同一组数据取该小组数据的中间值（例如小组（1＜x ≤ 2）的中间值是1.5），计算这80名点餐用户的平均送餐距离；

(3)、若该外卖平台给送餐员的送餐费用与送餐距离有关，不超过2千米时，每份3元；超过2千米但不超4千米时，每份5元；超过4千米时，每份9元.以给这80名用户所需送餐费用的平均数为依据，若送餐员一天的目标收入不低于200元，试估计一天至少要送多少份外卖？

查看试题解析

23. 某鞋厂准备生产A，B两种品牌运动鞋共100万双，已知生产每双A种品牌和B种品牌运动鞋共需成本215元，且每双B种品牌运动鞋成本比A种高15元.

(1)、求A，B两种品牌运动鞋每双的成本分别是多少元；

(2)、“百年大计，教育为本”，该鞋厂主动扛起支持地方教育发展的使命，每售出1双A种品牌运动鞋就捐出a元来支持地方政府进行助学、奖学.根据市场供需情况，计划生产A种品牌运动鞋至少60万双，B种品牌运动鞋至少20万双.已知A，B两种品牌运动鞋每双售价分别为130元和140元，该鞋厂将如何安排生产才能获得最大利润，最大利润是多少万元？（注：利润＝（销售收入）－（成本）－（捐款））

查看试题解析
24. 在平面直角坐标系中，矩形 $O A B C$ 的顶点 $A$ ， $C$ 分别在 $x$ 轴、 $y$ 轴上，将矩形 $A B C O$ 绕点 $O$ 顺时针旋转角α得到矩形 $D E F O$ ，点 $A$ 、 $B$ 、 $C$ 的对应点分别为 $D$ 、 $E$ 、 $F$ .

(1)、如图1，当 $D E$ 过点C时，且 $B$ 的坐标为 $(- 3 ， 5)$ .求 $D C$ 的长；

(2)、如图2，当点 $D$ 落在AC上时，连结 $C E$ 、 $O E$ .
① 四边形 $O A C E$ 是何特殊的四边形？请说明理由；

② 证明点 $B$ 、 $C$ 、 $E$ 三点共线.

查看试题解析
25. 如图1，直线 $y_{1} = 2 x + 6$ 分别交 $x$ 轴、 $y$ 轴于 $A$ ， $B$ 两点.

(1)、直接写出 $A$ 、 $B$ 两点的坐标；

(2)、如图2，已知直线 $y_{2} = k x - 6 k + 3$ ，无论k取何值，它都经过第一象限内的一个定点 $C$ ，分别连结 $A C$ 、 $B C$ ，其中 $A C$ 交 $y$ 轴于 $D$ 点.
① 求 $Δ A B D$ 的面积；

② 连接 $O C$ ，在直线 $O C$ 上是否存在着点 $P$ ，使得 $S_{Δ P A B} = \frac{1}{3} S_{Δ A B C}$ ？若存在，请直接写出 $P$ 点的坐标（不写求解过程）；若不存在，请说明理由.

查看试题解析

年龄 $/$ 岁	13	14	15	16
人数	3	5	6	2