福建省泉州市安溪县2020-2021学年八年级下学期数学期末考试试卷

试卷更新日期：2021-08-17 类型：期末考试

进入出卷网下载

一、单选题

1. 分式 $\frac{2}{x - 2}$ 在实数范围内有意义，则x的取值范围是（）

A、 $x > 2$ B、 $x < 2$ C、 $x = 2$ D、 $x \neq 2$

查看试题解析
2. 计算 $\frac{2 m}{m - 2} - \frac{4}{m - 2}$ 的结果是（）

A、1 B、﹣2 C、2 D、﹣1

查看试题解析
3. 一家工艺品厂按计件方式结算工资.小鹿去这家工艺品厂打工，第一天工资60元，第二天比第一天多做了5件，工资为75元.设小鹿第一天做了 $x$ 件，根据题意可列出方程为（）

A、 $\frac{60}{x} = \frac{75}{x + 5}$ B、 $\frac{60}{x - 5} = \frac{75}{x}$ C、 $\frac{75}{x} = \frac{60}{x + 5}$ D、 $\frac{75}{x} = \frac{60}{x} + 5$

查看试题解析
4. 如图，在同一直角坐标系中作出一次函数 $y = k_{1} x$ 与 $y = k_{2} x + b$ 的图象，则二元一次方程组 ${\begin{array}{l} y = k_{2} x + b \\ y = k_{1} x \end{array}$ 的解是（）

A、 ${\begin{array}{l} x = - 3 \\ y = 0 \end{array}$ B、 ${\begin{array}{l} x = 1 \\ y = 3 \end{array}$ C、 ${\begin{array}{l} x = 0 \\ y = 3 \end{array}$ D、 ${\begin{array}{l} x = 1 \\ y = 0 \end{array}$

查看试题解析
5. 关于反比例函数 $y = - \frac{4}{x}$ ，下列说法正确的是（）

A、当 $x > 0$ 时，函数值 $y < 0$ B、y随x的增大而增大 C、点 $(1 ， 4)$ 在该函数图象上 D、图象在一、三象限内

查看试题解析
6. 已知一组数据x₁ ， x₂ ， x₃的平均数为7，则3x₁+2，3x₂+2，3x₃+2的平均数为（）

A、7 B、9 C、21 D、23

查看试题解析
7. 在平面直角坐标系中，点P(a﹣1，a+1)在y轴上，则a的值是（）

A、0 B、1 C、﹣1 D、2

查看试题解析
8. 如图，在四边形ABCD中，对角线AC和BD相交于点O ，下列条件不能判断四边形ABCD是平行四边形的是（）

A、 $A B / / D C$ ， $A D / / B C$ B、 $A B = D C$ ， $A D = B C$ C、 $A B / / D C$ ， $A D = B C$ D、 $O A = O C$ ， $O B = O D$

查看试题解析
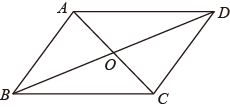9. 下列说法错误的是（）

A、平行四边形对边相等 B、对角线相等的平行四边形是矩形 C、对角线互相垂直的四边形是菱形 D、正方形既是轴对称图形，又是中心对称图形

查看试题解析
10. 如图，矩形ABCD对角线AC、BD相交于点O，点P是AD边上的一个动点，过点P分别作PE⊥AC于点E、PE⊥BD于点F，若AB＝6，BC＝8，则PE+PF的值为（）

A、19.2 B、9.6 C、6 D、4.8

查看试题解析

二、填空题

11. 已知空气的单位体积质量是0.00123g/cm³，把0.00123用科学记数法表示为.

查看试题解析
12. 若分式 $\frac{x - 3}{x + 3}$ 的值为0，则x的值为；

查看试题解析
13. 反比例函数 $y = \frac{k}{x} (k \neq 0)$ 的图像经过点 $A (- 2 ， 3) ， B (1 ， m)$ ，则m的值为.

查看试题解析
14. 菱形的两条对角线分别为8、10，则菱形的面积为.

查看试题解析
15. 若关于x的分式方程 $\frac{3 x}{x - 2} = \frac{m}{2 - x} +$ 4有增根，则m的值为.

查看试题解析
16. 如图，平行于y轴的直线分别交y $= \frac{3}{x}$ （x＞0）与y $= - \frac{2}{x}$ （x＞0）的图像于点A、B，点C是y轴上的动点，则 $△ A B C$ 的面积为.

查看试题解析

三、解答题

17. 计算：15×3^﹣1 $- {(\sqrt{3} - 1)}^{0} +$ （﹣1）²⁰²¹.

查看试题解析
18. 先化简，再求值：（1 $- \frac{a}{a - 3}$ ） $\div \frac{a^{2} + 3 a}{a^{2} - 9}$ .其中a＝﹣6.

查看试题解析
19. 如图，在△ABC中，D是AB边上任意一点，E是BC边中点，CF∥AB，交DE的延长线于点F，连接BF，CD.求证：四边形CDBF是平行四边形.

查看试题解析
20. 已知：如图，正比例函数 $y_{1} = \frac{3}{2} x$ 的图像与反比例函数 $y_{2} = \frac{k}{x}$ 的图像相交于点A和点C，点A的坐标为(2，n).

(1)、求k与n的值.

(2)、试利用函数图象，直接写出当x取何值时，y₁＜y₂.

查看试题解析
21. 某中学八（1）班共50名同学开展了“我为灾区献爱心”捐款活动.小聪将捐款情况进行了统计，并绘制成如下的条形统计图.

(1)、填空：该班同学捐款数额的众数是元，中位数是元；

(2)、该班平均每人捐款多少元？

查看试题解析
22. 我们给出如下定义：如图1，平面内两条直线l₁、l₂ ，相交于点O，对于平面内的任意一点M，若p、q分别是点M到直线l₁和l₂的距离（p≥0，q≥0），称有序非负实数对[p，q]是点M的“距离坐标“.根据上述定义，请解答下列问题：如图2，在平面直角坐标系xOy内，直线l₁的关系式为y＝x，直线l₂的关系式为y $= \frac{1}{3}$ x，M是平面直角坐标系内的点.

(1)、若p＝q＝0，直接写出“距离坐标”为[0，0]时，点M的坐标( ， ).

(2)、若q＝0，且p+q＝m（m＞0），利用图2，在第一象限内，求“距离坐标”为[p，q]时，点M的坐标（用含m的式子表示）.

查看试题解析
23. 为加强“新型冠状病毒”防控，某小区居委会计划购买甲、乙两种品牌的消毒液，乙品牌消毒液的单价比甲品牌消毒液的单价的2倍少10元，已知用300元购买甲品牌消毒液的数量和用450元购买乙品牌消毒液的数量相同，设甲品牌消毒液的单价为每瓶x元.

(1)、直接写出购买乙品牌消毒液的数量：瓶（用含x的代数式表示）；

(2)、求甲、乙两种品牌消毒液的单价各是多少元？

(3)、若该小区居委会从超市一次性购买甲、乙两种品牌的消毒液共50瓶，且总费用不超过1200元，那么至少要购买甲消毒液多少瓶？

查看试题解析
24. 在正方形ABCD中，AB＝2 $\sqrt{2}$ ，O为对角线AC、BD的交点.

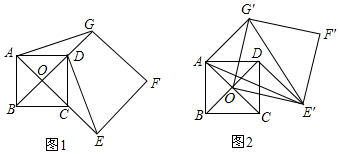(1)、如图1，延长OC，使CE＝OC作正方形OEFG，使点G落在OD的延长线上，连接DE、AG.求证：DE＝AG；

(2)、如图2，将（1）中的正方形OEFG绕点O逆时针旋转α角（0°＜α＜180°）得到正方形 $O E' F' G'$ ，连接 $A E'$ ， $E' G'$ .
①当 $G' A$ ⊥AC时，求 $△ A E' G'$ 的面积；

②在旋转过程中，直接写出 $△ A E' G'$ 面积的最小值，并写出此时旋转角α等于多少度？

查看试题解析
25. 如图，在平面直角坐标系中，直线l：y＝kx+b分别与x轴、y轴相交于点A、B.现将直线l绕原点O顺时针旋转90°，得到的直线 $l ’$ 称为直线l的“顺旋转垂线”.

(1)、若点A、B的坐标分别为A(2，0)、B(0，2)，则直线l的“顺旋转垂线” $l ’$ 的关系式为.

(2)、若直线l＝k₁x+b₁（k₁＜0，b₁≠0）的“顺旋转垂线” $l ’$ 为：y＝k₂x+b₂.求证：k₁•k₂＝﹣1.

(3)、已知直线l的“顺旋转垂线”为l'：y $= \frac{1}{4}$ x+2，点C是直线l与x轴、y轴交点A、B的中点，动点M的坐标为(0，m).问当m为何值时，MA+MC取得最小值，并求出该最小值.

查看试题解析