重庆市潼南区2020-2021学年七年级下学期数学期末考试试卷
试卷更新日期:2021-08-17 类型:期末考试
一、单选题
-
1. 在下列所示的四个汽车标志图案中,其中可以看作由“基本图案”经过平移得到的是( )A、
 B、
B、 C、
C、 D、
D、 2. 在平面直角坐标系中,已知点P(﹣2,3),则点P在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限3. 下列调查中,适合用全面调查方式的是( )A、了解某班学生的身高情况 B、了解一批灯泡的使用寿命 C、了解目前中学生的睡眠情况 D、了解一批炮弹的杀伤半径4. 在下列实数: 、 、 、 、 …(相连两个1之间依次多一个0)中,无理数有( )A、1个 B、2个 C、3个 D、4个5. 下列命题中,真命题是( )A、同位角相等 B、两点之间直线最短 C、同旁内角相等,两直线平行 D、平行于同一条直线的两条直线平行6. 不等式2x+3≥5的解集在数轴上表示正确的是( )
2. 在平面直角坐标系中,已知点P(﹣2,3),则点P在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限3. 下列调查中,适合用全面调查方式的是( )A、了解某班学生的身高情况 B、了解一批灯泡的使用寿命 C、了解目前中学生的睡眠情况 D、了解一批炮弹的杀伤半径4. 在下列实数: 、 、 、 、 …(相连两个1之间依次多一个0)中,无理数有( )A、1个 B、2个 C、3个 D、4个5. 下列命题中,真命题是( )A、同位角相等 B、两点之间直线最短 C、同旁内角相等,两直线平行 D、平行于同一条直线的两条直线平行6. 不等式2x+3≥5的解集在数轴上表示正确的是( )
A、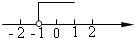 B、
B、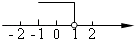 C、
C、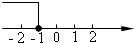 D、
D、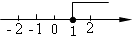 7. 如图,下列条件中能判断 的是( )
7. 如图,下列条件中能判断 的是( )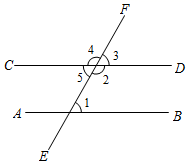 A、 B、 C、 D、8.
A、 B、 C、 D、8.下列图形都是由圆和几个黑色围棋子按一定规律组成,图①中有4个黑色棋子,图②中有7个黑色棋子,图③中有10个黑色棋子,…,依次规律,图⑨中黑色棋子的个数是( )
 A、23 B、25 C、26 D、289. 《九章算术》是中国传统数学最重要的著作,奠定了中国传统数学的基本框架.它的代数成就主要包括开方术、正负术和方程术.其中,方程术是《九章算术》最高的数学成就.《九章算术》中记载:“今有牛五、羊二,直金十两;牛二、羊五,直金八两.
A、23 B、25 C、26 D、289. 《九章算术》是中国传统数学最重要的著作,奠定了中国传统数学的基本框架.它的代数成就主要包括开方术、正负术和方程术.其中,方程术是《九章算术》最高的数学成就.《九章算术》中记载:“今有牛五、羊二,直金十两;牛二、羊五,直金八两.问:牛、羊各直金几何?”
译文:“假设有5头牛、2只羊,值金10两;2头牛、5只羊,值金8两.问:每头牛、
每只羊各值金多少两?”设每头牛值金x两,每只羊值金y两,可列方程组为( )
A、 B、 C、 D、10. 按如图所示的程序计算,若开始输入的x的值是64,则输出的y的值是( ) A、 B、 C、2 D、311. 关于x的方程 的解为非负数,且关于x的不等式组 有解,则符合条件的整数k的值的和为( )A、4 B、5 C、2 D、312. 已知关于x,y的方程组 ,当这个方程组的解x、y满足 ,如果三角形 的顶点坐标分别 , , ,那么三角形 面积的最大值( )A、3 B、6 C、12 D、24
A、 B、 C、2 D、311. 关于x的方程 的解为非负数,且关于x的不等式组 有解,则符合条件的整数k的值的和为( )A、4 B、5 C、2 D、312. 已知关于x,y的方程组 ,当这个方程组的解x、y满足 ,如果三角形 的顶点坐标分别 , , ,那么三角形 面积的最大值( )A、3 B、6 C、12 D、24二、填空题
-
13. 计算: .14. 七年级一班的小明根据本学期“从数据谈节水”的课题学习,知道了统计调查活动要经历5个重要步骤:①收集数据;②设计调查问卷;③用样本估计总体;④整理数据;⑤分析数据.但他对这5个步骤的排序不对,请你帮他正确排序为 .(填序号)15. 如图, , 平分 .若 ,则 的度数为.
 16. 如图将长方形纸片 沿直线 折叠,点A、B分别对应点E、F,再将折叠后的四边形 沿着射线 的方向平移,点F恰好与点C重合后停止,平移后的四边形为四边形 ,要使 ,则 的度数为.
16. 如图将长方形纸片 沿直线 折叠,点A、B分别对应点E、F,再将折叠后的四边形 沿着射线 的方向平移,点F恰好与点C重合后停止,平移后的四边形为四边形 ,要使 ,则 的度数为.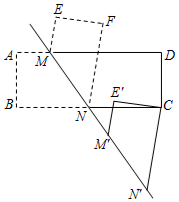 17. 对x、y定义一种新运算T.规定: (m,n均为非零常数).例如: .如果 , .那么 .18. 某地下停车场有5个出入口,每天早晨6点开始对外停车且此时车位空置率为 ,在每个出入口的车辆数均是匀速出入的情况下,如果开放2个进口和3个出口,8小时车库恰好停满;如果开放3个进口和2个出口,2小时车库恰好停满.今年元旦节,由于商场人数增多,早晨6点时的车位空置率变为 ,又因为车库改造,只能开放2个进口和1个出口,则从早晨6点开始经过小时车库恰好停满.
17. 对x、y定义一种新运算T.规定: (m,n均为非零常数).例如: .如果 , .那么 .18. 某地下停车场有5个出入口,每天早晨6点开始对外停车且此时车位空置率为 ,在每个出入口的车辆数均是匀速出入的情况下,如果开放2个进口和3个出口,8小时车库恰好停满;如果开放3个进口和2个出口,2小时车库恰好停满.今年元旦节,由于商场人数增多,早晨6点时的车位空置率变为 ,又因为车库改造,只能开放2个进口和1个出口,则从早晨6点开始经过小时车库恰好停满.三、解答题
-
19. 解下列方程组:(1)、(2)、20. 解不等式(组):(1)、解不等式(2)、解不等式组:21. 某校为了了解初三年级800名学生的身体健康情况,从该年级随机抽取了若干名学生,将他们按体重(均取整数,单位: )分成五组(A:39.5~46.5;B:46.5~53.5;C:53.5~60.5;D:60.5~67.5;E:67.5~74.5),并依据统计数据绘制了如下两幅尚不完整的统计图.

根据统计图,解答下列问题:
(1)、这次抽样调查的样本容量是 , 并补全频数分布直方图;
(2)、D组学生的频率为 , 在扇形统计图中E组的圆心角是度;(3)、请你估计该校初三年级体重低于 的学生大约有多少名?22. 如图, , , (1)、若 ,求 的度数(2)、求证:23. 某小区绿化一块闲置空地,购买了甲、乙两种树木共72棵,其中甲种树木每棵90元,乙种树木每棵80元,共用去资金6160元(1)、求甲、乙两种树木各购买了多少棵?(2)、经过一段时间后,种植的这批树木成活率高,绿化效果好.该小区决定再购买一批这两种树木绿化另一块闲置空地,两种树木的购买数量均与第一批相同,购买时发现甲种树木单价上涨了 ,乙种树木单价下降了 ,且总费用不超过6804元,求a的最大值.24. 如图,在正方形网格中,每个小正方形的边长为1个单位长度,格点 (顶点是网格的交点的三角形)的顶点A,C坐标分别为 ,
(1)、若 ,求 的度数(2)、求证:23. 某小区绿化一块闲置空地,购买了甲、乙两种树木共72棵,其中甲种树木每棵90元,乙种树木每棵80元,共用去资金6160元(1)、求甲、乙两种树木各购买了多少棵?(2)、经过一段时间后,种植的这批树木成活率高,绿化效果好.该小区决定再购买一批这两种树木绿化另一块闲置空地,两种树木的购买数量均与第一批相同,购买时发现甲种树木单价上涨了 ,乙种树木单价下降了 ,且总费用不超过6804元,求a的最大值.24. 如图,在正方形网格中,每个小正方形的边长为1个单位长度,格点 (顶点是网格的交点的三角形)的顶点A,C坐标分别为 , (1)、①请在如图所示的网格内画出对应的平面直角坐标系;
(1)、①请在如图所示的网格内画出对应的平面直角坐标系;
②再把 先向右平移5个单位长度,再向下平移3个单位长度得到 ,且点 的对应点分别为 ,请你在图中画出 ;(2)、在Y轴上是否存在点P,使 的面积等于 的面积的一半,若存在求出点P的坐标;若不存在说明理由.25. 定义:两个数位相同的自然数,如果将一个自然数的各数字逆向排列后变成另一个自然数(可以等于它本身),那么我们把这样的两个自然数互称为“逆数”.例如:456、73、88的“逆数”分别是654、37、88(1)、求证:任意三位数 与其“逆数”之差一定能被99整除;(2)、设两位数 减去其“逆数”所得的差是一个完全平方数.求出满足条件的所有两位数的个数.(词义解读(1)一个数的逆数可以等于它本身,比如88的逆数也是88;(2)三位数 中a表示百位数字,b表示十位数字,c表示个位数字;两位数 中x表示十位数字,y表示个位数字;(3)完全平方数:如 , , ……,我们称0、1、4……叫完全平方数.)
26. 问题情境:如图1, , , ,求 的度数.小明的思路是:过P作 ,通过平行线性质来求 .
 (1)、按小明的思路,易求得 的度数为度:(直接写出答案)(2)、问题迁移:如图2, ,点P在射线 上运动,记 , ,当点P在B、D两点之间运动时,问 与 、 之间有何数量关系?请说明理由;(3)、在(2)的条件下,如果点P在B、D两点外侧运动时(点P与点O、B、D三点不重合),请直接写出 与 、 之间的数量关系.
(1)、按小明的思路,易求得 的度数为度:(直接写出答案)(2)、问题迁移:如图2, ,点P在射线 上运动,记 , ,当点P在B、D两点之间运动时,问 与 、 之间有何数量关系?请说明理由;(3)、在(2)的条件下,如果点P在B、D两点外侧运动时(点P与点O、B、D三点不重合),请直接写出 与 、 之间的数量关系.