重庆市缙云教育联盟2020-2021学年七年级下学期数学期末考试试卷
试卷更新日期:2021-08-17 类型:期末考试
一、单选题
-
1. 某同学解方程 时,把“ ”处的系数看错了,解得 ,他把“ ”处的系数看成了( )A、4 B、 C、6 D、2. 下列方程中,属于二元一次方程的是( )A、x y B、 C、2x y z D、3. 某品牌自行车的标价比成本价高20% ,根据市场需求,该自行车需降价x% ,若保证不亏本,则x应满足( )A、x≤ B、x≤25 C、x< D、x<4. 已知△ABC中 ,则△ABC一定是( )A、锐角三角形 B、直角三角形 C、钝角三角形 D、不能确定5. 下列关于数字变换的图案中,不是中心对称图形但是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 6. 已知下列方程:① ;② ;③ ;④ ;⑤ ;⑥ 其中一元一次方程的个数是( )A、2 B、3 C、4 D、57. 同型号的甲、乙两辆车加满气体燃料后均可行驶210km,它们各自单独行驶并返回的最远距离是105km,现在它们都从A地出发,行驶途中停下来从甲车的气体燃料桶抽一些气体燃料注入乙车的气体燃料桶,然后甲车再行驶返回A地,而乙车继续行驶,到B地后再行驶返回A地.则B地最远可距离A地( )A、120km B、140km C、160km D、180km8. 将一箱苹果分给若干个小朋友,若每位小朋友分5个苹果,则还剩12个苹果;若每位小朋友分8个苹果,则有一个小朋友分到苹果但不到8个苹果.求这一箱苹果的个数与小朋友的人数.若设有x人,则可列不等式为( )A、 B、 C、 D、9. 如图,AD是 的中线,DE是 的高线, , , ,则点D到AB的距离是( )
6. 已知下列方程:① ;② ;③ ;④ ;⑤ ;⑥ 其中一元一次方程的个数是( )A、2 B、3 C、4 D、57. 同型号的甲、乙两辆车加满气体燃料后均可行驶210km,它们各自单独行驶并返回的最远距离是105km,现在它们都从A地出发,行驶途中停下来从甲车的气体燃料桶抽一些气体燃料注入乙车的气体燃料桶,然后甲车再行驶返回A地,而乙车继续行驶,到B地后再行驶返回A地.则B地最远可距离A地( )A、120km B、140km C、160km D、180km8. 将一箱苹果分给若干个小朋友,若每位小朋友分5个苹果,则还剩12个苹果;若每位小朋友分8个苹果,则有一个小朋友分到苹果但不到8个苹果.求这一箱苹果的个数与小朋友的人数.若设有x人,则可列不等式为( )A、 B、 C、 D、9. 如图,AD是 的中线,DE是 的高线, , , ,则点D到AB的距离是( ) A、11 B、 C、 D、810. 将一张正方形纸片按如图步骤①,②沿虚线对折两次,然后沿③中平行于底边的虚线剪去一个角,展开铺平后的图形是( )
A、11 B、 C、 D、810. 将一张正方形纸片按如图步骤①,②沿虚线对折两次,然后沿③中平行于底边的虚线剪去一个角,展开铺平后的图形是( )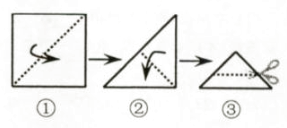 A、
A、 B、
B、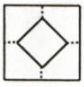 C、
C、 D、
D、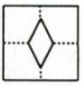 11. 将方程 变形正确的是( )A、 B、 C、 D、
11. 将方程 变形正确的是( )A、 B、 C、 D、二、填空题
-
12. 按如图所示的程序进行计算,如果输入x的值是正整数,输出结果是150,则开始输入x的值可能是.
 13. 若关于x、y的二元一次方程组 ,的解是 ,则关于a、b的二元一次方程组 的解是 .14. 令 a、b 两数中较大的数记作 max|a,b|,如 max|2,3|=3,已知 k 为正整数且使不等式 max|2k+1,﹣k+5|≤5 成立,则 k 的值是.
13. 若关于x、y的二元一次方程组 ,的解是 ,则关于a、b的二元一次方程组 的解是 .14. 令 a、b 两数中较大的数记作 max|a,b|,如 max|2,3|=3,已知 k 为正整数且使不等式 max|2k+1,﹣k+5|≤5 成立,则 k 的值是.三、解答题
-
15. 解方程(1)、(2)、 .16. 为了庆祝建党100周年,某区在文化广场的一块长方形ABCD的空地上,用花卉摆放“100”字样和四个相同的小正方形(如图),其中 米, 米,三个数之间摆放的距离与四个小正方形的边长相等.设小正方形的边长为x米,数字的宽度均为y米.
 (1)、请用关于x,y的代数式表示“0”内部小长方形的长和宽.(2)、若“0”内部小长方形的长和宽分别是 米和 米.
(1)、请用关于x,y的代数式表示“0”内部小长方形的长和宽.(2)、若“0”内部小长方形的长和宽分别是 米和 米.①求x,y的值;
②为了整体美观,将在四个正方形、“100”及“0”的内部小长方形分别摆放甲、乙、丙三种花卉,三种花卉的单价都为整数,其中甲花卉的单价在 元 米 之间 含95和 ,乙、丙两种花卉的单价之和为300元 米 已知三种花卉总价为6200元,则丙花卉的单价是 元/米2.
17. 解不等式请结合题意填空,完成本题的解答.
(Ⅰ)解不等式①,得_▲_;
(Ⅱ)解不等式②,得_▲_;
(Ⅲ)把不等式①和②的解集在数轴上表示出来:

(Ⅳ)原不等式组的解集为▲.
18. 如图,在三角形ABC中, ∠B=60°, ∠C= ,点D是AB上一点,点E是AC上一点, ∠ADE=60°, 点F为线段BC上一点,连接EF,过D作DG//AC交EF于点G,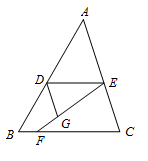 (1)、若 =40°,求∠EDG的度数;(2)、若∠FEC=2∠DEF,∠DGF= ∠BFG,求 .19. 如图,在边长为1的小正方形组成的网格中,给出了格点 .
(1)、若 =40°,求∠EDG的度数;(2)、若∠FEC=2∠DEF,∠DGF= ∠BFG,求 .19. 如图,在边长为1的小正方形组成的网格中,给出了格点 .
( 1 )将 先向下平移3个单位长度,再向右平移4个单位长度得到 ,画出平移后的图形;
( 2 )将 绕点 逆时针旋转 后得到 ,画出旋转后的图形.
20. 阅读下列材料:问题:怎样将 表示成分数?
小明的探究过程如下:
设 ① ②
③ ④
⑤ ⑥
⑦
根据以上信息,回答下列问题:
(1)、从步骤①到步骤②,变形的依据是;从步骤⑤到步骤⑥,变形的依据是;(2)、仿照上述探求过程,请你将 表示成分数的形式.21. 如图1,直角三角形DEF与直角三角形ABC的斜边在同一直线上, , , 如图2,连接CD,CD平分 ,将 绕点D按逆时针方向旋转,记 为 .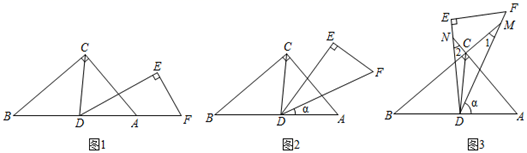 (1)、 的度数为 .(2)、如图3,在旋转过程中,当顶点C在 内部时,边DF,DE分别交BC,AC的延长线于点M,N.
(1)、 的度数为 .(2)、如图3,在旋转过程中,当顶点C在 内部时,边DF,DE分别交BC,AC的延长线于点M,N.①求 的度数范围;
② 与 度数的和是否变化?若不变,请求出 与 的度数和;若变化,请说明理由.