重庆市江津区2020-2021学年七年级下学期数学期末考试试卷
试卷更新日期:2021-08-17 类型:期末考试
一、单选题
-
1. 如图 与 不是对顶角的是( )A、
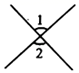 B、
B、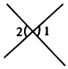 C、
C、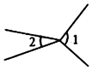 D、
D、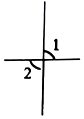 2. 下列各数中,是无理数的是( )A、 B、 C、 D、1.232333. 在平面直角坐标系中,点 位于( )A、第一象限 B、第二象限 C、第三象限 D、第四象限4. 不等式 的解集在数轴上表示正确的是( )A、
2. 下列各数中,是无理数的是( )A、 B、 C、 D、1.232333. 在平面直角坐标系中,点 位于( )A、第一象限 B、第二象限 C、第三象限 D、第四象限4. 不等式 的解集在数轴上表示正确的是( )A、 B、
B、 C、
C、 D、
D、 5. 下列调查中,最适合采用全面调查方式的是( )A、调查重庆市中学生的视力情况 B、调查长江某段流域的水质情况 C、调查“嫦娥五号”月球探测器零部件的合格情况 D、调查某品牌汽车的抗撞击情况6. 中国清代算书《御制数理精蕴》中有这样一题:“马四匹、牛六头,共价四十八两(我国古代货币单位):马三匹、牛五头,共价三十八两.问马、牛各价几何?”设马每匹价值x两,牛每头y两,根据题意可列方程组为( )A、 B、 C、 D、7. 如图, , , 平分 ,则 的度数等于( )
5. 下列调查中,最适合采用全面调查方式的是( )A、调查重庆市中学生的视力情况 B、调查长江某段流域的水质情况 C、调查“嫦娥五号”月球探测器零部件的合格情况 D、调查某品牌汽车的抗撞击情况6. 中国清代算书《御制数理精蕴》中有这样一题:“马四匹、牛六头,共价四十八两(我国古代货币单位):马三匹、牛五头,共价三十八两.问马、牛各价几何?”设马每匹价值x两,牛每头y两,根据题意可列方程组为( )A、 B、 C、 D、7. 如图, , , 平分 ,则 的度数等于( ) A、 B、 C、 D、8. 若 ,则下列式子中错误的是( )A、 B、 C、 D、9. 如果 ,那么x,y的值为( )A、 B、 C、 D、10. 估计 的值( )A、在7和8之间 B、在6和7之间 C、在5和6之间 D、在3和4之间11. 如图,在平面直角坐标系中,有若干个整数点,其顺序按图中方向排列,如 , , , , , ,…,根据规律探索可得,第51个点的坐标为( )
A、 B、 C、 D、8. 若 ,则下列式子中错误的是( )A、 B、 C、 D、9. 如果 ,那么x,y的值为( )A、 B、 C、 D、10. 估计 的值( )A、在7和8之间 B、在6和7之间 C、在5和6之间 D、在3和4之间11. 如图,在平面直角坐标系中,有若干个整数点,其顺序按图中方向排列,如 , , , , , ,…,根据规律探索可得,第51个点的坐标为( ) A、 B、 C、 D、12. 从 ,0,1,2,3,4,5,6这八个数中,随机抽取一个数记为m,若数m使关于x的不等式组 无解,且使关于x的一元一次方程 有整数解,那么这八个数所有满足条件的m的个数有( )A、1 B、2 C、3 D、4
A、 B、 C、 D、12. 从 ,0,1,2,3,4,5,6这八个数中,随机抽取一个数记为m,若数m使关于x的不等式组 无解,且使关于x的一元一次方程 有整数解,那么这八个数所有满足条件的m的个数有( )A、1 B、2 C、3 D、4二、填空题
-
13. 将一个含 的三角尺和一把直尺按如图所示摆放,若 ,则 .
 14. “x与4的和不小于x的7倍”用不等式表示为.15. 关于x,y的二元一次方程组 的解满足 ,则 .16. 在平面直角坐标系中,已知点 、 、 ,且三角形 的面积等于8,则a的值是.17. 某中学七年级在数学竞赛活动中举行了“一题多解”比赛,按分数高低取前50名获奖,原定一等奖5人,二等奖10人,三等奖35人,现调整为一等奖10人,二等奖15人,三等奖25人,调整后一等奖平均分降低5分,二等奖平均分降低3分,三等奖平均分降低1分,如果原来一等奖比二等奖平均分数多2分,则调整后二等奖比三等奖平均分数多分.
14. “x与4的和不小于x的7倍”用不等式表示为.15. 关于x,y的二元一次方程组 的解满足 ,则 .16. 在平面直角坐标系中,已知点 、 、 ,且三角形 的面积等于8,则a的值是.17. 某中学七年级在数学竞赛活动中举行了“一题多解”比赛,按分数高低取前50名获奖,原定一等奖5人,二等奖10人,三等奖35人,现调整为一等奖10人,二等奖15人,三等奖25人,调整后一等奖平均分降低5分,二等奖平均分降低3分,三等奖平均分降低1分,如果原来一等奖比二等奖平均分数多2分,则调整后二等奖比三等奖平均分数多分.三、解答题
-
18.(1)、计算: ;(2)、解不等式: .19.(1)、解方程组: .(2)、解不等式组: .20. 为庆祝中国共产党成立100周年,让红色基因、革命薪火代代传承,我区开展了以学习“四史”(党史、新中国史、改革开放史、社会主义发展史)为主题的书画展,为了解作品主题分布情况,在学生上交的作品中,随机抽取了50份进行统计,并根据调查统计结果绘制了如下统计图表:
主题
频数
频率
A党史
6
0.12
B新中国史
20
n
C改革开放史
0.18
D社会主义发展史
m
合计
50
1

请结合上述信息完成下列问题:
(1)、 , ;(2)、请补全频数分布直方图;(3)、在扇形统计图中,“社会主义发展史”主题作品份数对应的圆心角是度;(4)、若全区共上交书画作品4000份,根据抽样调查结果,请估计以“党史”为主题的作品份数.21. 如图,在平面直角坐标系中,三角形 的三个顶点分别是 , , .将三角形 先向右平移5个单位,再向下平移4个单位,得到三角形 . (1)、请在图中画出平移后的三角形 ;(2)、直接写出 、 、 的坐标;(3)、三角形 的面积是.22. 如图,已知点E、F在直线 上,点G在线段 上, 与 交于点H, , .
(1)、请在图中画出平移后的三角形 ;(2)、直接写出 、 、 的坐标;(3)、三角形 的面积是.22. 如图,已知点E、F在直线 上,点G在线段 上, 与 交于点H, , .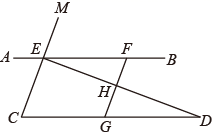 (1)、求证: ;(2)、若 于点H, ,求 的度数.23. 一个四位正整数的千位、百位、十位、个位上的数字分别为a,b,c,d,如果 ,那么我们把这个四位正整数叫做顺次数,例如四位正整数1369:因为 ,所以1369叫做顺次数.(1)、四位正整数中,最大的“顺次数”是 , 最小的“顺次数”是;(2)、已知一个四位正整数的百位、个位上的数字分别是2、7,且这个四位正整数是“顺次数”,同时,这个四位正整数能被7整除,求这个四位正整数.24. 今年5月,青海和云南发生地震.我区民政局将为受灾地区捐赠的物资打包成件,其中帐篷和食品共600件,帐篷比食品多60件.(1)、求打包成件的帐篷和食品各多少件?(2)、现计划租用甲、乙两种货车共12辆,一次性将这批帐篷和食品全部运往受灾地区.已知甲种货车最多可装帐篷35件和食品19件,乙种货车最多可装帐篷和食品各25件.则民政局安排甲、乙两种货车时有几种方案?(3)、在第(2)问的条件下,如果甲种货车每辆需付运输费5000元,乙种货车每辆需付运输费4000元.民政局应选择哪种方案可使运输费最少?最少运输费是多少元?25. 如图1, ,在 、 内有一条折线 .
(1)、求证: ;(2)、若 于点H, ,求 的度数.23. 一个四位正整数的千位、百位、十位、个位上的数字分别为a,b,c,d,如果 ,那么我们把这个四位正整数叫做顺次数,例如四位正整数1369:因为 ,所以1369叫做顺次数.(1)、四位正整数中,最大的“顺次数”是 , 最小的“顺次数”是;(2)、已知一个四位正整数的百位、个位上的数字分别是2、7,且这个四位正整数是“顺次数”,同时,这个四位正整数能被7整除,求这个四位正整数.24. 今年5月,青海和云南发生地震.我区民政局将为受灾地区捐赠的物资打包成件,其中帐篷和食品共600件,帐篷比食品多60件.(1)、求打包成件的帐篷和食品各多少件?(2)、现计划租用甲、乙两种货车共12辆,一次性将这批帐篷和食品全部运往受灾地区.已知甲种货车最多可装帐篷35件和食品19件,乙种货车最多可装帐篷和食品各25件.则民政局安排甲、乙两种货车时有几种方案?(3)、在第(2)问的条件下,如果甲种货车每辆需付运输费5000元,乙种货车每辆需付运输费4000元.民政局应选择哪种方案可使运输费最少?最少运输费是多少元?25. 如图1, ,在 、 内有一条折线 . (1)、求证: ;(2)、如图2,已知 的平分线与 的平分线相交于点Q,且 , ,直接写出 与 的度数;(3)、如图3,已知 , ,则 与 有什么关系,请说明理由.
(1)、求证: ;(2)、如图2,已知 的平分线与 的平分线相交于点Q,且 , ,直接写出 与 的度数;(3)、如图3,已知 , ,则 与 有什么关系,请说明理由.