重庆市江北区2020-2021学年七年级下学期数学期末考试试卷

试卷更新日期：2021-08-17 类型：期末考试

进入出卷网下载

一、单选题

1. 下列各数中不是无理数的是（）

A、 $\sqrt{4}$ B、 $\sqrt{5}$ C、 $\sqrt{6}$ D、 $\sqrt{7}$

查看试题解析
2. 下列采用的调查方式中，合适的是（）

A、为了解嘉陵江的水质情况，采用抽样调查的方式 B、某鞋厂检测生产的鞋底能承受的弯折次数，采用普查的方式 C、某小型企业给在职员工做工作服前进行尺寸大小的调查，采用抽样调查的方式 D、教育部为了解中小学生的视力情况，采用普查的方式

查看试题解析
3. 下列说法正确的是（）

A、8的立方根 $\pm 2$ B、无限小数都是无理数 C、无理数是无限不循环小数 D、立方根等于本身的数是0

查看试题解析
4. 若 $x$ 轴上的点 $M$ 到 $y$ 轴的距离为4，则点 $M$ 的坐标是（）

A、 $(4 ， 0)$ B、 $(4 ， 0)$ 或 $(- 4 ， 0)$ C、 $(0 ， 4)$ D、 $(0 ， 4)$ 或 $(0 ， - 4)$

查看试题解析
5. 不等式组 ${\begin{array}{l} x - 2 > 0 \\ 2 x - 8 \leq 0 \end{array}$ 的解集是（）

A、 $x > 2$ B、 $x \leq 4$ C、 $x < 2$ D、 $2 < x \leq 4$

查看试题解析
6. 若一个多边形的内角和是外角和的1.5倍，则这个多边形是（）

A、三角形 B、四边形 C、五边形 D、六边形

查看试题解析
7. 如图， $∠ 1 = 110 °$ ，要使 $a$ // $b$ ，则 $∠ 2$ 的大小是（）

A、 $60 °$ B、 $80 °$ C、 $110 °$ D、 $120 °$

查看试题解析
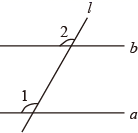8. 如图，一块直角三角尺的一个顶点落在直尺的一边上，若 $∠ 2 = 35^{\circ}$ ，则 $∠ 1$ 的度数为（）

A、45° B、 $55^{\circ}$ C、 $65^{\circ}$ D、 $75^{\circ}$

查看试题解析
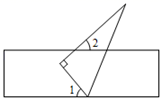9. 已知方程组 ${\begin{matrix} 2 x + y = 3 \\ x - 2 y = 5 \end{matrix}$ ，则2x+6y的值是（）

A、﹣2 B、2 C、﹣4 D、4

查看试题解析
10. 小王网购了一本《好玩的数学》，同学们想知道书的价格，小王让他们猜.喜欢数学的甲同学说：“至少20元.”对数学感觉一般的乙同学说：“至多15元.”讨厌数学的丙同学说：“至多12元.”小王说：“你们三个人都说错了”.则这本书的价格 $x$ （元）所在的范围为（）

A、 $12 < x < 15$ B、 $12 < x < 20$ C、 $15 < x < 20$ D、 $13 < x < 19$

查看试题解析
11. 商店为了对某种商品促销，将定价为30元的商品，以下列方式优惠销售：若购买不超过5件，按原价付款；若一次性购买5件以上，超过部分打八折，现有270元，最多可以购买该商品的件数是（）

A、9件 B、10件 C、11件 D、12件

查看试题解析
12. 若 $m$ 使得关于 $x$ ， $y$ 的二元一次方程组 ${\begin{array}{l} 2 x + y = 3 \\ m x - 2 y = 7 \end{array}$ 有解，且使关于 $x$ 的一元一次不等式组 ${\begin{array}{l} \frac{x - 1}{2} - 2 x \leq 1 \\ 4 x + m \leq 2 \end{array}$ 有且仅有3个整数解，那么所有满足条件的整数 $m$ 的值之和是（）

A、 $- 12$ B、 $- 11$ C、 $- 10$ D、 $- 9$

查看试题解析

二、填空题

13. $2 - \sqrt{5}$ 的相反数是．

查看试题解析
14. 如图，直线 $a$ // $b$ ，直线 $m$ 与 $a$ ， $b$ 均相交，若 $∠ 1 = 36 °$ ，则 $∠ 2 =$ .

查看试题解析
15. 在火车的站台上，有200袋黄豆将被装上火车，袋子的大小都一样，随机选取10袋的质量（单位：kg）分别为：98，100，99，100，99，99，98，98，100，99.估计这200袋黄豆的质量为kg.

查看试题解析
16. 某出租车起步价所包含的路程为 $0 \sim 2 k m$ ，超过 $2 k m$ 的部分按每千米另收费.小江乘坐这种出租车走了 $7 k m$ ，付了16元；小北乘坐这种出租车走了 $13 k m$ ，付了28元.设这种出租车的起步价为 $x$ 元，超过 $2 k m$ 后每千米收费 $y$ 元.根据题意，可列方程组为.

查看试题解析
17. 若点 $P$ 的坐标为 $(\frac{x - 1}{5} ， 2 x - 10)$ ，其中 $x$ 满足不等式组 ${\begin{array}{l} 5 x - 10 \geq 2 (x + 1) \\ \frac{1}{2} x - 1 \leq 7 - \frac{3}{2} x \end{array}$ ，则点 $P$ 在第象限.

查看试题解析
18. 如果两个角的两边两两互相平行，且一个角的 $\frac{1}{n}$ 等于另一角的 $\frac{1}{n + 1}$ （其中 $n$ 为正整数），则这两个角中度数较小的角度为度.（用 $n$ 的代数式表示）

查看试题解析

三、解答题

19. 解方程组：

(1)、 ${\begin{array}{l} 2 x - y = 5 ① \\ 3 x + 2 y = 4 ② \end{array}$ ；

(2)、 ${\begin{array}{l} \frac{1}{3} x - \frac{1}{2} y = 2 \\ 2 (x - 5) + 3 (y - 1) = - 1 \end{array}$ .

查看试题解析
20. 如图， $A B$ // $C D$ ，点 $E$ 是 $C D$ 上一点，

(1)、在 $A B$ 上求作点 $F$ 使得 $A F = A E$ ，并连接 $E F$ ；（按基本作图要求作图，保留作图痕迹，写出结论）

(2)、若 $∠ A E C = 38 °$ ，求 $∠ B F E$ 的度数.（备用知识；两条边相等的三角形为等腰三角形；等腰三角形的两个底角相等，）

查看试题解析
21. 如图，

(1)、写出线段 $A B$ ， $C D$ 有什么位置关系和数量关系；

(2)、求四边形 $A B C D$ 的面积.

(3)、描出 $A (- 3 ， - 2)$ ， $B (2 ， - 1)$ ， $C (3 ， 2)$ ， $D (- 2 ， 1)$ 四个点，并连接， $A B$ ， $B C$ ， $C D$ ， $A D$ .

查看试题解析

22. 争创全国文明城市，从我做起，某学校在七年级开设了文明礼仪校本课程，为了解学生的学习情况，学校随机抽取30名学生进行测试，成绩如下（单位：分）

78 83 86 86 90 94 97 92 89 86 84 81 81 84 86

88 92 89 86 83 81 81 85 86 89 93 93 89 85 93

整理上面的数据得到频数分布表和频数分布直方图：

成绩（分）	频数
$78 \leq x < 82$	5
$82 \leq x < 86$	$a$
$86 \leq x < 90$	11
$90 \leq x < 94$	$b$
$94 \leq x < 98$	2

回答下列问题：

(1)、频数分布表中

a =

；

b =

；

(2)、补全频数分布直方图：

(3)、若成绩大于86分为优秀，估计该校七年级300名学生中，达到优秀等级的人数.

查看试题解析

23. 学校为了丰富学生的课余生活，计划购买围棋和中国象棋供棋类兴趣小组活动使用.若购买5副围棋和7副中国象棋需用236元；若购买4副围棋和8副中国象棋需用232元；

(1)、求每副围棋和每副中国象棋各多少元；

(2)、学校决定购买围棋和中国象棋共36副，总费用不超过700元，那么学校最多可以购买多少副围棋？

查看试题解析
24. 我们知道，任意一个大于1的正整数 $n$ 都可以进行这样的分解： $n = x + y$ （ $x$ ， $y$ 均为正整数，且 $x \leq y$ ），在 $n$ 的所有这种分解中，如果 $x$ ， $y$ 两数的乘积最大，我们就称 $x + y$ 是 $n$ 的最佳分解，并规定在最佳分解时： $F (n) = x y$ ，例如6可以分解成 $1 + 5$ ， $2 + 4$ 或 $3 + 3$ ，因为 $1 \times 5 < 2 \times 4 < 3 \times 3$ ，所以 $3 + 3$ 是6的最佳分解，所以 $F (6) = 3 \times 3 = 9$ .

(1)、计算： $F (12)$ ；

(2)、设两位正整数 $t = 10 a + b$ （ $1 \leq a \leq 9$ ， $0 \leq b \leq 9$ ， $a$ ， $b$ 均为整数），数 $t^{'}$ 十位上的数等于数 $t$ 十位上的数与数 $t$ 个位上的数之和，数 $t^{'}$ 个位上的数等于数 $t$ 十位上的数与数 $t$ 个位上的数之差，若 $t^{'} - t = 9$ ，且 $F (t)$ 能被2整除，求两位正整数 $t$ .

查看试题解析
25. 如果一元一次方程的解也是一元一次不等式组的解，则称该一元一次方程为该一元一次不等式组的关联方程.
例如：方程 $2 x - 6 = 0$ 的解为 $x = 3$ ，不等式组 ${\begin{array}{l} x - 2 > 0 ， \\ x < 5 \end{array}$ 的解集为 $2 < x < 5$ ，因为 $2 < 3 < 5$ ，所以，称方程 $2 x - 6 = 0$ 为不等式组 ${\begin{array}{l} x - 2 > 0 ， \\ x < 5 \end{array}$ 的关联方程.

(1)、在方程① $5 x - 2 = 0$ ，② $\frac{3}{4} x + 1 = 0$ ，③ $x - (3 x + 1) = - 5$ 中，不等式组 ${\begin{array}{l} x - \frac{1}{4} < 1 \\ 4 + 2 x > - 7 x + 5 \end{array}$ 的关联方程是；（填序号）

(2)、若不等式组 ${\begin{array}{l} 2 x - 5 > 3 x - 8 \\ - 4 x + 3 < x - 4 \end{array}$ 的一个关联方程的解是整数，则这个关联方程可以是；（写出一个即可）

(3)、若方程 $2 x - 1 = x + 2$ ， $3 + x = 2 (x + \frac{1}{2})$ 都是关于 $x$ 的不等式组 ${\begin{array}{l} x < 2 x - m \\ x - 2 \leq m \end{array}$ 的关联方程，求 $m$ 的取值范围.

查看试题解析
26. 如图1， $A B$ // $C D$ ，点 $E$ 、 $F$ 分别在 $A B$ 、 $C D$ 上，点 $O$ 在直线 $A B$ 、 $C D$ 之间，且 $∠ E O F = 100 °$ .

(1)、求 $∠ B E O + ∠ O F D$ 的值；

(2)、如图2，直线 $M N$ 分别交 $∠ B E O$ 、 $∠ O F C$ 的角平分线于点 $M$ 、 $N$ ，直接写出 $∠ E M N - ∠ F N M$ 的值；

(3)、如图3， $E G$ 在 $∠ A E O$ 内， $∠ A E G = m ∠ O E G$ ； $F H$ 在 $∠ D F O$ 内， $∠ D F H = m ∠ O F H$ ，直线 $M N$ 分别交 $E G$ 、 $F H$ 分别于点 $M$ 、 $N$ ，且 $∠ F M N - ∠ E N M = 50 °$ ，直接写出 $m$ 的值.

查看试题解析