四川省德阳市2020-2021学年七年级下学期数学期末考试试卷

试卷更新日期：2021-08-17 类型：期末考试

进入出卷网下载

一、单选题

1. 在平面直角坐标系中，点 $P (2 ， - 1)$ 在（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
2. 下列各数中：3.141，﹣ $\frac{22}{7}$ ，0，π， $\sqrt[3]{- 27}$ ，0.1010010001……， $\sqrt{9}$ ，无理数有（）

A、2个 B、3个 C、4个 D、5个

查看试题解析
3. 下列不等式变形正确的是（）

A、由a＞b，得a﹣b＞0 B、由a＞b，得ac＞bc C、由a＞b，得 $\frac{a}{c} > \frac{b}{c}$ D、由a＞b，得a²＞ab

查看试题解析
4. 下列调查中，适宜采用全面调查方式的是（）

A、调查一批新型节能灯炮的使用寿命 B、调查长江流域的水污染情况 C、调查广州市初中学生的视力情况 D、为保证“神七”的成功发射，对其零部件进行检查

查看试题解析
5. 如图，如果 $∠ 1 = ∠ 2$ ，那么下面结论正确的是（）

A、 $A D / / B C$ B、 $A B / / C D$ C、 $∠ 3 = ∠ 4$ D、 $∠ A = ∠ C$

查看试题解析
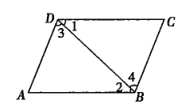6. 与 $\sqrt{7}$ 最接近的整数是（）

A、1 B、2 C、3 D、4

查看试题解析
7. 若点A（a，3），B（2，b）是与y轴平行的直线上不同的两点，且到x轴的距离相等，则点M（a，b）的坐标是（）

A、（2，3） B、（﹣2，3） C、（2，﹣3） D、（﹣2，﹣3）

查看试题解析
8. 我国古代数学著作《孙子算经》中有“鸡兔同笼”问题：含有鸡兔同笼，上有三十五头，下有九十四足，问鸡兔各几何？设鸡有x只，兔有y只，下列方程组正确的是（）

A、 ${\begin{matrix} x + y = 35 \\ 2 x + 4 y = 94 \end{matrix}$ B、 ${\begin{matrix} x + y = 35 \\ 4 x + 2 y = 94 \end{matrix}$ C、 ${\begin{matrix} x + y = 35 \\ 4 x + 4 y = 94 \end{matrix}$ D、 ${\begin{matrix} x + y = 35 \\ x + 4 y = 94 \end{matrix}$

查看试题解析
9. 如图，数轴上A，B两点表示的数分别为﹣1， $\sqrt{5}$ ，且AC＝AB，则点C所表示的数为（）

A、﹣1+ $\sqrt{5}$ B、﹣1﹣ $\sqrt{5}$ C、﹣2﹣ $\sqrt{5}$ D、1+ $\sqrt{5}$

查看试题解析
10. 已知关于x，y的二元一次方程组 ${\begin{array}{l} a x - b y = 4 \\ a x + b y = 2 \end{array}$ 的解是 ${\begin{array}{l} x = 2 \\ y = 1 \end{array}$ ，则 $2 a - 3 b$ 的值是（）

A、6 B、4 C、-4 D、-6

查看试题解析
11. 若关于x的不等式组 ${\begin{array}{l} x - 3 (x - 2) < 4 \\ 3 x - a < 2 x \end{array}$ 无解，则a的取值范围是（）

A、a＜1 B、a≤1 C、a＝1 D、a≥1

查看试题解析
12. 如图，已知A₁（1，0），A₂（1，1），A₃（﹣1，1），A₄（﹣1，﹣1），A₅（2，﹣1）……则点A₂₀₂₁的坐标为（）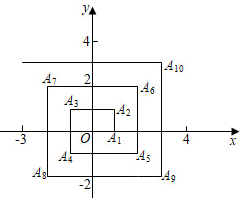

A、（505，﹣504） B、（506，﹣505） C、（505，﹣505） D、（﹣506，506）

查看试题解析

二、填空题

13. 不等式2x﹣1≤3x+2的负整数解的和是 .

查看试题解析
14. 将点A（m+2，m﹣3）向左平移三个单位后刚好落在y轴上，则平移前点A的坐标是 .

查看试题解析
15. 为了解某学校七年级1000名学生的身高，从中抽取200名学生进行测量，在这个问题中，样本是 .

查看试题解析
16. 一条有破损的长方形纸带，按如图折叠，纸带重部分中的∠α的度数为 .

查看试题解析
17. 已知：关于x，y的二元一次方程组 ${\begin{array}{l} 2 x - 3 y = 2 k - 3 \\ x + 5 y = 5 k \end{array}$ 的解满足x﹣8y＞0，则k的取值范围是 .

查看试题解析
18. 已知∠A与∠B一边互相垂直，另一边互相平行，且∠A比∠B大20°，则∠A的度数为 .

查看试题解析

三、解答题

19. 如图，已知∠1＝∠2，AB∥EF，∠3＝130°，求∠4的度数.

查看试题解析
20.

(1)、解方程组： ${\begin{matrix} \frac{1}{2} x - \frac{3}{2} y = - 1 \\ 2 x + y = 3 \end{matrix}$ .

(2)、解不等式组： ${\begin{matrix} - 3 (x - 2) \geq 4 - x \\ \frac{1 + 2 x}{3} > x - 1 \end{matrix}$ .

查看试题解析

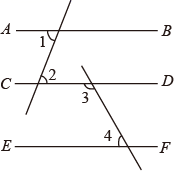21. 某中学开展“创建文明城市”征文比赛活动，赛后随机抽取了部分参赛学生的成绩，按得分划分为A，B，C，D四个等级，并绘制了如下不完整的频数分布表和扇形统计图，根据以上信息，解答以下问题：

等级	成绩（s）	频数（人数）
A	90＜s≤100	6
B	80＜s≤90	x
C	70＜s≤80	24
D	s≤70	9

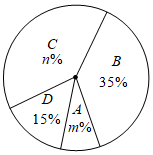(1)、求频数分布表中的x；

(2)、直接写出扇形统计图中m，n的值及C等级对应的扇形的圆心角的度数；

(3)、若该校有1800名学生，请你根据以上数据估计成绩s＞80的学生人数.

查看试题解析

22. 在平面直角坐标系中， $△$ ABC的位置如图所示.

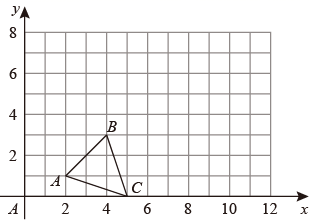(1)、将 $△$ ABC向右平移5个单位长度，再向上平移3个单位长度，得到 $△$ A₁B₁C₁ ，请画出 $△$ A₁B₁C₁ ，并写出 $△$ A₁B₁C₁各顶点的坐标；

(2)、直接写出 $△$ A₁B₁C₁的面积.

查看试题解析
23. 七年级（1）班共有学生48人，班委决定拿出1800元班费举行一次户外拓展活动，计划给每位同学购买一份套餐，其余全部用于发放奖励.现有A、B两种套餐可供选择，已知一份A种套餐比B种套餐多6元，3份A种套餐和2份B种套餐共需153元.经统筹，用于发放奖励的经费不高于300元且A种套餐不多于36份.

(1)、A种套餐和B种套餐的单价分别是多少元？

(2)、请通过计算说明：班委有哪几种购买套餐的方案？如果想有更充足的经费用于发放奖励，应选用哪种方案？

查看试题解析
24. 如图1，在平面直角坐标系中，点A（0，a），B（b，0），C（c，0），且满足 $\sqrt{a - 3}$ +（a+b﹣7）²+|c+a+2|＝0.

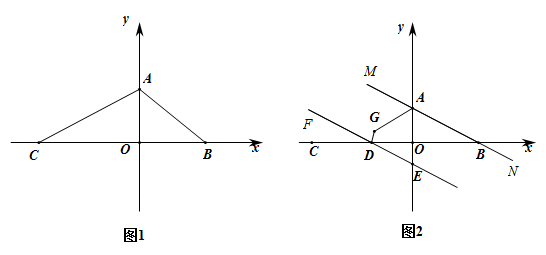(1)、求A、B、C三点的坐标及 $△$ ABC的面积；

(2)、若y轴上有一点H，使得 $△$ ABH的面积等于 $△$ ABC的面积，求点H的坐标；

(3)、如图2，直线MN经过A、B两点，点D是线段CO上一动点（不与端点重合），过点D作EF∥MN交y轴负半轴于点E，∠MAO与∠FDO的角平分线相交于点G，问：∠AGD的度数是否为定值？若是，求出∠AGD的度数，若不是，说明理由.

查看试题解析