陕西省西安市莲湖区2020-2021学年七年级下学期数学期末考试试卷
试卷更新日期：2021-08-17 类型：期末考试
一、单选题
-
1. 下面四个手机应用图标中是轴对称图形的是（ ）A、
B、
C、
D、
2. 熔喷布是口罩最核心的材料，熔喷布主要以聚丙烯为主要原料，其纤维直径最大0.000051米，将0.000051用科学记数法表示为（ ）A、5.1×10﹣6 B、5.1×10﹣5 C、0.51×10﹣7 D、0.51×10﹣73. 下列事件中，属于必然事件的是（ ）A、射击运动员射击一次，命中10环 B、明天会下雨 C、在地球上，抛出去的一块砖头会落下 D、在一个只装有红球的袋中摸出白球4. 如图，将木条a，b与c钉在一起，∠1＝85°，∠2＝45°，要使木条a与b平行，木条a按箭头方向旋转的度数至少是（ ）
A、15° B、25° C、35° D、40°5. 在△ABC中，AB＝10，BC＝1，并且AC的长为偶数，则△ABC的周长为（ ）A、20 B、21 C、22 D、236. 如图，E是△ABC的边AC的中点，过点C作CF//AB，过点E作直线DF交AB于D，交CF于F，若AB＝9，CF＝6.5，则BD的长为（ ）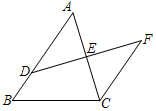
A、1 B、2 C、2.5 D、37. 下列运算中，计算正确的是（ ）A、（﹣2b2）3＝﹣8b6 B、4a4÷2a2＝2a C、2a•4a＝8a D、（a+b）2＝a2+b28. 如图，BP是△ABC中∠ABC的平分线，CP是∠ACB的外角的平分线，若∠ABP＝20°，∠ACP＝60°，则∠A﹣∠P＝（ ）
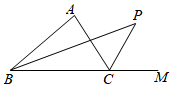A、70° B、60° C、50° D、40°9. 如图，已知∠B＝20°，∠C＝25°，若MP和QN分别垂直平分AB和AC，则∠PAQ等于（ ）
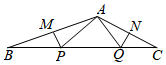A、80° B、90° C、100° D、105°10. 某图书馆的租书收费的相关费用有两种形式，其中一种为月租费，另一种为无月租费.这两种收费方式的y（元）与x（次数）之间的函数关系如图所示.明明根据图象得出下列结论：①l1描述的是无月租费的收费方式.
②l2描述的是有月租费的收费方式.
③当每月租书的次数为30次时.两种收费方式花费一样多.
④琳琳的家人都爱看书，一个月租书次数达到50次，她选择l1较为划算.
其中结论正确的有（ ）
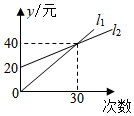A、1个 B、2个 C、3个 D、4个二、填空题
-
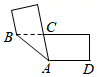
11. 设a，b，c为平面内三条不同的直线，若a⊥c，b⊥c，则a与b的位置关系是.12. 若m2﹣n2＝40，且m﹣n＝5.则m+n＝.13. “彩缕碧筠粽，香梗白玉团”.端午佳节，小琪妈妈准备了豆沙粽2个、红枣粽4个、腊肉粽3个，其中豆沙粽和红枣粽是甜粽.小琪任意选取一个，选到甜粽的概率是 .14. 如图，将一张长方形纸条折叠，若∠CAD＝100°，则∠ABC的度数为 .
三、解答题
-
15. 计算：|﹣ |﹣2﹣1﹣（π﹣4）0 ．16. 先化简，再求值：（m﹣2n）2﹣3n（4n﹣m），其中m＝1，n＝ .17. 已知：△ABC.求作：射线BM，使它平分∠ABC，并在射线BM上找到一点P，使P到B、C两点的距离相等.（保留作图痕迹，不要求写作法）
18. 如图，在△ABC中，∠BAC＝90°，CD//AB交BD于点D，已知∠1＝32°，∠D＝29°，试说明BD平分∠ABC.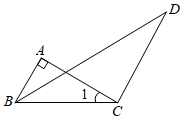
19. 如图，点A，B，C，D在一条直线上，CE与BF交于点O，∠A+∠ABF＝180°，∠E＝∠F，试说明：CE//DF.（将过程补充完整，并写出每一步的推理依据）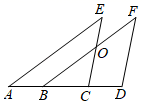
解：因为∠A+∠ABF＝180°（ ），
所以AE//_▲_（ ），
所以∠BOC＝_▲_（ ）.
因为∠E＝∠F（已知），
所以∠F＝_▲_（等量代换）.
所以CE//DF（ ）.
20. 掷一枚质地均匀的骰子，观察向上一面的点数，求下列事件的概率.
(1)、点数为2.(2)、点数为奇数.(3)、点数大于1且小于6.21. 在如图所示的正方形网格中，每个小正方形的边长都是1，△ABC的顶点都在正方形网格的格点（网格线的交点）上.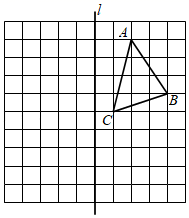
(1)、请在如图所示的网格平面内作出△ABC关于直线l对称的△DEF（点A，B，C的对应点为点D，E，F）.(2)、求出△DEF的面积.22. 如图，在△ABC中，AB＝AC，点D是BC的中点，点E在AB上，BE＝BD，∠BAC＝76°，求∠ADE的大小.
23. 小衡约同学去航天城中湖公园玩，当他骑单车走了一段路到陕铁大厦时，想起要买些饮料和水果，于是又折回到刚经过的某超市，买过饮料和水果后继续去公园.以下是他本次去公园所用的时间与离家距离的关系示意图.根据图中提供的信息回答下列问题：
(1)、小衡家离陕铁大厦的路程是米.(2)、小衡在超市停留了分钟，折回超市的速度为米/分.(3)、在途中哪个时间段小衡骑车速度最快，最快的速度是多少米/分？24. 已知有甲、乙两个长方形，它们的边长如图所示，面积分别为S1 ， S2.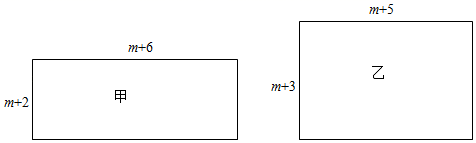
(1)、S1与S2的大小关系为：S1 S2.(2)、若一个正方形的周长与甲的周长相等.①求该正方形的边长（用含m的代数式表示）.
②若该正方形的面积为S3 ， 试探究：S3与S2的差（即S3﹣S2）是否为常数？若为常数，求出这个常数，如果不是，请说明理由.
25. 已知△ABC中，∠ACB＝∠DCE＝α，AC＝BC，DC＝EC，且点A、D、E在同一直线上，AE与BC相交于点F，连接BE.
(1)、如图1，当α＝60°时，求出∠AEB的度数.(2)、如图2，当α＝90°时，若∠CBE＝∠BAE，CF＝2，AB＝8，求△ABF的面积.