湖南省岳阳市2020-2021学年七年级下学期数学期末考试试卷

试卷更新日期：2021-08-17 类型：期末考试

进入出卷网下载

一、单选题

1. 计算（a⁶）²的结果是（）

A、a³ B、a⁴ C、a⁸ D、a¹²

查看试题解析
2. 关于x，y的二元一次方程3x﹣ay＝1有一组解是 ${\begin{matrix} x = 3 \\ y = 2 \end{matrix}$ ，则a的值为（）

A、1 B、2 C、3 D、4

查看试题解析
3. 下列多项式乘法，能用平方差公式计算的是（）

A、 $(- 3 x - 2) (3 x + 2)$ B、 $(- a - b) (- b + a)$ C、 $(- 3 x + 2) (2 - 3 x)$ D、 $(3 x + 2) (2 x - 3)$

查看试题解析
4. 下列交通标志中，是轴对称图形的是 $($ $)$

A、 B、 C、 D、

查看试题解析
5. 疫情无情人有情，爱心捐款传真情，新型冠状病毒感染的肺炎疫情期间，某班学生积极参加献爱心活动，该班50名学生的捐款统计情况如表：

金额/元

5

10

20

50

100

人数

6

17

14

8

5

则他们捐款金额的平均数、中位数、众数分别是（）

A、27.6，10，20 B、27.6，20，10 C、37，10，10 D、37，20，10

查看试题解析
6. 下列各式从左到右因式分解正确的是（）

A、 $2 x - 6 y + 2 = 2 (x - 3 y)$ B、 $x^{2} - 2 x + 1 = x (x - 2) + 1$ C、 $x^{2} - 4 = {(x - 2)}^{2}$ D、 $x^{3} - x = x (x + 1) (x - 1)$

查看试题解析
7. 小亮的妈妈用30元钱买了甲、乙两种水果，甲种水果每千克3元，乙种水果每千克5元，且乙种水果比甲种水果少买了2千克，求小亮妈妈两种水果各买了多少千克？设小亮妈妈买了甲种水果x千克，乙种水果y千克，则可列方程组为（）

A、 ${\begin{array}{l} 3 x + 5 y = 30 \\ x = y - 2 \end{array}$ B、 ${\begin{array}{l} 3 x + 5 y = 30 \\ x = y + 2 \end{array}$ C、 ${\begin{array}{l} 5 x + 3 y = 30 \\ x = y - 2 \end{array}$ D、 ${\begin{array}{l} 5 x + 3 y = 30 \\ x = y + 2 \end{array}$

查看试题解析
8. 如图，有以下四个条件：① $∠ B + ∠ B C D = 180 °$ ，② $∠ 3 = ∠ 4$ ，③ 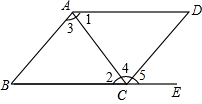$∠ 1 = ∠ 2$ ， ④ $∠ B = ∠ 5$ ，其中不能判定 $A B / / C D$ 的是（）

A、① B、② C、③ D、④

查看试题解析

二、填空题

9. 若 $a^{m} = 3$ ， $a^{n} = 5$ ，则 $a^{m + n} =$ .

查看试题解析
10. 计算 ${(a - 3)}^{2}$ 的结果为

查看试题解析
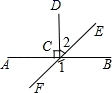
11. 如图，CD⊥AB，垂足为C，∠1=130°，则∠2=度．

查看试题解析
12. 因式分解：2y²﹣18＝．

查看试题解析
13. 已知ab＝2，a﹣b＝3，则a³b﹣2a²b²+ab³＝.

查看试题解析
14. 如图，∠1=∠2，∠A=70°，则∠ADC=度；

查看试题解析
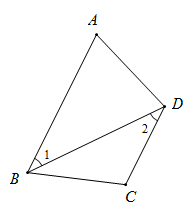15. 一个关于x、y的二元一次方程组的解是 ${\begin{array}{l} x = 2 \\ y = 3 \end{array}$ ，这样的方程组可以是；（只要求写出一个）

查看试题解析
16. 一副直角三角尺叠放如图1所示，现将45°的三角尺ADE固定不动，将含30°的三角尺ABC绕顶点A顺时针转动（旋转角不超过180度），使两块三角尺至少有一组边互相平行.如图2：当∠BAD＝15°时，BC∥DE.则∠BAD（0°＜∠BAD＜180°）其它所有可能符合条件的度数为.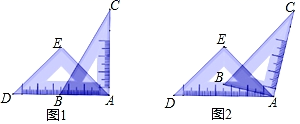

查看试题解析

三、解答题

17. 解方程组：

(1)、 ${\begin{matrix} y = 2 x \\ 3 x + 5 y = 26 \end{matrix}$ ；

(2)、 ${\begin{matrix} 3 x - y = 10 \\ x + y = 2 \end{matrix}$ .

查看试题解析
18. 把下列多项式因式分解：

(1)、x（y﹣3）﹣（2y﹣6）；

(2)、a⁴﹣1.

查看试题解析
19. 求代数式x（2x﹣1）﹣2（x﹣2）（x+1）的值，其中x＝2016.

查看试题解析

20. 为了发展学生的核心素养，培养学生的综合能力，某中学利用“阳光大课间”，组织学生积极参加丰富多彩的课外活动，学校成立了舞蹈队、足球队、篮球队、毽子队、射击队等，其中射击队在某次训练中，甲、乙两名队员各射击10发子弹，成绩记录如表：

射击次序（次）	1	2	3	4	5	6	7	8	9	10
甲的成绩（环）	8	9	7	9	8	6	7	a	10	8
乙的成绩（环）	6	7	9	7	9	10	8	7	7	10

(1)、经计算甲和乙的平均成绩是8（环），请求出表中的a＝；

(2)、甲成绩的中位数是环，乙成绩的众数是环；

(3)、若甲成绩的方差是1.2，请求出乙成绩的方差，判断甲、乙两人谁的成绩更为稳定？

查看试题解析

21. 如图，已知AB∥CD，若∠C=35∘，AB是∠FAD的平分线.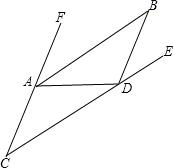

(1)、求∠FAD的度数；

(2)、若∠ADB=110∘，求∠BDE的度数.

查看试题解析
22. 在网格上把△ABC向上平移8小格得到△A₁B₁C₁ ，再作△A₁B₁C₁关于直线MN的轴对称图形得到△A₂B₂C₂_。画出△A₁B₁C₁_、和△A₂B₂C₂.

查看试题解析
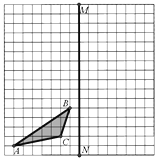23. 安化风景优美，物产丰富，一外地游客到某特产专营店，准备购买黑茶和豆腐乳两种盒装特产．若购买3盒黑茶和2盒豆腐乳共需450元；购买1盒黑茶和3盒豆腐乳共需255元．

(1)、请分别求出每盒黑茶和每盒豆腐乳价格；

(2)、该游客购买了4盒黑茶和2盒豆腐乳，共需多少元？

查看试题解析
24. 如图①，点F，G分别在直线AB，CD上，且AB $//$ CD.

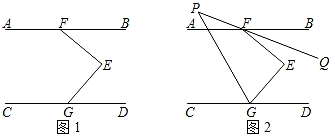(1)、问题发现：若∠BFE＝40°，∠CGE＝130°，则∠GEF的度数为；

(2)、拓展探究：∠GEF，∠BFE，∠CGE之间有怎样的数量关系？并说明理由.

(3)、深入探究：如图②，∠BFE的平分线FQ所在直线与∠CGE的平分线相交于点P，试探究∠GPQ与∠GEF之间的数量关系，请直接写出你的结论.

查看试题解析

金额/元	5	10	20	50	100
人数	6	17	14	8	5