湖南省怀化市部分县区2020-2021学年七年级下学期数学期末考试试卷

试卷更新日期：2021-08-17 类型：期末考试

进入出卷网下载

一、单选题

1. “认识交通标志，遵守交通规则”，下列交通标志中，是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 下列计算正确的是（）

A、 ${(- 2 a)}^{3} = - 6 a^{3}$ B、 $a^{2} \cdot a = a^{2}$ C、 $a^{3} + a^{3} = a^{6}$ D、 ${(- a^{3} b^{2})}^{2} = a^{6} b^{2}$

查看试题解析
3. 一组数据2，4，x，2，4，7的众数是2，则这组数据的平均数、中位数分别为（）

A、3.5，3 B、3，4 C、3，3.5 D、4，3

查看试题解析
4. 下列说法错误的是（）

A、平移不改变图形的形状和大小 B、对顶角相等 C、在同一平面内，垂直于同一条直线的两条直线平行 D、同位角相等

查看试题解析
5. 方程组 ${\begin{array}{l} x + 3 y = 5 \\ x - 6 y = 2 \end{array}$ 的解是（）

A、 ${\begin{array}{l} x = 4 \\ y = \frac{1}{3} \end{array}$ B、 ${\begin{array}{l} x = 2 \\ y = 1 \end{array}$ C、 ${\begin{array}{l} x = 8 \\ y = 1 \end{array}$ D、 ${\begin{array}{l} x = 0 \\ y = 1 \end{array}$

查看试题解析
6. 如图，直线a ，b相交于点O，若∠1等于30°，则∠2等于（）

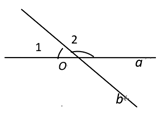A、60° B、70° C、150° D、170°

查看试题解析
7. 同学们把多项式 $2 x^{2} - 4 x y + 2 x$ 提取公因式 $2 x$ 后，则另一个因式应为（）

A、 $x - 2 y$ B、 $x - 2 y + 1$ C、 $x - 4 y + 1$ D、 $x - 2 y - 1$

查看试题解析
8. 如图，直线 $a // b$ ，直线 $l$ 与 $a$ 、 $b$ 分别于点 $A$ 、 $B$ ，过点 $A$ 作 $A C ⊥ b$ 于点 $C$ .若 $∠ 1 = 50 °$ ，则 $∠ 2$ 的度数为（）

A、130° B、50° C、40° D、25°

查看试题解析
9. 如图，在边长为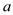的正方形中挖掉一个边长为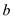的小正方形（，把余下部分剪拼成长方形如右图，通过计算两个图形（阴影部分）的面积，验证了一个等式，这个等式是（）

A、 $(a + 2 b) (a - b) = a^{2} + a b - 2 b^{2}$ B、 ${(a + b)}^{2} = a^{2} + 2 a b + b^{2}$ C、 ${(a - b)}^{2} = a^{2} - 2 a b + b^{2}$ D、 $a^{2} - b^{2} = (a + b) (a - b)$

查看试题解析
10. 为保护生态环境，某县响应国家“退耕还林”号召，将某一部分耕地改为林地，改变后，林地面积和耕地面积共有180平方千米，耕地面积是林地面积的25%，为求改变后林地面积和耕地面积各多少平方千米.设改变后耕地面积x平方千米，林地面积y平方千米，根据题意，列出如下四个方程组，其中正确的是（）

A、 ${\begin{array}{l} x + y = 180 \\ y - x = 25 \frac{0}{0} \end{array}$ B、 ${\begin{array}{l} x + y = 180 \\ x - y = 25 \frac{0}{0} \end{array}$ C、 ${\begin{array}{l} x + y = 180 \\ x = y \cdot 25 \frac{0}{0} \end{array}$ D、 ${\begin{array}{l} x + y = 180 \\ y = x \cdot 25 \frac{0}{0} \end{array}$

查看试题解析

二、填空题

11. 已知 ${\begin{array}{l} x = 1 \\ y = - 1 \end{array}$ 是方程 $3 x - a y = 6$ 的解，则 $a$ =.

查看试题解析
12. 计算 $- 2^{12} \times {(- \frac{1}{2})}^{13}$ 的结果是.

查看试题解析
13. 分解因式：x³－x= ．

查看试题解析
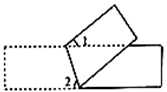
14. 将一个矩形纸片按如图所示折叠，若 $∠ 1 = 40^{\circ}$ ，则 $∠ 2$ 的度数是 $^{\circ}$ .

查看试题解析
15. 如图是一次射击训练中甲、乙两人的10次射击成绩的分布情况，则射击成绩的方差较小的是（填“甲”或“乙”）．

查看试题解析
16. 经计算 $(x - 1) (x + 1) = x^{2} - 1$ ， $(x - 1) (x^{2} + x + 1) = x^{3} - 1$ ，…；以此规律请猜测 $(x - 1) (x^{2021} + x^{2020} + \dots + x + 1) =$ .

查看试题解析

三、解答题

17. 先化简，再求值： $2 x (2 x - y) - {(2 x - y)}^{2}$ ，其中 $x = \frac{1}{2}$ ， $y = - 1$ .

查看试题解析
18. 解二元一次方程组

(1)、 ${\begin{matrix} x + 2 y = 2 \\ x - 2 y = - 2 \end{matrix}$

(2)、 ${\begin{array}{l} 2 (x + y - 1) = 3 (3 - y) - 3 \\ \frac{x}{3} + \frac{y}{2} = 2 \end{array}$

查看试题解析
19. 如图，在正方形网格中，有格点三角形 $A B C$ 和直线 $M N$ .

（ 1 ）画出三角形 $A B C$ 关于直线 $M N$ 对称的三角形 $A_{1} B_{1} C_{1}$ ；

（ 2 ）画出将三角形 $A B C$ 绕点A按逆时针方向旋转90°得到的三角形 $A B_{2} C_{2}$ ；

（ 3 ）画出把三角形 $A B C$ 向右平移一个网格，然后再向上平移四个网格所得三角形 $A_{2} B_{3} C_{3}$ _.（都不要求写作法）

查看试题解析
20. 完成下列两题

(1)、分解因式： $a^{2} (a - b) + 2 a b (b - a) + b^{2} (a - b)$ ；

(2)、已知， $a + b = 4$ ， $a b = - 3$ ，求 ${(a - b)}^{2}$ 的值.

查看试题解析
21. 推理填空：
如图， $∠ 1 + ∠ 2 = 180 °$ ， $∠ A = ∠ C$ ，试说明： $A E // B C$ .

解：因为 $∠ 1 + ∠ 2 = 180 °$ ，

所以 $A B //$ _▲_（               ）

所以 $∠ A$ ＝_▲_（               ）

又因为 $∠ A = ∠ C$ （已知）

所以 $∠ E D C =$ _▲_（等量代换），

所以 $A E // B C$ （     ）

查看试题解析
22. 某中学共有3个一样规模的大餐厅和2个一样规模的小餐厅，经过测试同时开放2个大餐厅和1个小餐厅，可供3000名学生就餐；同时开放1个大餐厅，1个小餐厅，可供1700名学生就餐.

(1)、请问1个大餐厅、1个小餐厅分别可供多少名学生就餐.

(2)、如果3个大餐厅和2个小餐厅全部开放，那么能否供全校4500名学生就餐？请说明理由.

查看试题解析

23. 县射击队要从甲、乙两名运动员中选拔一人参加省里比赛，对他们进行了六次测试，测试成绩如下表（单位：环）：

	第一次	第二次	第三次	第四次	第五次	第六次
甲	10	8	9	8	10	9
乙	10	7	10	10	9	8

(1)、根据表格中数据，分别计算甲、乙的平均测试成绩是多少环？乙运动员测试数据的中位数是多少？

(2)、分别计算甲、乙测试成绩的方差；

(3)、根据（1）、（2）的计算结果，你认为推荐谁参加省里比赛较合适？请说明理由.

查看试题解析

24. 如图， $M N // O P$ ，点A为直线 $M N$ 上一定点，B为直线 $O P$ 上的动点，在直线 $M N$ 与 $O P$ 之间且在线段 $A B$ 的右方作点D，使得 $A D ⊥ B D$ .设 $∠ D A B ＝ α$ （α为锐角）.（提示：三角形三内角和是180°）

(1)、求证 $∠ N A D + ∠ P B D = 90 °$ ；（提示过点D作 $E F // M N$ ）

(2)、当点B在直线 $O P$ 上运动时，试说明 $∠ O B D ﹣ ∠ N A D = 90 °$ ；

(3)、当点B在直线 $O P$ 上运动的过程中，若 $A D$ 平分 $∠ N A B$ ， $A B$ 也恰好平分 $∠ O B D$ ，请求出此时α的值.

查看试题解析