湖北省武汉市新洲区2020-2021学年七年级下学期数学期末考试试卷
试卷更新日期:2021-08-17 类型:期末考试
一、单选题
-
1. 下列所示的图案分别是奔驰、奥迪、长安、三菱汽车的车标,其中看作由“基本图案”经过平移得到的是( )A、
 B、
B、 C、
C、 D、
D、 2. 在平面直角坐标系中,点 在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限3. 在实数 、 、 、 、 、 中,无理数有( )A、2个 B、3个 C、4个 D、5个4. 如图是华联商厦某个月甲、乙、丙三种品牌彩电的销售量统计图,则甲、丙两种品牌彩电该月的销售量之和为( )
2. 在平面直角坐标系中,点 在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限3. 在实数 、 、 、 、 、 中,无理数有( )A、2个 B、3个 C、4个 D、5个4. 如图是华联商厦某个月甲、乙、丙三种品牌彩电的销售量统计图,则甲、丙两种品牌彩电该月的销售量之和为( ) A、50台 B、65台 C、75台 D、95台5. 不等式 的解集在数轴上表示正确的是( )A、
A、50台 B、65台 C、75台 D、95台5. 不等式 的解集在数轴上表示正确的是( )A、 B、
B、 C、
C、 D、
D、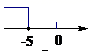 6. 已知点 、点 ,那么线段 的中点的坐标是( )A、 B、 C、 D、7. 若 , , ,则a,b,c的大小关系是( )A、 B、 C、 D、8. 若方程组 的解是负数,则a的取值范围是( )A、-3<a<6 B、a<6 C、a<-3 D、无解9. 如图, , ,点 在 上,点 在 上,设与 相等的角的个数为 (不包括 本身),与 互补的角的个数为 .若 ,则 的值是( )
6. 已知点 、点 ,那么线段 的中点的坐标是( )A、 B、 C、 D、7. 若 , , ,则a,b,c的大小关系是( )A、 B、 C、 D、8. 若方程组 的解是负数,则a的取值范围是( )A、-3<a<6 B、a<6 C、a<-3 D、无解9. 如图, , ,点 在 上,点 在 上,设与 相等的角的个数为 (不包括 本身),与 互补的角的个数为 .若 ,则 的值是( ) A、8 B、9 C、10 D、1110. 如图,直线k∥l, .其中 , ,则 的最大整数值是( )
A、8 B、9 C、10 D、1110. 如图,直线k∥l, .其中 , ,则 的最大整数值是( ) A、108° B、110° C、114° D、115°
A、108° B、110° C、114° D、115°二、填空题
-
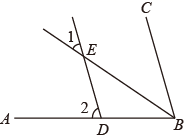
11. 的平方根是 .12. 若点P 在 轴上,则点P的坐标为.13. 如图,已知 , , ,则 的度数是.
 14. 请同学们观察下如表:
14. 请同学们观察下如表:0.04
4
400
40000
0.2
2
20
200
已知 , ,运用你发现的规律求 .
15. 若 ,那么 .16. 下列命题:①对顶角相等;②为了了解某校七年级600名学生的体重情况,从中抽查了50名学生的体重进行统计分析,在这个问题中,总体是指600名学生的体重;③已知正实数 的平方根是 和 ,若 ,则 ;④若不等式 对一切实数 都成立,则 的最大值是5;其中真命题是:.(请填序号)三、解答题
-
17. 解方程:(1)、3(x-2)2=27(2)、2(x-1)3+16=0.18.19. 解不等式组 请按下列步骤完成解答:
(Ⅰ)解不等式①,得_▲_;
(Ⅱ)解不等式②,得_▲_;
(Ⅲ)把不等式①和②的解集在数轴上表示出来;

(Ⅳ)原不等式组的解集为_▲__.
20. 武汉市作为“全国学生近视眼防控工作实验区”,以让学生“不近视、迟近视、慢近视、低近视”,降低学生近视发生率为工作目标.新洲区某校共有1000名学生,为了了解他们的视力情况,随机抽查了部分学生的视力;并将调查的数据整理绘制成直方图和扇形图. (1)、这次共调查了多少名学生?(2)、扇形图中的 , ;(3)、补全频数分布直方图;(4)、求该校学生视力在 的学生共有多少人?21. 如图,每个小正方形的边长为1, 的三个顶点都在格点(小正方形的顶点)上.
(1)、这次共调查了多少名学生?(2)、扇形图中的 , ;(3)、补全频数分布直方图;(4)、求该校学生视力在 的学生共有多少人?21. 如图,每个小正方形的边长为1, 的三个顶点都在格点(小正方形的顶点)上. (1)、已知 ,请写出 、 的坐标: ( , ), ( , );(2)、将 先向右平移6个单位,再向上平移3个单位得 ,请画出平移后的 ,则点 的对应点 的坐标为: (, );(3)、若 的面积为3,则满足条件的格点 有个.22. 某园林公司培育甲种花木2株,乙种花木3株,共需成本1700元;培育甲种花木3株,乙种花木1株,共需成本1500元.(1)、求甲、乙两种花木每株成本分别为多少元?(2)、据市场调研,1株甲种花木售价为760元,1株乙种花木售价为540元.该园林公司决定在成本不超过29000元的前提下培育甲、乙两种花木,若培育乙种花木的株数是甲种花木的3倍还多10株,那么要使总利润不少于21840元,园林公司有哪几种培育方案?23. 如图1,点 在直线 、 之间,且 .
(1)、已知 ,请写出 、 的坐标: ( , ), ( , );(2)、将 先向右平移6个单位,再向上平移3个单位得 ,请画出平移后的 ,则点 的对应点 的坐标为: (, );(3)、若 的面积为3,则满足条件的格点 有个.22. 某园林公司培育甲种花木2株,乙种花木3株,共需成本1700元;培育甲种花木3株,乙种花木1株,共需成本1500元.(1)、求甲、乙两种花木每株成本分别为多少元?(2)、据市场调研,1株甲种花木售价为760元,1株乙种花木售价为540元.该园林公司决定在成本不超过29000元的前提下培育甲、乙两种花木,若培育乙种花木的株数是甲种花木的3倍还多10株,那么要使总利润不少于21840元,园林公司有哪几种培育方案?23. 如图1,点 在直线 、 之间,且 . (1)、求证: ;(2)、若点 是直线 上的一点,且 , 平分 交直线 于点 ,若 ,求 的度数;(3)、如图3,点 是直线 、 外一点,且满足 , , 与 交于点 .已知 ,且 ,则 的度数为(请直接写出答案,用含 的式子表示).24. 如图,平面直角坐标系中, 、 , 轴于点 ,连接 、 .
(1)、求证: ;(2)、若点 是直线 上的一点,且 , 平分 交直线 于点 ,若 ,求 的度数;(3)、如图3,点 是直线 、 外一点,且满足 , , 与 交于点 .已知 ,且 ,则 的度数为(请直接写出答案,用含 的式子表示).24. 如图,平面直角坐标系中, 、 , 轴于点 ,连接 、 . (1)、求 的面积;(2)、若点 是线段 上的一点,且 点的横坐标为 ,求证: ;(3)、线段 以每秒2个单位的速度向右水平移动 秒, 、 的对应点分别 、 ,线段 与 轴交于点 , 的面积记为 , 的面积为 .若 ,请求出 的取值范围.
(1)、求 的面积;(2)、若点 是线段 上的一点,且 点的横坐标为 ,求证: ;(3)、线段 以每秒2个单位的速度向右水平移动 秒, 、 的对应点分别 、 ,线段 与 轴交于点 , 的面积记为 , 的面积为 .若 ,请求出 的取值范围.