湖北省武汉市武昌区2020-2021学年七年级下学期数学期末考试试卷
试卷更新日期:2021-08-17 类型:期末考试
一、单选题
-
1. 在平面直角坐标系中,点 在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限2. 的值是( )A、6 B、±6 C、18 D、±183. 不等式组 的解集在数轴上表示正确的是( )A、
 B、
B、 C、
C、 D、
D、 4. 下列各数中,无理数是( )A、 B、 C、 D、5. 如图,AB∥CD , FE⊥DB于点E , ∠1=48°,则∠2的大小为( )
4. 下列各数中,无理数是( )A、 B、 C、 D、5. 如图,AB∥CD , FE⊥DB于点E , ∠1=48°,则∠2的大小为( ) A、52° B、48° C、42° D、30°6. 是关于 , 的二元一次方程 的一组解,则 的值为( )A、 B、 C、 D、7. 下列调查中,适宜采用全面调查方式的是( )A、一批节能灯管使用寿命的调查 B、对量子科学通信卫星上某种零部件的调查 C、检测武汉市的空气质量 D、对《中国诗词大会》节目收视率的调查8. 如图,数轴上表示实数 的点可能是( )
A、52° B、48° C、42° D、30°6. 是关于 , 的二元一次方程 的一组解,则 的值为( )A、 B、 C、 D、7. 下列调查中,适宜采用全面调查方式的是( )A、一批节能灯管使用寿命的调查 B、对量子科学通信卫星上某种零部件的调查 C、检测武汉市的空气质量 D、对《中国诗词大会》节目收视率的调查8. 如图,数轴上表示实数 的点可能是( ) A、点 B、点 C、点 D、点9. 如图,将一个长方形纸片按图示折叠,若 ,则 的度数是( )
A、点 B、点 C、点 D、点9. 如图,将一个长方形纸片按图示折叠,若 ,则 的度数是( ) A、 B、 C、 D、10. 对 , 定义一种新的运算 ,规定 ,若关于正数 的不等式组 恰好有 个整数解,则 的取值范围是( )A、 B、 C、 D、
A、 B、 C、 D、10. 对 , 定义一种新的运算 ,规定 ,若关于正数 的不等式组 恰好有 个整数解,则 的取值范围是( )A、 B、 C、 D、二、填空题
-
11. 在画频数分布直方图时,一个样本容量为 的样本,最小值为 ,最大值为 .若确定组距为 ,则分成的组数是.12. 如图,直线 AB,CD 相交于点 O,EO⊥AB,垂足为 O,∠BOC:∠COE=13:4,则∠AOC=.
 13. 若关于 , 的二元一次方程组 的解是 ,则关于 , 的二元一次方程组 的解是.14. 甲、乙二人都以不变的速度在环形跑道上跑步,如果同时同地出发,相向而行,每隔 分钟相遇一次;如果同向而行,每隔 分钟相遇一次.已知甲比乙跑得快,则甲每分钟跑圈.15. 若关于 的不等式组 的解集中的任意 的值,都能使不等式 成立,则 的取值范围是.
13. 若关于 , 的二元一次方程组 的解是 ,则关于 , 的二元一次方程组 的解是.14. 甲、乙二人都以不变的速度在环形跑道上跑步,如果同时同地出发,相向而行,每隔 分钟相遇一次;如果同向而行,每隔 分钟相遇一次.已知甲比乙跑得快,则甲每分钟跑圈.15. 若关于 的不等式组 的解集中的任意 的值,都能使不等式 成立,则 的取值范围是.三、解答题
-
16. 解方程组17. 解不等式组18. 填空完成推理过程:
如图, ,求证: .
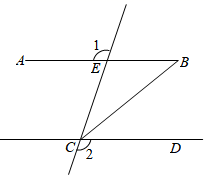
证明: _▲_, (已知)
_▲_.
( )
( ).
19. 如图,三个一样大小的小长方形沿“横-竖-横”排列在一个长为 ,宽为 的大长方形中,求图中一个小长方形的面积. 20. 为积极响应教育部“停课不停学”的号召,某中学组织本校教师开展线上教学,为了解学生线上教学的学习效果,决定随机抽取七年级部分学生进行质量测评,以下是根据测试的数学成绩绘制的统计图表:
20. 为积极响应教育部“停课不停学”的号召,某中学组织本校教师开展线上教学,为了解学生线上教学的学习效果,决定随机抽取七年级部分学生进行质量测评,以下是根据测试的数学成绩绘制的统计图表:成绩分组统计表
成绩 /分
人数(频数)
第 段
第 段
第 段
第 段
第 段

请根据以上信息,解答下列问题:
(1)、此次抽样的样本容量为 , , ;(2)、扇形统计图中,第 段对应的圆心角度数为;(3)、已知该年级有 名学生参加测试,请估计该年级数学成绩为优秀( 分及以上)的人数.21. 某市教育局对某镇实施“教育精准扶贫”,为某镇建了中、小两种图书馆.若建立 个中型图书馆和 个小型图书馆需要 万元,建立 个中型图书馆和 个小型图书馆需要 万元.(1)、建立一个中型图书馆和一个小型图书馆各需要多少万元?(2)、现要建立中型图书馆和小型图书馆共 个,小型图书馆的数量不多于中型图书馆的数量,且总费用不超过 万元,请问有几种方案?哪种方案所需费用最少?
