湖北省武汉市硚口区2020-2021学年七年级下学期数学期末考试试卷

试卷更新日期：2021-08-17 类型：期末考试

进入出卷网下载

一、单选题

1. 实数 $- \sqrt{2}$ 的相反数是（）

A、 $\sqrt{2}$ B、 $- \sqrt{2}$ C、2 D、 $- 2$

查看试题解析
2. 下列调查中，适宜采用全面调查方式的是（）

A、对长江中下游流域水质情况的调查 B、调查某中学七年级（2）班学生视力情况. C、了解一批导弹的杀伤半径 D、了解一批手机电池的使用寿命.

查看试题解析
3. 代数式 $\sqrt{a - 1}$ 在实数范围内有意义，则 $a$ 的取值范围是（）

A、 $a \geq 1$ B、 $a > 1$ C、 $a \geq - 1$ D、 $a > - 1$

查看试题解析
4. 如图，下列条件能判断 $A B // C D$ 的是（）

A、 $∠ 1 = ∠ 2$ B、 $∠ B = ∠ D$ C、 $∠ B A D + ∠ D = 180 °$ D、 $∠ 3 = ∠ 5$

查看试题解析
5. 有大小两种货车，2辆大货车与3辆小货车一次共可运货15.5吨，5辆大货车与6辆小货车一次共可运货35吨，则每辆小货车一次可运货（）

A、2吨 B、2.5吨 C、3吨 D、3.5吨

查看试题解析
6. 如图，直线 $l // m$ ，将含有 $45 °$ 角的三角板 $A B C$ 的直角顶点 $C$ 放在直线 $m$ 上.若 $∠ 1 = 27 °$ ，则 $∠ 2$ 的大小是（）

A、 $27 °$ B、 $28 °$ C、 $16 °$ D、 $18 °$

查看试题解析
7. 某车间每天能生产甲种零件120个或者乙种零件100个.3个甲种零件与2个乙种零件配成一套，要在27天内生产最多的成套产品，问甲、乙两种零件各生产几天？设甲种零件生产 $x$ 天，乙种零件生产 $y$ 天，下列方程组正确的是（）

A、 ${\begin{array}{l} x + y = 27 \\ 120 x = 100 y \end{array}$ B、 ${\begin{array}{l} x + y = 27 \\ 2 \times 120 x = 3 \times 100 y \end{array}$ C、 ${\begin{array}{l} x + y = 27 \\ 3 \times 120 x = 2 \times 100 y \end{array}$ D、 ${\begin{array}{l} x + y = 27 \\ 2 x = 3 y \end{array}$

查看试题解析
8. 关于 $x$ 的不等式组 ${\begin{array}{l} - 5 x + 10 > 0 \\ x + 1 > 2 a \end{array}$ 恰有4个整数解，则实数 $a$ 的取值范围是（）

A、 $- 1 \leq a < 0$ B、 $- 1 < a < - \frac{1}{2}$ C、 $- 1 \leq a \leq - \frac{1}{2}$ D、 $- 1 \leq a < - \frac{1}{2}$

查看试题解析
9. 若实数 $x$ ， $y$ ， $z$ 满足 $2 x - 3 y + z = 7$ ，且 $3 x + y - 2 z = 1$ ，则 $x - 18 y + 11 z - 5$ 的值是（）

A、31 B、27 C、29 D、无法确定

查看试题解析

二、多选题

10. 若 $a > b$ ，则下列不等式不一定成立的是（）

A、 $a - 5 > b - 5$ B、 $- 3 a > - 3 b$ C、 $a c^{2} > b c^{2}$ D、 $\frac{a}{b - a} < \frac{b}{b - a}$

查看试题解析

三、填空题

11. 计算 $\sqrt{{(- 5)}^{2}}$ 的结果是

查看试题解析
12. 某校学生来自甲，乙，丙三个地区，其人数比为 $2 ： 5 ： 8$ ，如图所示的扇形图表示上述分布情况，其中有100人来自甲地区，则该校学生的总数是人.

查看试题解析
13. 将点 $P (- 2 a ， a + 3)$ 向左平移4个单位长度得到的点在第二象限，则 $a$ 的取值范围是.

查看试题解析
14. 关于 $x$ ， $y$ 的方程组 ${\begin{array}{l} 2 x - a y = 1 \\ b x + y = 5 \end{array}$ 的解是 ${\begin{array}{l} x = 2 \\ y = 1 \end{array}$ ，则 $6 a - b$ 的平方根是.

查看试题解析
15. 母亲节来临，小明去花店为妈妈准备节日礼物.已知康乃馨每支2元，百合每支3元.小明将30元钱全部用于购买这两种花（两种花都买），小明的购买方案共有种.

查看试题解析
16. 如图，将长方形纸片 $A B C D$ 沿折痕EF折叠，点 $D$ ， $C$ 的对应点分别为点 $D^{'}$ ， $C^{'}$ ， $C^{'} D^{'}$ 交 $B C$ 于点 $G$ ，再把三角形 $G C^{'} F$ 沿 $G F$ 折叠，点 $C^{'}$ 的对应点为点 $H$ ，若 $∠ D^{'} G H = 104 °$ ，则 $∠ D E D^{'}$ 的大小是.

查看试题解析

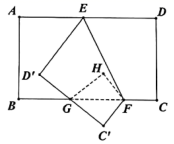
四、解答题

17. 解下列方程组：

(1)、 ${\begin{array}{l} 3 x - y = 11 ， ① \\ 4 x + 3 y = - 7. ② \end{array}$

(2)、 ${\begin{array}{l} a - b + c = 0 ， ① \\ 4 a + 2 b + c = 3 ， ② \\ 25 a + 5 b + c = 60. ③ \end{array}$

查看试题解析
18. 解不等式组 ${\begin{array}{l} x + 4 \geq 3 (x + 2) ， ① \\ 3 x - 3 < 2 x . ② \end{array}$ 请按下列步骤完成解答：
（Ⅰ）解不等式①，得_▲_；

（Ⅱ）解不等式②，得_▲_；

（Ⅲ）把不等式①和②的解集在数轴上表示出来：

（Ⅳ）原不等式组的解集为_▲_.

查看试题解析
19. 某校为了解本校七年级学生参加党史知识比赛成绩情况（满分100分），随机抽取了部分学生的党史知识比赛成绩，并将他们的成绩按四个等级：A（100~90分），B（89~80分），C（79~60分），D（59~0分）进行整理，绘制如下两幅不完整的统计图.根据图中提供的信息，解答下列问题：

(1)、这次随机抽取的学生共有人，在扇形统计图中A等级所对应的扇形国心角的大小为；

(2)、请补全条形统计图；

(3)、该校七年级共有学生900人，若分数为80分（含80分）以上为优秀，估计七年级参加党史知识比赛成绩为优秀的学生人数.

查看试题解析
20. 如图、点 $C$ 、 $F$ 均在直线 $G$ 上，点 $E$ 在直线 $A D$ 上，连接 $A B$ ， $C D$ ， $A F$ 平分 $∠ B A D$ 交 $C D$ 于 $M$ ，连接 $E F$ ， $∠ D A M = ∠ D M A$ ， $∠ B = ∠ D$ .求证： $∠ E = ∠ E F B$ .

查看试题解析
21. 如图，三角形 $A B C$ 的顶点坐标为 $A (- 1 ， 4)$ ， $B (- 3 ， 1)$ ， $C (0 ， 2)$ ， $A B$ 交网格线于点 $K$ ，将三角形 $A B C$ 平移至三角形 $D E F$ ，点 $A$ 对应点 $D$ （1，3），点 $B$ 对应点 $E$ ，点 $C$ 对应点 $F$ .

（ 1 ）画三角形 $D E F$ ，写出点 $E$ 坐标；

（ 2 ）直接写出三角形 $D E F$ 的面积；

（ 3 ）用无刻度的直尺画出点 $K$ 关于 $y$ 轴的对称点 $L$ （用虚线保留画图痕迹）；

（ 4 ）直接写出直线 $B E$ 与 $y$ 轴的交点坐标.

查看试题解析
22. 某商场若购进2部甲型号手机和3部乙型号手机，共需7400元；若购进3部甲型号手机和5部乙型号手机，共需11700元.

(1)、求甲、乙型号手机每部的进价；

(2)、商场计划用不少于44400元且不多于50000元的资金购进这两种型号手机共30台.
①求有多少种进货方案；

②若每部甲，乙型号手机的售价分别为2500元，1950元，为了促销.商场决定每售出一部乙型号手机，返还顾客现金 $a$ 元（ $a \geq 150$ ，且 $a$ 为50的整数倍），要使每一种进货方案（全都售完）获利均不低于15300元，求 $a$ 的值.

查看试题解析
23. 已知直线 $E F$ 分别交直线 $A B$ 、 $C D$ 于点 $G$ 、 $H$ ， $∠ 1 + ∠ 2 = 180 °$ .

(1)、如图1，求证： $A B // C D$ ；

(2)、如图2， $M$ 、 $N$ 分别为直线 $A B$ 、 $C D$ 上的点， $P$ 、 $Q$ 为直线 $A B$ 、 $C D$ 之间不同的两点， $∠ P M Q = 2 ∠ B M Q$ ， $∠ P N Q = 2 ∠ D N Q$ ， $∠ M Q N = 30 °$ .
①求证： $P M ⊥ P N$ ；

②如图3， $∠ E G B$ 的平分线 $G L$ 与 $∠ M P N$ 的邻补角 $∠ M P T$ 的平分线 $P L$ 交于点 $L$ ， $∠ P N H$ 的平分线 $N K$ 交 $E F$ 于点 $K$ .若 $∠ E K N + ∠ G L P = 170 °$ ，∠LPT=40°，直接写出 $∠ P N H - ∠ E H D$ 的大小.

查看试题解析
24. 如图1，在平面直角坐标系中，三角形 $A B C$ 的顶点坐标分别为 $A (a ， 5)$ ， $B (4 ， 2)$ ， $C (c ， 5)$ ，且 $\sqrt{2 a + c - 1} + | 3 a - c - 9 | = 0$ .

(1)、直接写出 $a =$ ， $c =$ ；三角形 $A B C$ 的面积为；

(2)、如图2，将线段 $A B$ 平移至对应线段 $C D$ ， $y$ 轴上点 $E (0 ， - 1)$ ，满足 $B E = 5$ ， $F$ 为线段 $D E$ 延长线上一点， $F M ⊥$ 直线 $A C$ 于 $M$ ， $F N ⊥$ 直线 $B E$ 于 $N$ ，试求 $F M - F N$ 的值；

(3)、如图3，点 $P (n ， 0)$ 在 $x$ 轴上，记三角形 $A B P$ 的面积为 $S$ ，若 $\frac{2}{3} \leq S < 14$ ，直接写出 $n$ 的取值范围.

查看试题解析