湖北省武汉市江岸区2020-2021学年七年级下学期数学期末考试试卷
试卷更新日期:2021-08-17 类型:期末考试
一、单选题
-
1. 计算 的结果为( )A、 B、3 C、 D、92. 在平面直角坐标系中,点P(﹣3,-1)在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限3. 不等式组解集为 ,下列在数轴上表示正确的是( )A、
 B、
B、 C、
C、 D、
D、 4. 下列采用的调查方式中,合适的是( )A、调查某批次汽车的抗撞击能力,采用全面调查的方式 B、为了解东湖的水质情况,采用抽样调查的方式 C、某小型企业给在职员工做工作服前进行尺寸大小的调查,采用抽样调查的方式 D、某市教育部门为了解该市中小学生的视力情况,采用全面调查的方式5. 如图,以下说法错误的是( )
4. 下列采用的调查方式中,合适的是( )A、调查某批次汽车的抗撞击能力,采用全面调查的方式 B、为了解东湖的水质情况,采用抽样调查的方式 C、某小型企业给在职员工做工作服前进行尺寸大小的调查,采用抽样调查的方式 D、某市教育部门为了解该市中小学生的视力情况,采用全面调查的方式5. 如图,以下说法错误的是( ) A、若 ,则 B、若 ,则 C、若 ,则 D、若 ,则6. 若 ,下列不等式不一定成立的是( )A、 B、 C、 D、7. 《九章算术》中的方程问题:“五只雀、六只燕,共重 斤(古代 斤= 两),雀重燕轻,互换其中一只,恰好一样重,问:每只雀、燕的重量各为多少?”设每只雀、燕的重量各为 两、 两,下列方程组正确的为( )A、 B、 C、 D、8. 如图所示,在平面直角坐标系中,半径均为1个单位长度的半圆 , , ……,组成一条平滑的曲线,点 从原点 出发,沿这条曲线向右运动,每秒运动的路程为 个单位长度,则第2021秒时,点 的坐标是( )
A、若 ,则 B、若 ,则 C、若 ,则 D、若 ,则6. 若 ,下列不等式不一定成立的是( )A、 B、 C、 D、7. 《九章算术》中的方程问题:“五只雀、六只燕,共重 斤(古代 斤= 两),雀重燕轻,互换其中一只,恰好一样重,问:每只雀、燕的重量各为多少?”设每只雀、燕的重量各为 两、 两,下列方程组正确的为( )A、 B、 C、 D、8. 如图所示,在平面直角坐标系中,半径均为1个单位长度的半圆 , , ……,组成一条平滑的曲线,点 从原点 出发,沿这条曲线向右运动,每秒运动的路程为 个单位长度,则第2021秒时,点 的坐标是( ) A、 B、 C、 D、9. 下列命题:①方程 有无数组整数解﹔②垂直于同一直线的两条直线互相平行﹔③若 是关于 的一元一次不等式,则 ;④若 ,则点 在第二、四象限.其中是真命题的个数是( )A、1个 B、2个 C、3个 D、4个10. 已知关于 的不等式组 有且只有两个整数解,则 的取值范围是( )A、 B、 C、 D、
A、 B、 C、 D、9. 下列命题:①方程 有无数组整数解﹔②垂直于同一直线的两条直线互相平行﹔③若 是关于 的一元一次不等式,则 ;④若 ,则点 在第二、四象限.其中是真命题的个数是( )A、1个 B、2个 C、3个 D、4个10. 已知关于 的不等式组 有且只有两个整数解,则 的取值范围是( )A、 B、 C、 D、二、填空题
-
11. 要使 有意义,则x的取值范围是 .12. 若 是关于 , 的二元一次方程 的解,则 的值为.13. 如图,已知点 为 内一点, , , 交 于点 ,若 ,则 的度数为.
 14. 如图第一象限内有两点 , ,将线段 平移,使点 、 分别落在两条坐标轴上,则点 平移后的对应点的坐标是.
14. 如图第一象限内有两点 , ,将线段 平移,使点 、 分别落在两条坐标轴上,则点 平移后的对应点的坐标是. 15. 如图,两个形状、大小完全相同的大长方形内放入五个如图③的小长方形后分别得到图①、图②,已知大长方形的长为 ,则图①中阴影部分的周长与图②中阴影部分的周长的差是.(用含 的式子表示)
15. 如图,两个形状、大小完全相同的大长方形内放入五个如图③的小长方形后分别得到图①、图②,已知大长方形的长为 ,则图①中阴影部分的周长与图②中阴影部分的周长的差是.(用含 的式子表示) 16. 现有一元、五元、十元纸币各12张,从中抽取21张,共值100元,则十元纸币取张.
16. 现有一元、五元、十元纸币各12张,从中抽取21张,共值100元,则十元纸币取张.三、解答题
-
17. 解方程组:18. 解不等式组:19. 某校组织全体学生开展汉字听写大赛,从中抽取部分学生成绩(得分为正整数,满分为100分)进行统计,绘制了两幅不完整的统计图,直方图从左至右分别对应A、B、C、D、E组,其中C组图象缺失.已知A组的频数比B组小48.
请你根据图中提供的信息解答下列问题:
 (1)、求频数分布直方图中的a、b的值;(2)、求扇形图中D部分所对的圆心角的度数,并补全频数分布直方图;(3)、若80分以上为优秀,全校共有1000名学生,估计成绩优秀的学生有多少名?20. 如图, 于 , 于 ,
(1)、求频数分布直方图中的a、b的值;(2)、求扇形图中D部分所对的圆心角的度数,并补全频数分布直方图;(3)、若80分以上为优秀,全校共有1000名学生,估计成绩优秀的学生有多少名?20. 如图, 于 , 于 , (1)、求证: ;(2)、若 , 平分 ,求证: 平分 .21. 如图,在平面直角坐标系中,所给的正方形网格的每个小正方形边长均为1个单位,每个小正方形的顶点称为格点, 的三个顶点均在格点上,位置如图所示,其中 .现将 沿 的方向平移,使得点 平移至图中的 的位置.
(1)、求证: ;(2)、若 , 平分 ,求证: 平分 .21. 如图,在平面直角坐标系中,所给的正方形网格的每个小正方形边长均为1个单位,每个小正方形的顶点称为格点, 的三个顶点均在格点上,位置如图所示,其中 .现将 沿 的方向平移,使得点 平移至图中的 的位置. (1)、在图中画出 ,写出点 的坐标为_▲_,点 的坐标为_▲_;(2)、线段 沿 的方向平移到 的过程中扫过的面积是;(直接填写结果)(3)、将直线 以每秒1个单位长度的速度向右平移,平移秒时该直线恰好经点 .(直接填写结果)22. 某网上商城购进甲,乙两种商品共100件,若甲种商品进价为80元每件,乙种商品进价为50元每件,已知在销售过程中,2件甲种商品比3件乙种商品的售价多30元,3件甲种商品和5件乙种商品的售价共710元.(1)、求甲、乙两种商品每件的售价分别是多少元?(2)、若商城计划甲、乙两种商品的进货总投人不超过6050元,销售完后总利润不低于2640元,共有多少种进货方案?(3)、商城为尽快回笼资金,采取优惠活动,甲种商品售价下调 元( ),乙种商品售价保持原价.若该商城保持甲、乙两种商品进价不变,并且该商城无论如何进货,这100件商品销售总利润不变,求 的值.23. 已知直线 与直线 、 分别交于 、 两点, 和 的角平分线交于点 ,且 .(1)、求证: ;
(1)、在图中画出 ,写出点 的坐标为_▲_,点 的坐标为_▲_;(2)、线段 沿 的方向平移到 的过程中扫过的面积是;(直接填写结果)(3)、将直线 以每秒1个单位长度的速度向右平移,平移秒时该直线恰好经点 .(直接填写结果)22. 某网上商城购进甲,乙两种商品共100件,若甲种商品进价为80元每件,乙种商品进价为50元每件,已知在销售过程中,2件甲种商品比3件乙种商品的售价多30元,3件甲种商品和5件乙种商品的售价共710元.(1)、求甲、乙两种商品每件的售价分别是多少元?(2)、若商城计划甲、乙两种商品的进货总投人不超过6050元,销售完后总利润不低于2640元,共有多少种进货方案?(3)、商城为尽快回笼资金,采取优惠活动,甲种商品售价下调 元( ),乙种商品售价保持原价.若该商城保持甲、乙两种商品进价不变,并且该商城无论如何进货,这100件商品销售总利润不变,求 的值.23. 已知直线 与直线 、 分别交于 、 两点, 和 的角平分线交于点 ,且 .(1)、求证: ;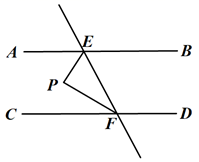 (2)、如图, 和 的角平分线交于点 ,求 的度数;
(2)、如图, 和 的角平分线交于点 ,求 的度数; (3)、如图,若 ,延长线段 得射线 ,延长线段 得射线 ,射线 绕点 以每秒15°的速度逆时针旋转360°后停止,射线 绕点 以每秒3°的速度顺时针旋转180°以后停止.设它们同时旋转 秒,问 为多少时,射线 ,直接写出 的值 秒.
(3)、如图,若 ,延长线段 得射线 ,延长线段 得射线 ,射线 绕点 以每秒15°的速度逆时针旋转360°后停止,射线 绕点 以每秒3°的速度顺时针旋转180°以后停止.设它们同时旋转 秒,问 为多少时,射线 ,直接写出 的值 秒. 24. 已知在平面直角坐标系中, 为坐标原点,点 的坐标为 ,点 的坐标为 ,
24. 已知在平面直角坐标系中, 为坐标原点,点 的坐标为 ,点 的坐标为 , (1)、若 、 满足 ,求点 、点 的坐标;(2)、若点 为直线 上一动点(点 异于点 、 ),在(1)的条件下, ,求 点横坐标 的取值范围;(3)、若 、 、 符合 ,且满足 , , 是代数式 的最大值, 点的坐标是 , 是第一象限内线段 上方的动点,连 交直线 于 点,当 时,且代数式 取最大值时,求 .
(1)、若 、 满足 ,求点 、点 的坐标;(2)、若点 为直线 上一动点(点 异于点 、 ),在(1)的条件下, ,求 点横坐标 的取值范围;(3)、若 、 、 符合 ,且满足 , , 是代数式 的最大值, 点的坐标是 , 是第一象限内线段 上方的动点,连 交直线 于 点,当 时,且代数式 取最大值时,求 .