湖北省潜江市2020-2021学年七年级下学期数学期末考试试卷

试卷更新日期：2021-08-17 类型：期末考试

进入出卷网下载

一、单选题

1. 下列实数中是无理数的是（）

A、 $3.14$ B、 $\sqrt{4}$ C、 $\sqrt{2}$ D、 $\frac{1}{7}$

查看试题解析
2. 下列调查中，适合采用全面调查方式的是（）

A、了解我市的空气质量 B、了解我市居民家庭的收入情况 C、了解某班学生的视力情况 D、了解春节联欢晚会的收视率

查看试题解析
3. 如图，把一个长方形纸片沿EF折叠后，点D、C分别落在D′、C′的位置，若∠EFB=65°，则∠AED′等于（）

A、50° B、55° C、60° D、65°

查看试题解析
4. 已知点P $(a ， b)$ 在第四象限，则点Q $(a b ， b - a)$ 在（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
5. 下列说法正确的是（）

A、1的立方根是±1 B、-1的平方根是-1 C、4的算术平方根是±2 D、5是 25的算术平方根

查看试题解析
6. 为了记录一个病人的体温变化情况，应选择的统计图是（）

A、条形统计图 B、扇形统计图 C、折线统计图 D、频数分布直方图

查看试题解析
7. 雅安地震后，灾区急需帐篷。某企业急灾区之所急，准备捐助甲、乙两种型号的帐篷共1500顶，其中甲种帐篷每顶安置6人，乙种帐篷每顶安置4人，共安置8000人．设该企业捐助甲种帐篷x顶、乙种帐篷y顶，那么下面列出的方程组中正确的是( )

A、 $\{\begin{matrix} x + 4 y = 1500 \\ 4 x + y = 8000 \end{matrix}$ B、 $\{\begin{matrix} x + 4 y = 1500 \\ 6 x + y = 8000 \end{matrix}$ C、 $\{\begin{matrix} x + y = 1500 \\ 4 x + 6 y = 8000 \end{matrix}$ D、 $\{\begin{matrix} x + y = 1500 \\ 6 x + 4 y = 8000 \end{matrix}$

查看试题解析
8. 不等式组 ${\begin{cases} \end{cases} \begin{array}{l} 2x+3>5 \\ 3x - 2<4 \end{array}$ 的解等于（）.

A、1<x<2 B、x>1 C、x<2 D、x<1或x>2

查看试题解析
9. 下列命题：①对顶角相等；②内错角相等；③平行于同一条直线的两条直线互相平行；④如果一个角的两边分别平行于另一个角的两边，那么这两个角相等.其中真命题是（）

A、①③ B、①④ C、①③④ D、①②③④

查看试题解析
10. 小明带着20元钱到超市购买笔和练习本，每支笔3元，每个练习本2元，若两种物品都要购买且把20元钱花完，则共有几种不同的购买方案（）

A、2种 B、3种 C、4种 D、5种

查看试题解析

二、填空题

11. 将命题“同角的补角相等”改写成“如果……那么……”的形式为

查看试题解析
12. 如图，直线AB，CD交于点O， $∠ B O C = 70 °$ ，现作射线OE⊥CD，则∠AOE的大小为.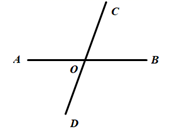

查看试题解析
13. 已知 ${\begin{array}{l} x = 2 \\ y = 1 \end{array}$ 是方程 $3 x - 4 y - 2 a = 0$ 的解，则 $a$ =.

查看试题解析
14. 在平面直角坐标系中，已知线段AB∥x轴，端点A的坐标是（﹣1，4）且AB=4，则端点B的坐标是．

查看试题解析
15. 某种服装的进价为240元，出售时标价360元，由于换季，商店准备打折销售，但要保证利润不低于20%，则最多能打折.

查看试题解析
16. 如图，正方形ABCD的各边分别平行于x 轴或y 轴，且CD边的中点坐标为（2，0），AD 边的中点坐标为（0，2）.点M，N分别从点（2，0）同时出发，沿正方形ABCD的边作环绕运动.点M按逆时针方向以1个单位/秒的速度匀速运动，点N按顺时针方向以3个单位/秒的速度匀速运动，则M，N两点出发后的第2020次相遇地点的坐标是.

查看试题解析

三、解答题

17.

(1)、计算： $\sqrt[3]{8} + | \sqrt{2} - 3 | - \sqrt{25} + \sqrt{2}$ ；

(2)、已知 ${(1 - x)}^{3} = - 8$ ，求 $x$ 的值.

(3)、已知实数 $x ， y$ 满足： ${\begin{array}{l} 4 x - 3 y = 11 \\ 2 x - y = 13 \end{array}$ ，求 $x - y$ 的值.

查看试题解析
18. 解不等式组： ${\begin{array}{l} 3 (x + 2) > x + 8 \\ \frac{x}{4} \geq \frac{x - 1}{3} \end{array}$ 并把它的解集在数轴上表示出来.

查看试题解析
19. 如图，在正方形网格中，每个小正方形的边长为1，格点三角形（顶点是网格线的交点的三角形）ABC的顶点A，C的坐标分别为（-4，5），（-1，3）.

(1)、请在如图所示的网格平面内作出平面直角坐标系；

(2)、请把△ABC先向右平移5个单位，再向下平移3个单位得到△A′B′C′，在图中画出△A′B′C′，并写出点B的对应点B′的坐标；

(3)、求△ABC的面积.

查看试题解析
20. 去年疫情期间，很多学校开展了线上授课相关工作.为了更好地提高学生线上授课的效果，某中学进行了线上授课问卷调查.其中一项调查是：你认为影响师生互动的最主要因素是：A.教师的授课理念；B.网络设备等硬件问题；C.科目特点；D.学生的配合情况.针对这个调查，问卷时要求每位同学必须且只能选择其中一项.现随机抽取了若干名学生的调查问卷，将所得数据进行整理，制成如下条形统计图和扇形统计图.

根据以上信息解答下列问题：

(1)、本次抽样调查了名学生；

(2)、补全条形统计图，扇形统计图中扇形“方式A”的圆心角为度；

(3)、若该校共有2000名学生，根据调查结果，请你估计认为影响师生互动的最主要因素是“C. 科目特点”的学生共有多少人？

查看试题解析
21. 推理填空.
如图，AB∥CD，EF分别交AB，CD于G，N；GH，NM分别平分∠AGN，∠GND.

求证：GH∥NM.

证明：∵AB∥CD（         ）

∴∠AGN=∠_▲_（                ）

∵GH，NM分别平分∠AGN，∠GND

∴∠HGN= $\frac{1}{2}$ ∠AGN，

∠MNG= $\frac{1}{2}$ ∠GND（                  ）

∴∠_▲_=∠MNG（                    ）

∴GH∥NM（                             ）

查看试题解析
22. 2010年春季我国西南大旱，导致大量农田减产，如图所示是一对农民父子的对话内容，请根据对话内容分别求出该农户今年两块农田的花生产量分别是多少千克?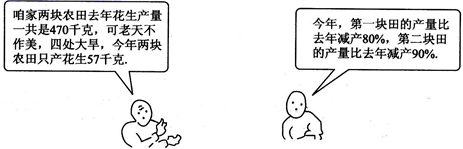

查看试题解析
23. 三角形ABC中，DE∥BC分别交AB，AC于点D，E，点F在直线BC上，作直线EF，过点D作直线DG∥AC交直线EF于点G.

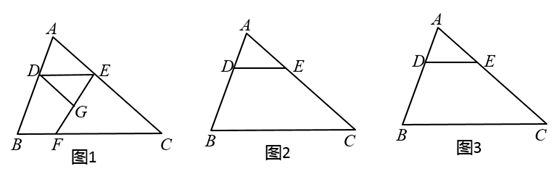(1)、如图1，若点F在线段BC上，求证：∠EDG=∠C；

(2)、若点F在线段BC的反向延长线上，请在图2中作出相应的图形，并探究∠DGF与∠CEF的数量关系；

(3)、若点F在线段BC的延长线上，请在图3中作出相应的图形，此时（2）中的结论是否仍然成立，并说明理由.

查看试题解析

24. 甲、乙两商场以同样价格出售同样的商品，并且又各自推出不同的优惠方案：在甲商场累计购物超过200元后，超出200元的部分按80%收费；在乙商场累计购物超过100元后，超出100元的部分按90%收费.设小华在同一商场累计购物x元，其中x＞200.

小华累计购物（单位：元）	250	390	…	x
甲商场实际收费（单位：元）	240	a	…	m
乙商场实际收费（单位：元）	235	b	…	n

(1)、根据题意及表中提供的信息填空：a= ， b=；m= ， n=；

(2)、当x取何值时，甲、乙两商场的实际收费相同？

(3)、当小华在同一商场累计购物超过200元时，哪家商场的实际收费少，为什么？

查看试题解析