湖北省鄂州市2020-2021学年七年级下学期数学期末考试试卷
试卷更新日期:2021-08-17 类型:期末考试
一、单选题
-
1. 下列实数中,是无理数的是( )A、 B、 C、 D、2. 在平面直角坐标系中,点P(2, 1)所在的象限是( )A、第一象限 B、第二象限 C、第三象限 D、第四象限3. 如图,直线 与 相交于点 ,若 ,则 等于( )
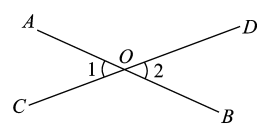 A、 B、 C、 D、4. 植物园中有红豆杉、马尾松、长白松、银杏四种国家级保护植物,为了解本班同学喜欢哪种植物的人最多,需要进行调查,则调查的对象是( ).A、本班的每一名同学 B、红豆杉、马尾松、长白松、银杏 C、同学们的选票 D、记录下来的数据5. 已知实数 , 满足 ,则下列结论中,不正确的是( )A、 B、 C、 D、6. 小明将本班全体同学某次数学测试成绩制成了频数分布直方图,直方图中从左到右各小长方形的高之比为 ,即表示第一组到第四组这四组人数之比为 ,且第四组的频数是 ,则小明班的学生人数是( )A、 B、 C、 D、7. 如图,下面推理过程正确的是( )
A、 B、 C、 D、4. 植物园中有红豆杉、马尾松、长白松、银杏四种国家级保护植物,为了解本班同学喜欢哪种植物的人最多,需要进行调查,则调查的对象是( ).A、本班的每一名同学 B、红豆杉、马尾松、长白松、银杏 C、同学们的选票 D、记录下来的数据5. 已知实数 , 满足 ,则下列结论中,不正确的是( )A、 B、 C、 D、6. 小明将本班全体同学某次数学测试成绩制成了频数分布直方图,直方图中从左到右各小长方形的高之比为 ,即表示第一组到第四组这四组人数之比为 ,且第四组的频数是 ,则小明班的学生人数是( )A、 B、 C、 D、7. 如图,下面推理过程正确的是( ) A、因为 ,所以 B、因为 ,所以 C、因为 ,所以 D、因为 ,所以8. 小轩解方程组 的解为 ,由于不小心滴上了两滴墨水,刚好遮住了两个数●和★,则两个数●与★的值分别为( )A、 B、 C、 D、9. 象棋在中国有着三千多年的历史,由于用具简单,趣味性强,成为流行极为广泛的益智游戏.如图,是一局象棋残局,帅位于 ,相位于点 ,则炮位于( )
A、因为 ,所以 B、因为 ,所以 C、因为 ,所以 D、因为 ,所以8. 小轩解方程组 的解为 ,由于不小心滴上了两滴墨水,刚好遮住了两个数●和★,则两个数●与★的值分别为( )A、 B、 C、 D、9. 象棋在中国有着三千多年的历史,由于用具简单,趣味性强,成为流行极为广泛的益智游戏.如图,是一局象棋残局,帅位于 ,相位于点 ,则炮位于( )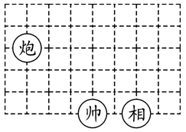 A、 B、 C、 D、10. 如图所示的是一个运算程序,例如:根据所给的运算程序可知:当 时, ,则输出的值为 ;当 时, ,再把 代入,得 ,则输出的值为 .若数 需要经过三次运算才能输出结果,则 的取值范围是( )
A、 B、 C、 D、10. 如图所示的是一个运算程序,例如:根据所给的运算程序可知:当 时, ,则输出的值为 ;当 时, ,再把 代入,得 ,则输出的值为 .若数 需要经过三次运算才能输出结果,则 的取值范围是( ) A、 B、 C、 D、 或
A、 B、 C、 D、 或二、填空题
-
11. 4的算术平方根是 .12. 我国古代数学名著《数学九章》有“米谷粒分”题:粮仓开仓收粮,有人送来米 石,验得米内夹谷,抽样取米一把,数得 粒内夹谷 粒,则这批米内夹谷约为石.13. 已知点 在第二象限,则 的范围是.14. 如图,把一个直角三角尺的直角顶点放在直尺的一边上,若 ,则 .
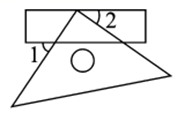 15. 已知 是二元一次方程组 的解,则 的立方根 .16. 定义:对于实数 ,符号 表示不大于 的最大整数.例如: , , .如果 ,那么 的取值范围是.17. 如图,两个相同直角三角形重叠在一起,将其中一个沿着 的方向平移到 的位置, , , ,阴影部分的面积为 ,则平移距离 长 .
15. 已知 是二元一次方程组 的解,则 的立方根 .16. 定义:对于实数 ,符号 表示不大于 的最大整数.例如: , , .如果 ,那么 的取值范围是.17. 如图,两个相同直角三角形重叠在一起,将其中一个沿着 的方向平移到 的位置, , , ,阴影部分的面积为 ,则平移距离 长 .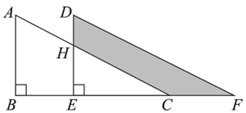 18. 在平面直角坐标系中,对于点 ,如果点 的纵坐标满足 ,那么称点 为点 的“关联点”.例如点 的“关联点”的坐标为点 ;如果点 的关联点 的坐标为 ,则此时 .
18. 在平面直角坐标系中,对于点 ,如果点 的纵坐标满足 ,那么称点 为点 的“关联点”.例如点 的“关联点”的坐标为点 ;如果点 的关联点 的坐标为 ,则此时 .三、解答题
-
19. 计算(1)、 ;(2)、 .20. 解下列不等式(组)(1)、 ;(2)、 .21. 已知:如图, , ;
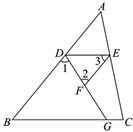 (1)、求证: ;(2)、求证: ;(3)、若 , .求 的度数.22. 如图,在平面直角坐标系中,网格中的每一个小方格都是边长为 个单位的小正方形,小正方形的每一个顶点称之为格点, 三个顶点均在格点上.
(1)、求证: ;(2)、求证: ;(3)、若 , .求 的度数.22. 如图,在平面直角坐标系中,网格中的每一个小方格都是边长为 个单位的小正方形,小正方形的每一个顶点称之为格点, 三个顶点均在格点上.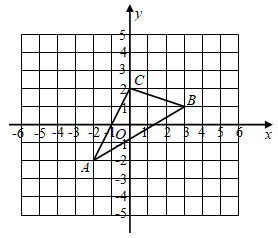 (1)、若把 先向上平移 个单位,再向左平移 个单位得到 ,请写出 、 、 的坐标,并在图中画出平移后图形;(2)、求出三角形 的面积.23. 某学校在疫情期间举行“停课不停学,运动我最棒”为主题的体育活动,并开展了以下体育项目:踢毽子、跳绳、俯卧撑、仰卧起坐,要求每位学生必须且只能选择一项.为了解选择各项体育活动的学生人数,随机抽取了部分学生进行调查,并将获得的数据进行整理,绘制出以下两幅不完整的统计图,请根据统计图回答问题:
(1)、若把 先向上平移 个单位,再向左平移 个单位得到 ,请写出 、 、 的坐标,并在图中画出平移后图形;(2)、求出三角形 的面积.23. 某学校在疫情期间举行“停课不停学,运动我最棒”为主题的体育活动,并开展了以下体育项目:踢毽子、跳绳、俯卧撑、仰卧起坐,要求每位学生必须且只能选择一项.为了解选择各项体育活动的学生人数,随机抽取了部分学生进行调查,并将获得的数据进行整理,绘制出以下两幅不完整的统计图,请根据统计图回答问题: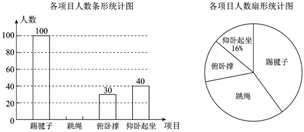 (1)、这次活动一共调查了名学生;(2)、补全条形统计图;(3)、求选择踢毽子项目的人数在扇形统计图中对应的圆心角度数;(4)、若该学校有 人,请你估计学校选择仰卧起坐项目的学生人数约是多少人.24. 某商店计划购买甲、乙两种商品.若购买 件甲商品和 件乙商品共需用 元;若购买 件甲商品和 件乙商品共需用 元.(1)、求每件甲商品和每件乙商品进货价格各多少元;(2)、若该商店甲、乙两种商品共进货 件,要求两种商品的进货总价不高于 元,同时每件甲商品按进价提高 后的销售价格,每件乙商品按进价提高 后的价格销售,两种商品完全售完后的销售总额不低于 元,问该商店共有几种进货方案?25. 已知:任何一个三角形都满足三角形三内角和等于 ,我们把这个结论称之为三角形三内角和定理.如图1, ,且 ,请根据题目条件,结合三角形三内角和定理,探究下列问题:
(1)、这次活动一共调查了名学生;(2)、补全条形统计图;(3)、求选择踢毽子项目的人数在扇形统计图中对应的圆心角度数;(4)、若该学校有 人,请你估计学校选择仰卧起坐项目的学生人数约是多少人.24. 某商店计划购买甲、乙两种商品.若购买 件甲商品和 件乙商品共需用 元;若购买 件甲商品和 件乙商品共需用 元.(1)、求每件甲商品和每件乙商品进货价格各多少元;(2)、若该商店甲、乙两种商品共进货 件,要求两种商品的进货总价不高于 元,同时每件甲商品按进价提高 后的销售价格,每件乙商品按进价提高 后的价格销售,两种商品完全售完后的销售总额不低于 元,问该商店共有几种进货方案?25. 已知:任何一个三角形都满足三角形三内角和等于 ,我们把这个结论称之为三角形三内角和定理.如图1, ,且 ,请根据题目条件,结合三角形三内角和定理,探究下列问题: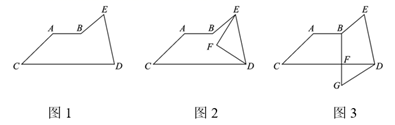 (1)、如图2,在图1基础上作: , , 与 交于点 ,求 的度数;(2)、如图3,在图1基础上作:过 作 ,交 于点 ,且 ,求 的值.26. 如图1,直线 分别交 轴, 轴于点 , ,且 , 满足 .
(1)、如图2,在图1基础上作: , , 与 交于点 ,求 的度数;(2)、如图3,在图1基础上作:过 作 ,交 于点 ,且 ,求 的值.26. 如图1,直线 分别交 轴, 轴于点 , ,且 , 满足 .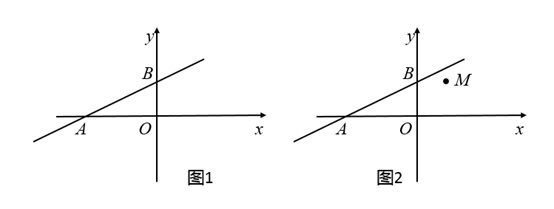 (1)、直接写出 , ;(2)、如图1,点 为直线 上一动点,即点 可以代表为直线 上任意一点,也就是说直线 上的任意一点都可以用点 来表示,且点 的横坐标 和纵坐标 满足等式 .若 ,求点 的坐标;(3)、如图2,在图1基础上,坐标平面内有一点 满足 .现将直线 沿 轴正方向平移 个单位长度后恰好经过点 ,请直接写出 的取值范围.
(1)、直接写出 , ;(2)、如图1,点 为直线 上一动点,即点 可以代表为直线 上任意一点,也就是说直线 上的任意一点都可以用点 来表示,且点 的横坐标 和纵坐标 满足等式 .若 ,求点 的坐标;(3)、如图2,在图1基础上,坐标平面内有一点 满足 .现将直线 沿 轴正方向平移 个单位长度后恰好经过点 ,请直接写出 的取值范围.