2021-2022学年人教版八年级数学上册第十四章整式的乘法与因式分解单元测试卷

试卷更新日期：2021-08-16 类型：单元试卷

进入出卷网下载

一、单选题

1. 下列各式计算结果是a⁶的是（）

A、a³+a³ B、a¹²÷a² C、a²•a³ D、（﹣a³）²

查看试题解析
2. 计算[(a＋b)²]³·(a＋b)³的结果是（）

A、(a＋b)⁸ B、(a＋b)⁹ C、(a＋b)¹⁰ D、(a＋b)¹¹

查看试题解析
3. 下列是某同学在一次作业中的计算摘录：
①3a+2b=5ab，②4m³n-5mn³=-m³n，③4x³•（-2x²）=-6x⁵ ， ④4a³b÷（-2a²b）=-2a，⑤（a³）²=a⁵ ， ⑥（-a）³÷（-a）=-a² ，其中正确的个数有（　　）

A、1个 B、2个 C、3个 D、4个

查看试题解析
4. 计算：（2xy²）⁴•（-6x²y）÷（-12x³y²）的结果为（　　）

A、16x³y⁷ B、4x³y⁷ C、8x³y⁷ D、8x²y⁷

查看试题解析
5. 下列从左到右的变形，属于因式分解的是（）

A、 $(x + 1) (x - 1) = x^{2} - 1$ B、 $m^{2} + m - 4 = (m + 3) (m - 2) + 2$ C、 $x^{2} + 2 x = x (x + 2)$ D、 $x^{2} - 4 y^{2} = (x + 4 y) (x - 4 y)$

查看试题解析
6. 若a，b，c是三角形的三边，则代数式（a-b）²-c²的值是（）

A、正数 B、负数 C、等于零 D、不能确定

查看试题解析
7. 下列多项式，能用平方差公式分解因式的是（）

A、 $x^{2} - x y$ B、 $x^{2} + x y$ C、 $- x^{2} + y^{2}$ D、 $x^{2} + y^{2}$

查看试题解析
8. 已知：a=2014x+2015，b=2014x+2016，c=2014x+2017，则a²+b²+c²﹣ab﹣ac﹣bc的值是（）

A、0 B、1 C、2 D、3

查看试题解析
9. 若x ， y为正整数，且2^x•2^y=2⁵ ，则x ， y的值有（　　）

A、4对 B、3对 C、2对 D、1对

查看试题解析
10. 不论x、y为什么实数，代数式x²+y²+2x﹣4y+7的值（）

A、总不小于2 B、总不小于7 C、可为任何实数 D、可能为负数

查看试题解析

二、填空题

11. 计算：（2ab²）³=

查看试题解析
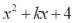12. 若是一个完全平方式，则常数k的值为．

查看试题解析
13. 计算： ${(- 4)}^{2020} \times {0.25}^{2019} =$ ．

查看试题解析
14. 计算：123²-124×122=.

查看试题解析
15. 已知x+y＝3，xy＝－2，则代数式x²y+xy²的值为．

查看试题解析
16. 已知一个长方形的面积是 $6 a^{2} - 4 a b + 2 a$ ，且它的一条边长为 $2 a$ ，则长方形的周长为．

查看试题解析
17. 如果（2a＋2b＋1）（2a＋2b－1）＝63，那么a＋b的值为．

查看试题解析
18. 如图，有两个正方形A，B，现将B放在A的内部得图甲，将A，B并列放置后构造新的正方形得图乙．若图甲和图乙中阴影部分的面积分别为3和15，则正方形A，B的面积之和为．

查看试题解析

三、解答题

19. 计算

(1)、（12a³-6a²+3a）÷3a-1

(2)、（2x+y+z)(2x-y-z)

查看试题解析
20. 因式分解：

(1)、 $4 x^{2} - 8 x y + 2 x$

(2)、 $3 x (a - b) - 6 y (b - a)$

(3)、 $2 a^{3} - 8 a$

(4)、 ${(x^{2} + 4)}^{2} - 16 x^{2}$

查看试题解析
21. 先化简，再求值： $(x^{2} y - 2 x y^{2} - y^{3}) \div y - (x + y) (x - y)$ ，其中 $x = \frac{1}{2}, y = 1$

查看试题解析
22. 若△ABC的三边长a、b、c满足6a+8b+10c﹣50=a²+b²+c² ，试判断△ABC的形状．

查看试题解析
23. 若(x² +mx－8)(x²－3x+n)的展开式中不含 x²和 x³项，求 m和 n的值.

查看试题解析
24. 小马、小虎两人共同计算一道题：（x+a）（2x+b）.由于小马抄错了a的符号，得到的结果是2x²﹣7x+3，小虎漏抄了第二个多项式中x的系数得到的结果是x²+2x﹣3.

(1)、求a，b的值；

(2)、细心的你请计算这道题的正确结果；

(3)、当x＝﹣1时，计算（2）中的代数式的值.

查看试题解析
25.
请认真观察图形，解答下列问题：

（1）根据图中条件，用两种方法表示两个阴影图形的面积的和（只需表示，不必化简）；
（2）由（1），你能得到怎样的等量关系？请用等式表示；
（3）如果图中的 $a ， b$ （ $a$ ＞ $b$ ）满足 $a^{2} + b^{2} = 53$ ， $a b = 14$ ，求：① $a + b$ 的值；② $a^{4} - b^{4}$ 的值.

查看试题解析

2021-2022学年人教版八年级数学上册第十四章 整式的乘法与因式分解 单元测试卷

一、单选题

二、填空题

三、解答题

2021-2022学年人教版八年级数学上册第十四章整式的乘法与因式分解单元测试卷