2021-2022学年人教版八年级数学上册第十三章 轴对称 单元测试卷
试卷更新日期:2021-08-16 类型:单元试卷
一、单选题
-
1. 下列图形中,是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 如图,∠A=30°,∠C′=60°,△ABC 与△A′B′C′关于直线l对称,则∠B度数为( )
2. 如图,∠A=30°,∠C′=60°,△ABC 与△A′B′C′关于直线l对称,则∠B度数为( )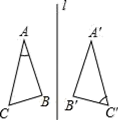 A、 B、 C、 D、3. 如图,将△ABC的三个顶点坐标的横坐标都乘以-1,并保持纵坐标不交,则所得图形与原图形的关系是( )
A、 B、 C、 D、3. 如图,将△ABC的三个顶点坐标的横坐标都乘以-1,并保持纵坐标不交,则所得图形与原图形的关系是( )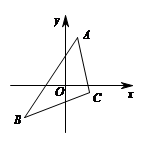 A、关于x轴对称 B、关于y轴对称 C、将原图形沿x轴的负方向平移了1个单位 D、将原图形沿y轴的负方向平移了1个单位4. 已知点P(a, )与点Q关于x轴对称,则点Q的坐标是( )A、Q (a, ) B、Q ( , ) C、Q (a, ) D、Q ( , )5. 有下列命题:①等腰三角形的角平分线、中线和高重合;②等腰三角形两腰上的高相等;③有个外角等于120°的等腰三角形是等边三角形;④等边三角形的高线、中线、角平分线都相等;其中正确的有( )A、1个 B、2个 C、3个 D、4个6. 如图,在 正方形网格中,已将图中的四个小正方形涂上阴影,若再从图中选一个涂上阴影,使得整个阴影部分组成的图形是轴对称图形,那么不符合条件的小正方形是( )
A、关于x轴对称 B、关于y轴对称 C、将原图形沿x轴的负方向平移了1个单位 D、将原图形沿y轴的负方向平移了1个单位4. 已知点P(a, )与点Q关于x轴对称,则点Q的坐标是( )A、Q (a, ) B、Q ( , ) C、Q (a, ) D、Q ( , )5. 有下列命题:①等腰三角形的角平分线、中线和高重合;②等腰三角形两腰上的高相等;③有个外角等于120°的等腰三角形是等边三角形;④等边三角形的高线、中线、角平分线都相等;其中正确的有( )A、1个 B、2个 C、3个 D、4个6. 如图,在 正方形网格中,已将图中的四个小正方形涂上阴影,若再从图中选一个涂上阴影,使得整个阴影部分组成的图形是轴对称图形,那么不符合条件的小正方形是( ) A、① B、② C、③ D、④7. 如图,在△ABC中,AB=AC,∠BAC=120°,AB的垂直平分线交AB于点E,交BC于点F,连接AF,则∠AFC的度数( )
A、① B、② C、③ D、④7. 如图,在△ABC中,AB=AC,∠BAC=120°,AB的垂直平分线交AB于点E,交BC于点F,连接AF,则∠AFC的度数( ) A、 B、 C、 D、8. 如图,△ABC中,AB =AC,过点A作DA⊥AC交BC于点 D .若∠B=2∠BAD,则∠BAD的度数为( )
A、 B、 C、 D、8. 如图,△ABC中,AB =AC,过点A作DA⊥AC交BC于点 D .若∠B=2∠BAD,则∠BAD的度数为( )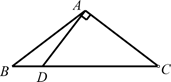 A、18° B、20° C、30° D、36°9. 如图,在 中,AB=AC,AD是BC边的中线,以AC为边作等边△ACE,BE与AD相交于点P,点F在BE上,且PF=PA,连接AF下列四个结论:①AD⊥BC;②∠ABE=∠AEB;③∠APE=60°;④△AEF≌△ABP,其中正确结论的个数是( )
A、18° B、20° C、30° D、36°9. 如图,在 中,AB=AC,AD是BC边的中线,以AC为边作等边△ACE,BE与AD相交于点P,点F在BE上,且PF=PA,连接AF下列四个结论:①AD⊥BC;②∠ABE=∠AEB;③∠APE=60°;④△AEF≌△ABP,其中正确结论的个数是( )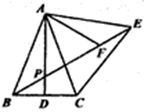 A、 B、 C、 D、10. 如图,等边 的边长为 是 边上的中线, 是 边上的动点, 是 边上一点,若 ,当 取得最小值时,则 的度数为( )
A、 B、 C、 D、10. 如图,等边 的边长为 是 边上的中线, 是 边上的动点, 是 边上一点,若 ,当 取得最小值时,则 的度数为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 黑体汉字中的“中”“田”“日”等都是轴对称图形,请至少再写出三个具有这种特征的汉字:.12. 小明从镜子里看到镜子对面电子钟的像,如图所示,实际时间是
 13. 如图,在△ABC中,AB=AC,D为BC上一点,且CD=AD ,AB=BD,则∠B的度数为 .
13. 如图,在△ABC中,AB=AC,D为BC上一点,且CD=AD ,AB=BD,则∠B的度数为 .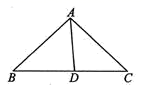 14. 若点A(m+2,3)与点B(﹣4,n+5)关于y轴对称,则m+n=15. 如图,在△ABC中,∠ABC和∠ACB的平分线交于点E,过点E作MN∥BC交AB于M,交AC于N,若BM+CN=9,则线段MN的长为 .
14. 若点A(m+2,3)与点B(﹣4,n+5)关于y轴对称,则m+n=15. 如图,在△ABC中,∠ABC和∠ACB的平分线交于点E,过点E作MN∥BC交AB于M,交AC于N,若BM+CN=9,则线段MN的长为 . 16. 如图,△ABC中,AB=AC,AB的垂直平分线交边AB于D点,交边AC于E点,若△ABC与△EBC的周长分别是40cm,24cm,则AB=cm.
16. 如图,△ABC中,AB=AC,AB的垂直平分线交边AB于D点,交边AC于E点,若△ABC与△EBC的周长分别是40cm,24cm,则AB=cm.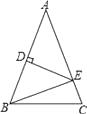 17. 如图,等腰三角形ABC底边BC的长为4 cm,面积是12 cm2 , 腰AB的垂直平分线EF交AG于点F,若D为BC边上的中点,M为线段EF上一动点,则△BDM的周长最短为cm.
17. 如图,等腰三角形ABC底边BC的长为4 cm,面积是12 cm2 , 腰AB的垂直平分线EF交AG于点F,若D为BC边上的中点,M为线段EF上一动点,则△BDM的周长最短为cm. 18. 如图,△ABC 中, AB=11 , AC= 5 ,∠ BAC 的平分线 AD 与边 BC 的垂直平分线 CD 相 交于点 D ,过点 D 分别作 DE⊥AB ,DF⊥AC ,垂足分别为 E 、F ,则 BE 的长为 .
18. 如图,△ABC 中, AB=11 , AC= 5 ,∠ BAC 的平分线 AD 与边 BC 的垂直平分线 CD 相 交于点 D ,过点 D 分别作 DE⊥AB ,DF⊥AC ,垂足分别为 E 、F ,则 BE 的长为 .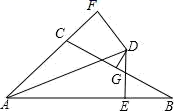
三、解答题
-
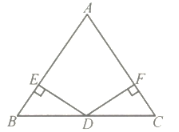
19. 若点M(1,a)与点N(b﹣5,2)关于x轴对称,求a+b的值.20. 如图,在△ABC中,AB=AC,BD=CD,DE AB,DF AC,垂足分别为E,F.求证:DE=DF
 21. 作图:已知∠AOB,试在∠AOB内确定一点P,使P到OA、OB的距离相等,并且到M、N两点的距离也相等。
21. 作图:已知∠AOB,试在∠AOB内确定一点P,使P到OA、OB的距离相等,并且到M、N两点的距离也相等。 22. 如图,图中的小方格都是边长为1的正方形,
22. 如图,图中的小方格都是边长为1的正方形,
①直接写出△ABC的各顶点坐标:
A( , ),B ( , ) ,C ( , ) ;
②画出△ABC关于y轴的对称图形△A1B1C1;
③直接写出△ABC关于x轴对称的△A2B2C2的顶点A2 ( , ) B2 ( , ) (其中A2与A对应,B2与B对应,不必画图.)
23. 某班举行文艺晚会,桌子摆成两直条(如图中的AO,BO),AO桌面上摆满了桔子。BO桌面上摆满了糖果,坐在C处的学生小明先拿桔子再拿糖果,然后回到空座位D上.请你帮助他设计一条行走路线,使其所走的总路程最短?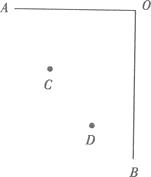 24. 数学课上,张老师举了下面的例题:
24. 数学课上,张老师举了下面的例题:例1:在等腰三角形ABC中,∠A = 100°,求∠B的度数.(答案:40°)
例2:在等腰三角形ABC中,∠A = 50°,求∠B的度数.(答案:50°或65°或80°)
张老师启发同学们进行变式,小敏编了如下一题:
变式:在等腰三角形ABC中,∠A = 70°,求∠B的度数.
(1)、请你解答小敏编的变式题.(2)、解答(1)后小敏发现,∠A的度数不同得到∠B的度数的个数也可能不同.如果在等腰三角形ABC中,设∠A = x°,当∠B有三个不同的度数时,请你探索x的取值范围.25. 如图 (1)、如图①所示,在△ABC中,AB=AC,∠BAC=120°,AD是BC边的中线,DE⊥AB,垂足为E,求证:AB=4AE.(2)、如图②所示,在等边△ABC中,D、E分别是BC、AC上的点,且AE=CD,AD、BE交于点P,作BQ⊥AD于Q,若BP=2,求PQ的长.26. 如图,在△ABC中,AB=BC=AC=12cm,点D为AB上的点,且BD= AB,如果点P在线段BC上以3cm/s的速度由B点向终点C运动,同时,点Q在线段CA上由C点向终点A运动.当一点到达终点时,另一点也随之停止运动.
(1)、如图①所示,在△ABC中,AB=AC,∠BAC=120°,AD是BC边的中线,DE⊥AB,垂足为E,求证:AB=4AE.(2)、如图②所示,在等边△ABC中,D、E分别是BC、AC上的点,且AE=CD,AD、BE交于点P,作BQ⊥AD于Q,若BP=2,求PQ的长.26. 如图,在△ABC中,AB=BC=AC=12cm,点D为AB上的点,且BD= AB,如果点P在线段BC上以3cm/s的速度由B点向终点C运动,同时,点Q在线段CA上由C点向终点A运动.当一点到达终点时,另一点也随之停止运动. (1)、如(图一)若点Q的运动速度与点P的运动速度相等,经过1s后,△BPD与△CQP是否全等,请说明理由.(2)、如(图二)若点Q的运动速度与点P的运动速度相等(点P不与点B和点C重合),连接点A与点P,连接点B与点Q,并且线段AP,BQ相交于点F,求∠AFQ的度数.(3)、若点Q的运动速度为6cm/s,当点Q运动几秒后,可得到等边△CQP?
(1)、如(图一)若点Q的运动速度与点P的运动速度相等,经过1s后,△BPD与△CQP是否全等,请说明理由.(2)、如(图二)若点Q的运动速度与点P的运动速度相等(点P不与点B和点C重合),连接点A与点P,连接点B与点Q,并且线段AP,BQ相交于点F,求∠AFQ的度数.(3)、若点Q的运动速度为6cm/s,当点Q运动几秒后,可得到等边△CQP?