天津市和平区2020-2021学年八年级下学期数学期末试卷
试卷更新日期:2021-08-16 类型:期末考试
一、单选题
-
1. 若 在实数范围内有意义,则 的取值范围是( )A、 B、 C、 D、2. 下列计算正确的是( )A、 B、 C、 D、3. 在下列由线段 , , 的长为三边的三角形中,不能构成直角三角形的是( )A、 , , B、 , , C、 , , D、 , ,4. 已知菱形的两条对角线的长分别是 和 ,则菱形的面积是( )A、 B、 C、 D、5. 在“争创美丽校园”示范校评比活动中,10位评委给某校的评分情况如下表所示:
评分(分)
评委人数
则这10位评委评分的平均数是( )
A、85 B、87.5 C、89 D、906. 有四组数据:第一组
第二组
第三组
第四组
这四组数据的平均数都是 ,方差分别是 , , , ,则这四组数据中波动较大的是( )
A、第一组 B、第二组 C、第三组 D、第四组7. 已知直线 ,则( )A、该直线与 轴的交点坐标为 ,与 轴的交点坐标为 B、该直线与 轴的交点坐标为 ,与 轴的交点坐标为 C、该直线与 轴的交点坐标为 ,与 轴的交点坐标为 D、该直线与 轴的交点坐标为 ,与 轴的交点坐标为8. 一次函数y=x+2的图象不经过的象限是( )A、一 B、二 C、三 D、四9. 在四边形 中,对角线 , 相交于点 ,则下列说法正确的是( )A、如果 , ,那么四边形 是平行四边形 B、如果 , ,那么四边形 是矩形 C、如果 , ,那么四边形 是菱形 D、如果 , , , ,那么四边形 是正方形10. 已知点 , ,点 ,过点 作 轴的平行线交直线 于点 ,则线段 的长为( )A、 B、 C、 D、11. 均匀地向如图中的容器注水,最后把容器注满,在注水过程中,水面高度 随时间 的变化的图象是( ) A、
A、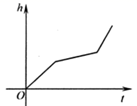 B、
B、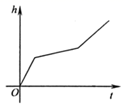 C、
C、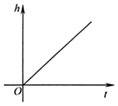 D、
D、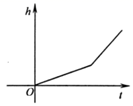 12. 某市政府决定实施供暖改造工程.现甲、乙两工程队分别同时开挖两条 米长的管道,所挖管道长度 (米)与挖掘时间 (天)之间的关系如图所示,则下列说法错误的是( )
12. 某市政府决定实施供暖改造工程.现甲、乙两工程队分别同时开挖两条 米长的管道,所挖管道长度 (米)与挖掘时间 (天)之间的关系如图所示,则下列说法错误的是( ) A、甲队每天挖 米 B、乙队开挖两天后,每天挖 米 C、甲队比乙队提前 天完成任务 D、当 时,甲、乙两队所挖管道长度相同
A、甲队每天挖 米 B、乙队开挖两天后,每天挖 米 C、甲队比乙队提前 天完成任务 D、当 时,甲、乙两队所挖管道长度相同二、填空题
-
13. 计算 的结果等于 .14. 如图,点 , 分别是 的 , 边的中点.若 ,则 的长等于 .
 15. 某校规定:学生的数学学科学期综合成绩是由平时、期中和期末三项成绩按 的比例计算所得.若某同学本学期数学学科的平时、期中和期末成绩分别是 分, 分和 分,则他本学期数学学科学期综合成绩是分.16. 若正比例函数 ( 为常数,且 )的函数值 随着 的增大而增大,则 的值可以是(写出一个即可).17. 如图, ,正方形 的边长为 ,点 到 的距离是 ,则
15. 某校规定:学生的数学学科学期综合成绩是由平时、期中和期末三项成绩按 的比例计算所得.若某同学本学期数学学科的平时、期中和期末成绩分别是 分, 分和 分,则他本学期数学学科学期综合成绩是分.16. 若正比例函数 ( 为常数,且 )的函数值 随着 的增大而增大,则 的值可以是(写出一个即可).17. 如图, ,正方形 的边长为 ,点 到 的距离是 ,则 (1)、正方形 的对角线的长=;(2)、点 到 的距离=;(3)、点 到 的距离= .
(1)、正方形 的对角线的长=;(2)、点 到 的距离=;(3)、点 到 的距离= .三、解答题
-
18. 在每个小正方形的边长为 的网格中,点 , 在格点上.请用无刻度的直尺,按下列要求画图.
 (1)、在图①画出一个以 为一边的正方形 ;(2)、在图②画出一个以 为一边的菱形 ( 不是正方形);(3)、如图③,点 , 在格点上, 与 交于点 ,在图③中画出一个以 为一边的矩形 .19.(1)、 ;(2)、 .20. 在一次中学生田径运动会上,根据参加男子跳高初赛的运动员的成绩(单位: ),绘制出如下的统计图①和图②.请根据相关信息,解答下列问题:
(1)、在图①画出一个以 为一边的正方形 ;(2)、在图②画出一个以 为一边的菱形 ( 不是正方形);(3)、如图③,点 , 在格点上, 与 交于点 ,在图③中画出一个以 为一边的矩形 .19.(1)、 ;(2)、 .20. 在一次中学生田径运动会上,根据参加男子跳高初赛的运动员的成绩(单位: ),绘制出如下的统计图①和图②.请根据相关信息,解答下列问题:
 (1)、图①中 的值为 .(2)、求统计的这组初赛成绩数据的平均数、众数和中位数;(3)、根据这组初赛成绩,由高到低确定 人能进入复赛,请直接写出初赛成绩为 的运动员能否进入复赛.21. 如图,在 中, , , 为 边上一点,且 .
(1)、图①中 的值为 .(2)、求统计的这组初赛成绩数据的平均数、众数和中位数;(3)、根据这组初赛成绩,由高到低确定 人能进入复赛,请直接写出初赛成绩为 的运动员能否进入复赛.21. 如图,在 中, , , 为 边上一点,且 . (1)、 的大小=;(2)、斜边 的长=;(3)、斜边 上的中线的长=;(4)、求 的长.22. 已知,在四边形 中, , .
(1)、 的大小=;(2)、斜边 的长=;(3)、斜边 上的中线的长=;(4)、求 的长.22. 已知,在四边形 中, , . (1)、如图①,求证: ;(2)、如图②,四边形 的对角线 平分 .求证:四边形 是菱形.23. 在抗洪抢险救灾中,某地粮食局为了保证库存粮食的安全,决定将甲、乙两个仓库的粮食,全部转移到没有受洪水威胁的 , 两个仓库.已知甲库有粮食100吨,乙库有粮食80吨,而 库的容量为60吨, 库的容量为120吨.(1)、填空:
(1)、如图①,求证: ;(2)、如图②,四边形 的对角线 平分 .求证:四边形 是菱形.23. 在抗洪抢险救灾中,某地粮食局为了保证库存粮食的安全,决定将甲、乙两个仓库的粮食,全部转移到没有受洪水威胁的 , 两个仓库.已知甲库有粮食100吨,乙库有粮食80吨,而 库的容量为60吨, 库的容量为120吨.(1)、填空:若从甲库运往 库粮食50吨,
①从甲库运往 库粮食吨;
②从乙库运往 库粮食吨;
③从乙库运往 库粮食吨;
(2)、填空:若从甲库运往 库粮食 吨,
①从甲库运往 库粮食吨;
②从乙库运往 库粮食吨;
③从乙库运往 库粮食吨;
(3)、从甲、乙两库到 , 两库的路程和运费如表:(表中“元/吨·千米”表示每吨粮食运送 千米所需人民币)路程(千米)
运费(元/吨·千米)
甲库
乙库
甲库
乙库
库
库
写出将甲、乙两库粮食运往 , 两库的总运费 (元)与 (吨)的函数关系式.并求出当从甲、乙两库各运往 , 两库多少吨粮食时,总运费最省,最省的总运费是多少?
24. 已知正方形 的边长为 ,点 是对角线 上的一点. (1)、如图①,若点 到 的距离为 ,则点 到 的距离为;(2)、连接 ,过点 作 ,交 于点 .
(1)、如图①,若点 到 的距离为 ,则点 到 的距离为;(2)、连接 ,过点 作 ,交 于点 .①如图②,以 , 为邻边作矩形 .求证:矩形 是正方形;
②如图③,在①的条件下,连接 ,求 的值;
③点 恰为 的中点,连接 交 于点 ,则 的长= .
25. 如图,在平面直角坐标系中,点 ,点 ,点 关于 轴的对称点为 . (1)、点 的坐标为;(2)、已知一次函数的图象经过点 与 ,求这个一次函数的解析式;(3)、点 是 轴上的一个动点,当 时, 的周长最小;(4)、点 , 是 轴上的两个动点,当 时,四边形 的周长最小;(5)、点 ,点 分别是 轴和 轴上的动点,当四边形 的周长最小时, , 此时四边形 的面积为 .
(1)、点 的坐标为;(2)、已知一次函数的图象经过点 与 ,求这个一次函数的解析式;(3)、点 是 轴上的一个动点,当 时, 的周长最小;(4)、点 , 是 轴上的两个动点,当 时,四边形 的周长最小;(5)、点 ,点 分别是 轴和 轴上的动点,当四边形 的周长最小时, , 此时四边形 的面积为 .