上海市徐汇区2020-2021学年八年级下学期数学期末试卷

试卷更新日期：2021-08-16 类型：期末考试

进入出卷网下载

一、单选题

1. 一次函数 $y = - 2 x + 1$ 的图象经过哪几个象限（）

A、一、二、三象限 B、一、二、四象限 C、一、三、四象限 D、二、三、四象限

查看试题解析
2. 下列方程，有实数解的是（）

A、 $\sqrt{x - 2} + 1 = 0$ B、 $\frac{x}{x - 2} = \frac{2}{x - 2}$ C、 ${(x + 2)}^{4} - 1 = 0$ D、 $\sqrt{x - 4} + \sqrt{x - 3} = 0$

查看试题解析
3. 如果 $\overset{⇀}{E F} = \overset{⇀}{M N}$ ，那么下列结论中正确的是（）

A、 $| \vec{E N} | = | \vec{F M} |$ B、 $\bar{E M}$ 与 $\bar{F N}$ 是相等向量 C、 $\bar{E N}$ 与 $\vec{M F}$ 是相反向量 D、 $\bar{E N}$ 与 $\vec{M F}$ 是平行向量

查看试题解析
4. 下列语句所描述的事件中，是不可能事件的是（）

A、锄禾日当午 B、大漠孤烟直 C、手可摘星辰 D、黄河入海流

查看试题解析
5. 下列图形中，是中心对称但不是轴对称图形的是（）

A、菱形 B、矩形 C、等腰梯形 D、平行四边形

查看试题解析
6. 已知四边形 $A B C D$ 中， $A B / / C D ， A C = B D$ ，下列判断中的正确的是（）

A、如果 $B C = A D$ ，那么四边形 $A B C D$ 是等腰梯形 B、如果 $A D / / B C$ ，那么四边形 $A B C D$ 是菱形 C、如果AC平分BD，那么四边形 $A B C D$ 是矩形 D、如果 $A C ⊥ B D$ ，那么四边形 $A B C D$ 是正方形

查看试题解析

二、填空题

7. 将直线 $y = - x - 2$ 沿 $y$ 轴方向向上平移3个单位，所得新图像的函数表达式是．

查看试题解析
8. 已知一次函数 $y = m x + 1 (m \neq 0)$ ，若y的值随x的增大而增大，则m的取值范围是．

查看试题解析
9. 方程 $\frac{1}{2} x^{3} + 4 = 0$ 的解是．

查看试题解析
10. 方程 $\sqrt{2 - x} = 3$ 的解是．

查看试题解析
11. 已知一次函数 $y = k x + b$ （ $k \neq 0$ ）的图像如图所示，那么关于 $x$ 的不等式 $k x + b > 0$ 的解集是．

查看试题解析
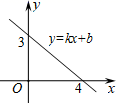12. 如果关于 $x$ 是方程 $x^{2} - x + m = 0$ 有两个相等的实数根，那么 $m$ 的值等于．

查看试题解析
13. 一个n边形的内角和是540°，那么n= ．

查看试题解析
14. 用换元法解方程 $\frac{x - 1}{x^{2}} + \frac{2 x^{2}}{x - 1} = 3$ 时，如果设 $y = \frac{x - 1}{x^{2}}$ ，那么原方程化成关于 $y$ 的整式方程是

查看试题解析
15. 我们古代《四元玉鉴》中记载“二果问价”问题，其内容如下：“九百九十九文钱，甜果苦果共买千，甜果九个十一文，苦果七个四文钱，试问甜苦果几个，又问各该几个钱？”如果设买甜果 $x$ 个，买苦果 $y$ 个，那么列出的关于 $x ， y$ 的二元一次方程组是．

查看试题解析
16. 已知，如图，边长为4的正方形 $A B C D$ 中，点 $E 、 F$ 分别在 $C A 、 A C$ 的延长线上，且 $∠ B E D = ∠ B F D = 45 °$ ，那么四边形 $E B F D$ 的面积是．

查看试题解析
17. 我们把联结四边形对边中点的线段称为“中对线”．凸四边形 $A B C D$ 的对角线 $A C = B D = 12$ ，且这两条对角线的夹角为60°，那么该四边形较长的“中对线”的长度为．

查看试题解析
18. 已知等边 $Δ A B C$ 的边长为 $6 ， D$ 是边 $A B$ 上一点，DE∥BC交边 $A C$ 于点 $E$ ，以 $D E$ 为一边在 $Δ A B C$ 形内构造矩形DEFG．且 $D G = \frac{1}{2} D E$ ．设 $A D = x ， B G = y$ ，则 $y$ 关于 $x$ 的函数关系式是（无需写出定义域）．

查看试题解析

三、解答题

19. 解方程组： ${\begin{matrix} x^{2} - 5 x y - 6 y^{2} = 0 \\ x^{2} - 4 x y + 4 y^{2} = 1 \end{matrix}$ ．

查看试题解析
20. 如图， $▱ A B C D$ 的对角线 $A C 、 B D$ 相交于点 $O$ ．点 $E$ 在对角线 $B D$ 的延长线上，且 $D E = O D$ ．

(1)、图中与 $\vec{O B}$ 相等的向量是；

(2)、计算： $\vec{A E} - \vec{A D} + \vec{B A}$ ；

(3)、在图中求作 $\vec{A E} - \vec{C O}$ ．（保留作图痕迹，不要求写作法，请指出哪个向量是所求作的向量）

查看试题解析
21. 小明和小杰从同一地点去青浦郊野公园，小明坐公交车去，小杰因为有事晚出发，乘出租车以1.6千米/分钟的平均速度沿路追赶．图中 $l_{1}$ ， $l_{2}$ 分别表示公交车与出租车在行驶中的路程（千米）与时间（分钟）的关系，根据图像解决下列问题：

(1)、小明早到了分钟，公交车的平均速度为千米/分钟；

(2)、小杰路上花费的时间是分钟，比小明晚出发分钟；

(3)、求出租车行驶过程中s与t的函数关系式，并写出定义域．

查看试题解析
22. 小杰和小明玩扑克牌游戏，各出一张牌比输赢．游戏的规则是：谁的牌数字大谁赢，同样大就平：A遇2就输，遇其他牌（除A外）都赢．目前小杰手中A、K、J，小明手中有2、Q、J．

(1)、求出小明抽到的牌恰好是“2”的概率；

(2)、小杰、小明两人谁获胜的机会大？画出树状图，通过计算说明理由．

查看试题解析
23. 为响应国家号召，全体公民接种疫苗，提高对“新冠”病毒的免疫功能．现某大型社区有6000人需要接种疫苗，为了尽快完成该项任务，防疫部门除固定接种点外还增加了一辆流动疫苗接种车，实际每日接种人数比原计划多了250人，结果提前了2天完成全部接种任务．求原计划每天接种人数是多少？

查看试题解析
24. 如图，已知梯形ABCD中，AD∥BC，E、G分别是AB、CD的中点，点F在边BC上，且 $B F = \frac{1}{2} (A D + B C)$ ．

(1)、求证：四边形AEFG是平行四边形；

(2)、若四边形AEFG是矩形，求证：AG平分∠FAD．

查看试题解析
25. 已知，如图，在平面直角坐标系中，一次函数 $y = - 2 x - 4$ 与 $x$ 轴交于点C，与y轴交于点B，点A为y轴正半轴上的一点，将△ABC绕着顶点B旋转后，点C的对应点C’落在y轴上，点A的对应点A’恰好落在反比例函数 $y = \frac{k}{x} (k \neq 0)$ 的图像上．

(1)、求 $Δ B O C$ 的面积；

(2)、如果 $k$ 的值为6 （即反比例函数为 $y = \frac{6}{x}$ ），求点 $A'$ 的坐标；

(3)、如果四边形 $A C B A^{'}$ 是梯形，求 $k$ 的值．

查看试题解析
26. 已知：正方形ABCD的边长为8，点E是BC边的中点，点F是边AB上的动点，联结DE、EF．

(1)、如图1，如果BF=2，求证：EF⊥DE；

(2)、如图2，如果BF=3，求证：∠DEF=3∠CDE；

(3)、联结DF，设DF的中点为G，四边形AFEG是否可能为菱形？请说明理由．

查看试题解析