上海市浦东新区2020-2021学年八年级下学期数学期末试卷
试卷更新日期:2021-08-16 类型:期末考试
一、单选题
-
1. 一次函数y= - 2x+1的图象不经过的象限是( ).A、.第一象限 B、第二象限 C、第三象限 D、第四象限2. 下列方程中,有一个根是x=2的方程是( )A、 B、 C、 D、3. 下列事件属于必然事件的事( )A、某种彩票的中奖概率为 ,购买 张彩票一定能中奖 B、电视打开时正在播放广告 C、任意两个负数的乘积为正数 D、某人手中的玻璃杯不小心掉在水泥地面上会破碎4. 已知向量 、 满足| |=| |,则( )A、 = B、 =﹣ C、 ∥ D、以上都有可能5. 下列命题中正确的是( )A、对角线互相垂直的平行四边形是正方形 B、一组对边平行,且有一个角是直角,一组邻边相等的四边形是正方形 C、对角线相等且互相垂直的四边形是正方形 D、对角线相等且互相垂直平分的四边形是正方形6. 如图,在梯形 中, , , ,那么下列结论错误的是( )
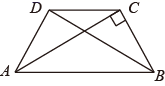 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
7. 如果将函数 的图象向上平移 个单位,那么所得图象的函数解析式是 .8. 关于 的方程 ( )的解为 .9. 已知方程 ,如果设 ,那么原方程可以变形为 .10. 某同学投掷一枚硬币,如果连续 次都是正面朝上,则他第 次抛掷硬币的结果是正面朝上的概率是 .11. 一个多边形的内角和是1800°,这个多边形是边形.12. 计算: .13. 在平行四边形 中, ,则 °.14. 梯形的面积为 平方厘米,中位线长为 厘米,则这个梯形的高为厘米.15. 依次连接菱形各边中点所得到的四边形是 .16. 矩形的较短边长是 ,两条对角线的夹角为 ,则这个矩形的面积是 .17. 在直角梯形 中, , , , ,则 的度数是 .18. 点 在一次函数 的图象上,一次函数与 轴相交于点 , 、 两点关于 轴对称.将 沿 轴左右平移到 ,在平移过程中,将该角绕点 旋转,使它的一边始终经过点 ,另一边与直线 交于点 .若 为等腰直角三角形,且 ,则点 的坐标为 .
三、解答题
-
19. 解方程:20. 解方程组:21. 如图,四边形 是平行四边形, , .
 (1)、填空: ; ;(2)、在图中求作: .(保留作图痕迹,写出结果,不要求写作法);(3)、若 , , ,则 .22. 如图,已知四边形 是平行四边形,将边 延长至点 ,使 ,联结 、 , 与 交于点 .
(1)、填空: ; ;(2)、在图中求作: .(保留作图痕迹,写出结果,不要求写作法);(3)、若 , , ,则 .22. 如图,已知四边形 是平行四边形,将边 延长至点 ,使 ,联结 、 , 与 交于点 . (1)、求证:四边形 是平行四边形;(2)、若 ,求证:四边形 是矩形.23. 如图,在正方形 中, 是对角线 上的一点,点 在边 的延长线上,且 , 交 于点 .
(1)、求证:四边形 是平行四边形;(2)、若 ,求证:四边形 是矩形.23. 如图,在正方形 中, 是对角线 上的一点,点 在边 的延长线上,且 , 交 于点 . (1)、求证: ;(2)、求证: .24. 为庆祝建党100周年,某中学组织八年级学生进行徒步活动,从学校出发,步行至离校 千米的红色基地,返回时,由于步行速度比去时每小时少 千米,结果时间比去时多用了半小时,求学生返回时步行的速度.25. 已知点 、 在反比例函数 的图象上,直线 经过点 、 ,且与 轴、 轴的交点分别为 、 两点.
(1)、求证: ;(2)、求证: .24. 为庆祝建党100周年,某中学组织八年级学生进行徒步活动,从学校出发,步行至离校 千米的红色基地,返回时,由于步行速度比去时每小时少 千米,结果时间比去时多用了半小时,求学生返回时步行的速度.25. 已知点 、 在反比例函数 的图象上,直线 经过点 、 ,且与 轴、 轴的交点分别为 、 两点. (1)、求直线 的解析式;(2)、 为坐标原点,点 在直线上(点 与点 不重合), ,求点 的坐标;(3)、在(2)的条件下,点 在坐标平面上,顺次联结点 、 、 、 的四边形 满足: , ,求满足条件的点 坐标.26. 如图,在菱形 中,对角线 与 相交于点 , , ,点 从点 出发,沿 以每秒 个单位长度的速度向终点 运动,当点 与点 不重合时,过点 作 于点 ,作 交 于点 ,过点 作射线 垂线段 ,垂足为点 ,得到矩形 ,设点 的运动时间为 秒.
(1)、求直线 的解析式;(2)、 为坐标原点,点 在直线上(点 与点 不重合), ,求点 的坐标;(3)、在(2)的条件下,点 在坐标平面上,顺次联结点 、 、 、 的四边形 满足: , ,求满足条件的点 坐标.26. 如图,在菱形 中,对角线 与 相交于点 , , ,点 从点 出发,沿 以每秒 个单位长度的速度向终点 运动,当点 与点 不重合时,过点 作 于点 ,作 交 于点 ,过点 作射线 垂线段 ,垂足为点 ,得到矩形 ,设点 的运动时间为 秒. (1)、求点 与点 重合时 的值;(2)、设矩形 与菱形 重叠部分图形的面积为 ,求 与 之间的函数关系式;(3)、设矩形 的对角线 与 相交于点 ,
(1)、求点 与点 重合时 的值;(2)、设矩形 与菱形 重叠部分图形的面积为 ,求 与 之间的函数关系式;(3)、设矩形 的对角线 与 相交于点 ,①当 时, 的值为 ▲ ;
② 时,求出 的值.