山西省朔州市2020-2021学年八年级下学期数学期末试卷
试卷更新日期:2021-08-16 类型:期末考试
一、单选题
-
1. 将 化成最简二次根式正确的是( )A、 B、 C、 D、2. 已知y是x的正比例函数,当 时, ,则y与x的函数关系式为( )A、 B、 C、 D、3. 甲、乙、丙、丁四人进行射箭测试,每人10次射箭成绩的平均数都是9.1环,方差分别是 , , , ,则射箭成绩最稳定的是( )A、甲 B、乙 C、丙 D、丁4. 我国是最早了解勾股定理的国家之一,早在三千多年前,周朝数学家商高就提出了“勾三、股四、弦五”这一结论,被记载于我国古代一部著名的数学著作中.这部著作是( )A、
 B、
B、 C、
C、 D、
D、 5. 下列运算正确的是( )A、 B、 C、 D、6. 菱形和矩形的对角线,具有的性质是下列的( )A、对角线相等 B、对角线互相垂直 C、对角线互相垂直平分 D、对角线互相平分7. 两个直角三角形拼成如图所示的图形,则 的值为( )
5. 下列运算正确的是( )A、 B、 C、 D、6. 菱形和矩形的对角线,具有的性质是下列的( )A、对角线相等 B、对角线互相垂直 C、对角线互相垂直平分 D、对角线互相平分7. 两个直角三角形拼成如图所示的图形,则 的值为( ) A、 B、3 C、 D、58. 如图,在正方形 中,点 是对角线上一点,连接 , ,若 ,则 的度数为( )
A、 B、3 C、 D、58. 如图,在正方形 中,点 是对角线上一点,连接 , ,若 ,则 的度数为( ) A、105° B、120° C、135° D、150°9. 对于一次函数 ( , 为常数,且 )表中给出5组自变量及其对应的函数值,其中只有1个函数值计算有误,则这个错误的函数值是( )
A、105° B、120° C、135° D、150°9. 对于一次函数 ( , 为常数,且 )表中给出5组自变量及其对应的函数值,其中只有1个函数值计算有误,则这个错误的函数值是( )…
0
1
2
3
…
…
1
4
8
10
…
A、1 B、4 C、8 D、1010. 如图,直线 ,直线 与直线 之间的距离为2,直线 与直线 之间的距离为4.正方形 的对角线 与 相交于点 ,若顶点 , , 分别在直线 , , 上,则 的面积为( ) A、5 B、4 C、3 D、2
A、5 B、4 C、3 D、2二、填空题
-
11. 计算 的结果为 .12. 实行垃圾分类,可节约资源、保护环境,是社会文明的一种重要体现.某街道对所属社区垃圾分类开展情况进行考核,考核项目:A“开展垃圾分类宣传教育”,B“生活垃圾分类设施完备”,C“设立垃圾分类监督机制”.“幸福”社区这三个项目考核成绩分别为:80分,90分,85分.各项成绩满分均为100分.若按如图的权重计算各社区的成绩,则“幸福”社区考核成绩为分.
 13. 在平面直角坐标系中,已知一次函数 的图象经过 , 两点,则 , 的大小关系为 .14. 《算法统宗》中有一道“荡秋干”的问题,其译文为:“有一架秋千,当它静止时,踏板上一点A离地1尺,将它往前推送10尺(水平距离)时,点A对应的点B就和某人一样高,若此人的身高为5尺,秋干的绳索始终拉得很直,试问绳素有多长?”根据上述条件,秋干绳索长为尺.
13. 在平面直角坐标系中,已知一次函数 的图象经过 , 两点,则 , 的大小关系为 .14. 《算法统宗》中有一道“荡秋干”的问题,其译文为:“有一架秋千,当它静止时,踏板上一点A离地1尺,将它往前推送10尺(水平距离)时,点A对应的点B就和某人一样高,若此人的身高为5尺,秋干的绳索始终拉得很直,试问绳素有多长?”根据上述条件,秋干绳索长为尺.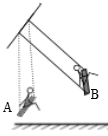 15. 矩形 中, , ,对角线 , 相交于点 ,点 为 上一点,将 沿 折叠,使点 落在对角线 的点 处,则线段 的长为 .
15. 矩形 中, , ,对角线 , 相交于点 ,点 为 上一点,将 沿 折叠,使点 落在对角线 的点 处,则线段 的长为 .
三、解答题
-
16. 计算:(1)、 ;(2)、 .17. 在一次综合实践活动中,老师让同学们测量公园里凉亭A,B之间的距离(A,B之间有水池,无法直接测量).智慧小组的同学们在公园里选了凉亭C,D,测得 , .请你根据上述数据求出A,B之间的距离.
 18. 一次函数 ,它与 轴交于点 ,与 轴交于点 .
18. 一次函数 ,它与 轴交于点 ,与 轴交于点 . (1)、求 , 两点的坐标并在如图的坐标系中画出该一次函数的图象;(2)、根据图象直接写出 时 的取值范围.19. 开展党史学习教育,是党中央因时因势作出的重大决策,是大力推进红色基因传承的重要举措,是凝聚智慧力量奋进新征程的现实需要.某学校在党员教师中开展了学习党史知识竞赛,将参赛的甲,乙两组党员教师成绩整理如下:
(1)、求 , 两点的坐标并在如图的坐标系中画出该一次函数的图象;(2)、根据图象直接写出 时 的取值范围.19. 开展党史学习教育,是党中央因时因势作出的重大决策,是大力推进红色基因传承的重要举措,是凝聚智慧力量奋进新征程的现实需要.某学校在党员教师中开展了学习党史知识竞赛,将参赛的甲,乙两组党员教师成绩整理如下:
整理数据:
甲组:6 7 7 8 9 10 10 10 9 8
乙组:7 5 6 6 10 10 10 9 10 9
分析数据:
组别
平均数(分)
中位数(分)
众数(分)
甲组
8.4
乙组
根据以上信息解答下列问题:
(1)、 , , , , ;(2)、学校计划从每个组选5人代表学校参加区党委组织的党史知识竞赛,甲组张老师的成绩为8分,请从表格中选择合适的统计量判断张老师能否代表学校参加;(3)、请你从“平均数”,“中位数”,“众数”中任选一个角度对甲、乙两组党员的成绩进行评价.20. 如图,四边形 是平行四边形, 的平分线交 边于点 , 的平分线交 边于点 , 和 相交于点 ,连接 . (1)、根据题意将图形补画完整(要求尺规作图,保留作图痕迹,标注相应字母,不写作法);(2)、求证:四边形 是菱形.21. 某经销商销售一种燃气加热器.如图,射线 反映了该加热器的销售收入 (元)与销售量 (台)的关系;射线 反映了该加热器的销售成本 (元)与销售量 (台)之间的关系,其中 ,根据图象解答下列问题:
(1)、根据题意将图形补画完整(要求尺规作图,保留作图痕迹,标注相应字母,不写作法);(2)、求证:四边形 是菱形.21. 某经销商销售一种燃气加热器.如图,射线 反映了该加热器的销售收入 (元)与销售量 (台)的关系;射线 反映了该加热器的销售成本 (元)与销售量 (台)之间的关系,其中 ,根据图象解答下列问题: (1)、射线 对应的函数表达式为;射线 对应的函数表达式为;(2)、图象中射线 与射线 的交点 的坐标为 , 点 坐标表示的实际意义是;(3)、设该经销商销售此加热器所获利润为 (元)(利润=销售收入-销售成本,且 ).
(1)、射线 对应的函数表达式为;射线 对应的函数表达式为;(2)、图象中射线 与射线 的交点 的坐标为 , 点 坐标表示的实际意义是;(3)、设该经销商销售此加热器所获利润为 (元)(利润=销售收入-销售成本,且 ).①求 (元)与销售量 (台)之间的函数关系式,并写出自变量 的取值范围;
②若该经销商销售此种加热器获得了5000元的利润,则共销售了多少台加热器?
22. 阅读与理解:小亮在学习完八年级下册后,结合前面所学知识对“求一元一次方程的解”整理得出以下几种方法,请仔细阅读并完成相应的任务:
数学复习笔记
专题:一元一次方程解法
时间:2021年6月×日
引例:求一元一次方程 的解
方法一:按照七年级解一元一次方程的步骤求解.
移项,合并同类项,未知数系数化1
……
方法二:将方程移项,合并同类项得 ,如图,把此方程的解看成一个一次函数的图象与 轴交点的横坐标,由图可知该方程的解为 .

方法三:方程 的解可以看成两个一次函数 和 的交点的横坐标,由图可知该方程的解为 .

任务:
(1)、方法二和方法三共同体现的一个数学思想是;(只填序号)①数形结合思想;②公理化思想;③分类讨论思想;④整体思想
(2)、依据“方法二”的思路,直接写出图一中对应的一次函数表达式为;(3)、参照“方法三”的思路,求解一元一次方程 的解时,请在图的平面直角坐标系中画出相应的函数图象并依据图象直接写出方程的解. 23. 综合与实践问题情境:一次数学课上,老师出示了课本中的一道复习题:如图, 和 都是等边三角形, 、 分别是 、 上的点,且 ,连接 、 .
23. 综合与实践问题情境:一次数学课上,老师出示了课本中的一道复习题:如图, 和 都是等边三角形, 、 分别是 、 上的点,且 ,连接 、 .

 (1)、初步探究:
(1)、初步探究:试判断 与 的数量关系,并说明理由;
(2)、求证:四边形 是平行四边形;(3)、深入探究:如图2,四边形 和四边形 都是正方形, 、 分别是 、 上的点,且 ,连接 、 ,试判断四边形 的形状,并说明理由;
(4)、拓展延伸:如图3,四边形 和四边形 都是菱形, , , 是 上一点,连接 、 ,延长 交 于 ,若四边形 是平行四边形,请直接写出 的长.