山西省临汾市侯马市2020-2021学年八年级下学期数学期末试卷

试卷更新日期：2021-08-16 类型：期末考试

进入出卷网下载

一、单选题

1. 2020年6月23日，我国北斗卫星导航系统最后一颗组网卫星发射成功，中国北斗卫星导航系统是中国自行研制的全球导航系统，可为用户提供定位、导航、授时服务，定位精度10米，测速精度0.2米/秒，授时精度0.000 000 01秒，数据0.000 000 01用科学记数法表示为（）

A、0.1×10^－7 B、1×10^－8 C、1×10^－9 D、10×10^－8

查看试题解析
2. 在端午节道来之前，双十中学高中部食堂推荐了A，B，C三家粽子专卖店，对全校师生爱吃哪家店的粽子作调查，以决定最终向哪家店采购．下面的统计量中最值得关注的是（）

A、方差 B、平均数 C、中位数 D、众数

查看试题解析
3. 下列条件中，不能判定四边形 $A B C D$ 是平行四边形的是（）

A、 $A B = C D$ ， $∠ A = ∠ B$ B、 $A B ∥ C D$ ， $∠ A = ∠ C$ C、 $A B ∥ C D$ ， $A B = C D$ D、 $A B ∥ C D$ ， $A D ∥ B C$

查看试题解析
4. 一次函数y＝2x+3的图象沿y轴向下平移2个单位，所得图象的函数解析式是（）

A、y＝2x－3 B、y＝2x+2 C、y＝2x+1 D、y＝2x

查看试题解析
5. 在平面中，下列命题为真命题的是（）

A、四个角相等的四边形是矩形 B、对角线垂直的四边形是菱形 C、对角线相等的四边形是矩形 D、四边相等的四边形是正方形

查看试题解析
6. 设函数 $y = \frac{2}{x}$ 与 $y = x - 1$ 的图象的交点坐标为 $(a ， b)$ ，则 $\frac{1}{a} - \frac{1}{b}$ 的值为（）

A、 $- \frac{3}{2}$ B、 $\frac{3}{2}$ C、 $- \frac{1}{2}$ D、 $\frac{1}{2}$

查看试题解析
7. 某校军训期间举行军姿比赛，比赛打分包括以下几项：服装统一，进退场有序，动作规范，动作整齐（每项满分 $10$ 分），已知八年级二班的各项得分如下表：

项目

服装统一

进退场有序

动作规范

动作整齐

得分

$10$

$9$

$8$

$8$

如果将服装统一，进退场有序，动作规范，动作整齐这四项得分依次按 $10 % ， 20 %$ ， $30 % ， 40 %$ 的比例计算比赛成绩，那么八年级二班这次比赛的成绩为（）

A、 $8.75$ B、 $3.5$ C、 $8.4$ D、 $2.1$

查看试题解析
8. 如图，四边形ABCD是平行四边形，点E是边CD上一点，且BC＝EC，CF⊥BE交AB于点F，P是EB延长线上一点，下列结论：①BE平分∠CBF；②CF平分∠DCB；③BC＝FB；④PF＝PC.其中正确结论的个数为（）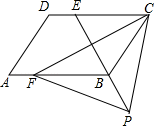

A、1 B、2 C、3 D、4

查看试题解析
9. 如图，把一个长方形的纸片对折两次，然后剪下一个角，为了得到一个钝角为120°的菱形，剪口与第二次折痕所成角的度数应为（）

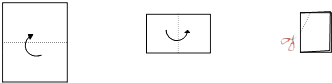A、15°或30° B、30°或45° C、45° 或60° D、30°或60°

查看试题解析
10. 如图，矩形ABCD的边长AB＝6，BC＝8，将矩形沿EF折叠，使点C与点A重合，则折痕EF的长是（）

A、7.5 B、6 C、10 D、5

查看试题解析

二、填空题

11. 计算：（ $\frac{1}{2}$ ）^－1－ $\sqrt{4}$ ＝．

查看试题解析
12. 如图，平行四边形ABCD中，AC与BD交于点O，AE⊥BD于E，BD＝20，BE＝7，AE＝4，则AC的长等于．

查看试题解析
13. 如图，两个完全相同的三角尺ABC和DEF在直线l上滑动．要使四边形CBFE为菱形，还需添加的一个条件是（写出一个即可）．

查看试题解析
14. 一组数据按从小到大的顺序排列为1，2，3，x ， 4，5，若这组数据的中位数为3，则这组数据的方差是．

查看试题解析
15. 如图，已知点 $A$ 为双曲线 $y = - \frac{6}{x} (x < 0)$ 上的一点， $A B ⊥ x$ 轴， $O A = 4$ ，且 $O A$ 的垂直平分线交 $x$ 轴于点 $C$ ，连接 $A C$ ，则 $Δ A B C$ 的周长为．

查看试题解析

三、解答题

16. 先化简： $\frac{2 a + 2}{a - 1}$ ÷（a＋1）＋ $\frac{a^{2} - 1}{a^{2} - 2 a + 1}$ ，然后让a在－1、1、5三个数中选一个合适的数代入求值．

查看试题解析
17. 如图，在菱形ABCD中，AD∥x轴，点A的坐标为（0，3），点B的坐标为（4，0）．CD边所在直线y₁＝mx＋n与x轴交于点C，与双曲线y₂＝ $\frac{k}{x}$ （x＜0）交于点D．

(1)、求直线CD对应的函数解析式及k的值．

(2)、当x＜0时，使y₁－y₂≤0的自变量x的取值范围为．

查看试题解析
18. 今年是中国共产党建党100周年，为了更好地了解党的知识，学校计划用400元购买某种红色经典书籍（每本价格相同），“五一”期间，书店推出优惠政策：该系列丛书8折销售．这样，学校比原计划多买了8本．求每本书的原价和学校实际购买图书的数量．

查看试题解析

19. 为声援扬州“运河申遗”，某校举办了一次运河知识竞赛，满分10分，学生得分为整数，成绩达到6分以上（包括6分）为合格，达到9分以上（包含9分）为优秀．这次竞赛中甲乙两组学生成绩分布的条形统计图如图所示．

(1)、补充完成下面的成绩统计分析表：

组别	平均分	中位数	方差	合格率	优秀率
甲组	6.7		3.41	90%	20%
乙组		7.5	1.69	80%	10%

(2)、小明同学说：“这次竞赛我得了7分，在我们小组中排名属中游略偏上！”观察上表可知，小明是组的学生；（填“甲”或“乙”）

(3)、甲组同学说他们组的合格率、优秀率均高于乙组，所以他们组的成绩好于乙组．但乙组同学不同意甲组同学的说法，认为他们组的成绩要好于甲组．请你给出两条支持乙组同学观点的理由．

查看试题解析

20. 如图，四边形ABCD中，点E在AD上，且EA＝EB，∠ADB＝∠CBD＝90°，∠AEB＋∠C＝180°，求证：

(1)、四边形BCDE是平行四边形．

(2)、若AB＝ $\sqrt{80}$ ，DB＝4，求四边形ABCD的面积．

查看试题解析
21. 如图，在平行四边形ABCD中，对角线AC、BD交于点O，E是BD延长线上的点，且△ACE是等边三角形．

(1)、求证：四边形ABCD是菱形．

(2)、当∠EAD等于多少度时，四边形ABCD是正方形．并写出推理过程．

查看试题解析
22. 某个体户购进一批时令水果，20天销售完毕，他将本次销售情况进行了跟踪记录，根据所记录的数据绘制如下的函数图象，其中日销售量y（千克）与销售时间x（天）之间的函数关系如图（1）所示，销售单价p（元/千克）与销售时间x（天）之间的函数关系如图（2）所示．（销售额=销售单价×销售量）

(1)、直接写出y与x之间的函数解析式；

(2)、分别求第10天和第15天的销售额；

(3)、若日销售量不低于24千克的时间段为“最佳销售期”，则此次销售过程中，“最佳销售期”共有多少天?在此期间销售单价最高为多少元?

查看试题解析
23. 猜想与证明：如图①摆放矩形纸片ABCD与矩形纸片ECGF，使B，C，G三点在一条直线上，CE在边CD上．连结AF，若M为AF的中点，连结DM，ME，

(1)、试猜想DM与ME的数量关系，并证明你的结论．

(2)、拓展与延伸：
①若将“猜想与证明”中的纸片换成正方形纸片ABCD与正方形纸片ECGF，其他条件不变，则DM和ME的关系为；

②如图②摆放正方形纸片ABCD与正方形纸片ECGF，使点F在边CD上，点M仍为AF的中点，猜想并证明DM和ME的关系．下面给出部分证明过程，请把推理过程补充完整．

证明：如图③，连结AC．

∵四边形ABCD、四边形ECGF都是正方形，

∴∠DAC=∠DCA＝∠DCE＝∠CFE＝45°，

∴点E在AC上．

∴∠AEF＝∠FEC＝90°．

又∵点M是AF的中点，

∴ME＝ $\frac{1}{2}$ AF．

查看试题解析

项目	服装统一	进退场有序	动作规范	动作整齐
得分	$10$	$9$	$8$	$8$