辽宁省沈阳市皇姑区2020-2021学年八年级下学期数学期末试卷
试卷更新日期:2021-08-16 类型:期末考试
一、单选题
-
1. 下面的图形是用数学家名字命名的,其中既是轴对称图形又是中心对称图形的是( )A、
 赵爽弦图
B、
赵爽弦图
B、 笛卡尔心形线
C、
笛卡尔心形线
C、 科克曲线
D、
科克曲线
D、 斐波那契螺旋线
2. 下列各数中,不是不等式 的解的是( )A、-3 B、 C、 D、23. 下列各式从左到右的变形中,属于因式分解的是( )A、4a+4b+3=4(a+b)+3 B、(a+b)(a﹣b)=a2﹣b2 C、10a2b﹣2ab=2ab(5a﹣1) D、a2+b2=(a+b)2﹣2ab4. 下列各式与分式 相等的是( )A、 B、 C、 D、5. 如图, 中,AC<BC,如果用尺规作图的方法在BC上确定点P,使PA+PC=BC,那么符合要求的作图痕迹是( )
斐波那契螺旋线
2. 下列各数中,不是不等式 的解的是( )A、-3 B、 C、 D、23. 下列各式从左到右的变形中,属于因式分解的是( )A、4a+4b+3=4(a+b)+3 B、(a+b)(a﹣b)=a2﹣b2 C、10a2b﹣2ab=2ab(5a﹣1) D、a2+b2=(a+b)2﹣2ab4. 下列各式与分式 相等的是( )A、 B、 C、 D、5. 如图, 中,AC<BC,如果用尺规作图的方法在BC上确定点P,使PA+PC=BC,那么符合要求的作图痕迹是( ) A、
A、 B、
B、 C、
C、 D、
D、 6. 下列各式中能用平方差公式进行因式分解的是( )A、x2+x+1 B、x2+2x﹣1 C、x2﹣1 D、x2﹣2x+17. 如图,把线段AB经过平移得到线段CD,其中A,B的对应点分别为C,D.已知A(﹣1,0),B(﹣2,3),C(2,1),则点D的坐标为( )
6. 下列各式中能用平方差公式进行因式分解的是( )A、x2+x+1 B、x2+2x﹣1 C、x2﹣1 D、x2﹣2x+17. 如图,把线段AB经过平移得到线段CD,其中A,B的对应点分别为C,D.已知A(﹣1,0),B(﹣2,3),C(2,1),则点D的坐标为( )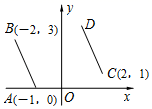 A、.(1,4) B、.(1,3) C、.(2,4) D、.(2,3)8. 如图,六边形 内部有一点 ,连结 .若 ,则 的大小为( )
A、.(1,4) B、.(1,3) C、.(2,4) D、.(2,3)8. 如图,六边形 内部有一点 ,连结 .若 ,则 的大小为( ) A、 B、 C、 D、9. 已知关于 的不等式 的解集为 ,则( )A、 B、 C、 D、10. 八年级学生去距学校10千米的博物馆参观,一部分学生骑自行车先走,过了20分钟后,其余学生乘汽车出发,结果他们同时到达,已知汽车的速度是骑车学生速度的2倍.设骑车学生的速度为x千米/小时,则所列方程正确的是( )A、 - =20 B、 - =20 C、 - = D、 =
A、 B、 C、 D、9. 已知关于 的不等式 的解集为 ,则( )A、 B、 C、 D、10. 八年级学生去距学校10千米的博物馆参观,一部分学生骑自行车先走,过了20分钟后,其余学生乘汽车出发,结果他们同时到达,已知汽车的速度是骑车学生速度的2倍.设骑车学生的速度为x千米/小时,则所列方程正确的是( )A、 - =20 B、 - =20 C、 - = D、 =二、填空题
-
11. 已知a2+a=0,则2a2+2a+2021= .12. 分解因式: .13. 如图,四边形ABCD中,AD∥BC,AD= BC,CD=BC,点E,F分别是BD,CD的中点,连接AE,EF,若BC=2,则四边形AEFD的周长为 .
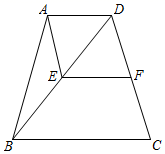 14. 如图,矩形ABCD被两条对角线分成四个小三角形,如果四个小三角形的周长的和是40厘米,矩形的周长是22厘米,则对角线AC的长为 厘米.
14. 如图,矩形ABCD被两条对角线分成四个小三角形,如果四个小三角形的周长的和是40厘米,矩形的周长是22厘米,则对角线AC的长为 厘米. 15. 如图,在等边三角形ABC中,BC边上的中线AD=5,E是AD上的一个动点,F是边AB上的一个动点,在点E,F运动的过程中,EB+EF的最小值是 .
15. 如图,在等边三角形ABC中,BC边上的中线AD=5,E是AD上的一个动点,F是边AB上的一个动点,在点E,F运动的过程中,EB+EF的最小值是 . 16. 如图,△ABC 的面积是12,点 D、E、F、G 分别是BC、AD、BE、CE 的中点,则阴影部分的面积是 .
16. 如图,△ABC 的面积是12,点 D、E、F、G 分别是BC、AD、BE、CE 的中点,则阴影部分的面积是 .
三、解答题
-
17. 解不等式组: .18. 化简并求值: ,其中﹣1≤x≤2,且x为整数.19. 如图,在网格中建立平面直直角坐标系,每个小正方形边长都是1,其顶点叫做格点,△ABC的顶点都在格点上,A,B,C三点的坐标分别为(﹣1,0),(0,3),(﹣2,2).
 (1)、将△ABC绕原点O顺时针旋转90°得到△A1B1C1 , 画出△A1B1C1;(不写作法,其中点A、B、C的对应点分别为A1、B1、C1)(2)、以点O为对称中心,画出△ABC的中心对称图形△A2B2C2;(不写作法,其中点A、B、C的对应点分别为A2、B2、C2)(3)、直接填空:连接C1A2和C2B1后得四边形C1A2C2B1的面积为(面积单位).20. 如图,△ABC中,AB=AC,∠ABC的平分线交AC于D,AE∥BC交BD的延长线于点E,AF⊥AB交BE于点F.
(1)、将△ABC绕原点O顺时针旋转90°得到△A1B1C1 , 画出△A1B1C1;(不写作法,其中点A、B、C的对应点分别为A1、B1、C1)(2)、以点O为对称中心,画出△ABC的中心对称图形△A2B2C2;(不写作法,其中点A、B、C的对应点分别为A2、B2、C2)(3)、直接填空:连接C1A2和C2B1后得四边形C1A2C2B1的面积为(面积单位).20. 如图,△ABC中,AB=AC,∠ABC的平分线交AC于D,AE∥BC交BD的延长线于点E,AF⊥AB交BE于点F. (1)、若∠BAC=40°,求∠AFE的度数;(2)、若AD=DC=2,则AF的长为(直接填空).21. 某超市用4000元购进某种服装销售,由于销售状况良好,超市又调拨9000元资金购进该种服装,但这次的进价比第一次的进价降低了20%,购进的数量是第一次的2倍还多25件,问这种服装的第一次进价是每件多少元?22. 已知:如图,BD垂直平分AC,∠BCD=∠ADE,AE⊥AC.
(1)、若∠BAC=40°,求∠AFE的度数;(2)、若AD=DC=2,则AF的长为(直接填空).21. 某超市用4000元购进某种服装销售,由于销售状况良好,超市又调拨9000元资金购进该种服装,但这次的进价比第一次的进价降低了20%,购进的数量是第一次的2倍还多25件,问这种服装的第一次进价是每件多少元?22. 已知:如图,BD垂直平分AC,∠BCD=∠ADE,AE⊥AC. (1)、求证:四边形ABDE是平行四边形;(2)、若AE=DE=3,AD=4,则AC的长为(直接填空).23. 现有甲、乙两家果园的草莓可供采摘,这两家草莓的品质相同,定价均为每千克30元,但两家果园的采摘方案不同:
(1)、求证:四边形ABDE是平行四边形;(2)、若AE=DE=3,AD=4,则AC的长为(直接填空).23. 现有甲、乙两家果园的草莓可供采摘,这两家草莓的品质相同,定价均为每千克30元,但两家果园的采摘方案不同:甲果园:需购买36元门票,采摘的草莓按定价6折优惠;
乙果园:不需要购买门票,采摘的草林按定价付款不优惠.
设小明采摘的草莓数量为x千克,他在甲、乙果园采摘所需总费用分别为y甲、y乙元.
(1)、分别求出y甲、y乙与x之间的函数关系式;(2)、小明应选择哪家果园采摘草莓更合算?24. 如图,在平面直角坐标系中,直线y= x+2与y轴、x轴分别交于点A,B,点M在线段AB上运动(不与点A,B重合),连接OM. (1)、求线段OB的长;(2)、设点M的横坐标为m,△BOM的面积为S,求S关于m的函数关系式(不必写出自变量m的取值范围);(3)、若点M为线段AB的中点,点P为射线BO上的动点,将△APM沿直线PM折叠得到△A1PM,若以点A1、B、P、M为顶点的四边形是平行四边形,直接写出点A1的横坐标.25. 已知正方形ABCD,∠EAF=45°,将∠EAF绕顶点A旋转,角的两边始终与直线CD交于点E,与直线BC交于点F,连接EF.
(1)、求线段OB的长;(2)、设点M的横坐标为m,△BOM的面积为S,求S关于m的函数关系式(不必写出自变量m的取值范围);(3)、若点M为线段AB的中点,点P为射线BO上的动点,将△APM沿直线PM折叠得到△A1PM,若以点A1、B、P、M为顶点的四边形是平行四边形,直接写出点A1的横坐标.25. 已知正方形ABCD,∠EAF=45°,将∠EAF绕顶点A旋转,角的两边始终与直线CD交于点E,与直线BC交于点F,连接EF. (1)、如图①,当BF=DE时,求证:△ABF≌△ADE;(2)、若∠EAF旋转到如图②的位置时,求证:∠AFB=∠AFE;(3)、若BC=4,当边AE经过线段BC的中点时,在AF的右侧作以AF为腰的等腰直角三角形AFP,直接写出点P到直线AB的距离.
(1)、如图①,当BF=DE时,求证:△ABF≌△ADE;(2)、若∠EAF旋转到如图②的位置时,求证:∠AFB=∠AFE;(3)、若BC=4,当边AE经过线段BC的中点时,在AF的右侧作以AF为腰的等腰直角三角形AFP,直接写出点P到直线AB的距离.