辽宁省沈阳市郊联体2020-2021学年高二下学期数学期末考试试卷
试卷更新日期:2021-08-16 类型:期末考试
一、单选题
-
1. 已知集合 ,则 ( )A、 B、 C、 D、2. 设 为实数,且 ,则下列不等式正确的是( )A、 B、 C、 D、3. 函数 的定义域是( )A、 B、 C、 D、4. 若正数x,y满足 ,当 取得最小值时, 的值为( )A、2 B、3 C、4 D、55. 函数 的图象大致为( )A、
 B、
B、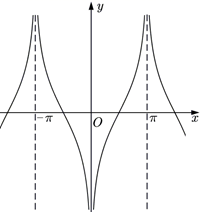 C、
C、 D、
D、 6. 国家速滑馆又称“冰丝带”,是北京2020年冬奥会的标志性场馆,拥有亚洲最大的全冰面设计,但整个系统的碳排放接近于零,做到真正的智慧场馆、绿色场馆.并且为了倡导绿色可循环的理念,场馆还配备了先进的污水、雨水过滤系统.已知过滤过程中废水的污染物数量 与时间 的关系为 ( 为最初污染物数量).如果前4小时消除了20%的污染物,那么污染物消除至最初的64%还需要( )小时.
6. 国家速滑馆又称“冰丝带”,是北京2020年冬奥会的标志性场馆,拥有亚洲最大的全冰面设计,但整个系统的碳排放接近于零,做到真正的智慧场馆、绿色场馆.并且为了倡导绿色可循环的理念,场馆还配备了先进的污水、雨水过滤系统.已知过滤过程中废水的污染物数量 与时间 的关系为 ( 为最初污染物数量).如果前4小时消除了20%的污染物,那么污染物消除至最初的64%还需要( )小时. A、3.6 B、3.8 C、4 D、4.27. 已知命题 在 内单调递增,命题 ,则p是q的( )A、充要条件 B、充分不必要条件 C、必要不充分条件 D、既不充分也不必要条件8. 已知函数 ,以下结论正确的是( )A、函数 在区间 上是减函数 B、 C、若方程 恰有5个不相等的实根,则 D、若函数 在区间 上有8个零点 ,则
A、3.6 B、3.8 C、4 D、4.27. 已知命题 在 内单调递增,命题 ,则p是q的( )A、充要条件 B、充分不必要条件 C、必要不充分条件 D、既不充分也不必要条件8. 已知函数 ,以下结论正确的是( )A、函数 在区间 上是减函数 B、 C、若方程 恰有5个不相等的实根,则 D、若函数 在区间 上有8个零点 ,则二、多选题
-
9. 已知函数 ,则下列说法正确的是( )A、若函数 的定义域为 ,则实数m的取值范围是 B、若函数 的值域为 ,则实数 C、若函数 在区间 上为增函数,则实数m的取值范围是 D、若 ,则不等式 的解集为10. 我国古代数学名著《九章算术》中记载有“耗子穿墙”问题:今有垣厚五尺两鼠对穿大鼠日一尺,小鼠亦日一尺,大鼠日自倍,小鼠日自半.下列说法中正确的有( )A、大鼠与小鼠在第三天相逢 B、大鼠与小鼠在第四天相逢 C、大鼠一共穿墙 尺 D、大鼠和小鼠穿墙的长度比为11. 已知e为自然对数的底数,则下列判断正确的是( )A、3e﹣2π<3πe﹣2 B、πlog3e>3logπe C、logπe D、πe<eπ12. 已知函数 ,若关于 的方程 有5个不同的实根,则实数 可能的取值有( )A、 B、 C、 D、
三、填空题
-
13. 幂函数 在区间 上是减函数,则 .14. 已知函数 与 的图象有且只有一个公共点,求k的取值范围 .15. 已知定义在R上的偶函数 在 上单调递增,实数a满足 ,则实数a的取值范围是.16. 已知实数 ,函数 ,若对任意 ,总存在 ,使得 ,则a的最大值为.
四、解答题
-
17. 设p:实数x满足x2-4ax+3a2<0,a∈R;q:实数x满足x2-x-6≤0或x2+2x-8>0.若a<0且p是q的充分不必要条件,求实数a的取值范围.18. 已知定义域为 的函数 是奇函数.(1)、求 的值;(2)、判断 在 上的单调性,并用定义证明;(3)、解不等式 .19. 某市2019年引进天然气作为能源,并将该项目工程承包给中昱公司.已知中昱公司为该市铺设天然气管道的固定成本为35万元,每年的管道维修费用为5万元.此外,该市若开通 千户使用天然气用户 ,公司每年还需投入成本 万元,且 .通过市场调研,公司决定从每户天然气新用户征收开户费用2500元,且用户开通天然气后,公司每年平均从每户使用天然气的过程中获利360元.(1)、设该市2019年共发展使用天然气用户 千户,求中昱公司这一年利润 (万元)关于 的函数关系式;(2)、在(1)的条件下,当 等于多少 最大?且 最大值为多少?20. 在① ,② ,③ 这三个条件中任选一个,补充下面的问题中,若问题中的 存在,求 的最小整数值;若 不存在,请说明理由.
问题:设数列 满足 ,数列 的前n项和为 .若 ▲ , 则是否存在 ,使得 ?