辽宁省大连市金普新区2020-2021学年八年级下学期数学期末试卷
试卷更新日期:2021-08-16 类型:期末考试
一、单选题
-
1. 若平行四边形中两个内角的度数比为1:2,则其中较小的内角是( )A、60° B、90° C、120° D、45°2. 直线y=2x﹣6与x轴的交点坐标是( )A、(3,0) B、(0,3) C、(0,﹣6) D、(﹣6,0)3. 甲、乙、丙、丁四人进行射击测试,每人10次射击成绩平均数均是9.2环,方差分别为S甲2=0.56,S乙2=0.60,S丙2=0.50,S丁2=0.45,则成绩最稳定的是( )A、甲 B、乙 C、丙 D、丁4. 四边形ABCD是平行四边形,下列结论中正确的是( )A、当AC⊥BD时,它是矩形 B、当AC⊥BD时,它是菱形 C、当AC=BD时,它是正方形 D、当AC⊥BD时,它是正方形5. 方程(3x﹣2)(x+1)=0的解是( )A、x B、x=﹣1 C、x1 ,x2=1 D、x1 ,x2=﹣16. 用配方法解方程x2+4x﹣5=0时,原方程应变形为( )A、(x﹣2)2=1 B、(x﹣4)2=11 C、(x+2)2=9 D、(x+4)2=217. 顺次连接菱形各边中点所得的四边形一定是( )A、梯形 B、正方形 C、菱形 D、矩形8. 若一次函数y=﹣2x﹣b图象上有两点A(﹣3,y1),B(2,y2),则下列y1 , y2大小关系正确的是( )A、y1>y2 B、y1<y2 C、y1≥y2 D、y1≤y29. 关于x的一元二次方程﹣kx2﹣6x+3=0有两个不相等的实数根,则k的取值范围是( )A、k>﹣3 B、k<3 C、k<3且k≠0 D、k>﹣3且k≠010. 如图,正方形ABCD的边长为4,点M在AB上,且AM=1,N是BD上一动点,则AN+MN的最小值为( )
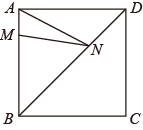 A、4 B、 C、5 D、4
A、4 B、 C、5 D、4二、填空题
-
11. 一组数据:26,28,22,x,21,它的中位数是23,则这组数据的平均数是 .12. 小张参加某企业招聘测试,笔试、面试、技能操作得分分别为91分、92分、95分,按笔试占20%、面试占40%、技能操作占40%计算成绩,则小王的成绩是分.13. 在平面直角坐标中,点A(﹣3,2)、B(﹣1,2),直线y=kx(k≠0)与线段AB有交点,则k的取值范围为 .14. 一组数据:6,7,7,7,8,则这组数据的方差是 .15. 甲、乙两人沿同一条直路走步,如果两人分别从这条道路上的 两处同时出发,都以不变的速度相向而行,图1是甲离开 处后行走的路程 (单位: )与行走时 (单位: )的函数图象,图2是甲、乙两人之间的距离(单位: )与甲行走时间x(单位: )的函数图象,则a-b= .
 16. 如图,在Rt△ABC中,∠ACB=90°,D、E、F分别是AB、BC、CA的中点,若CD=8,则EF= .
16. 如图,在Rt△ABC中,∠ACB=90°,D、E、F分别是AB、BC、CA的中点,若CD=8,则EF= .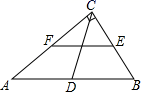
三、解答题
-
17. 已知一次函数的图象过点(2,5)与(﹣3,﹣10).(1)、求这个一次函数的解析式;(2)、直接写出这个一次函数的图象与两坐标轴的交点坐标.18. 如图,将平行四边形▱ABCD的对角线AC向两个方向延长,分别至点E和F,且使AE=CF.求证:四边形EBFD是平行四边形.
 19. 某村2018年的人均收入为30000元,2020年的人均收入为36300元.(1)、求2018年到2020年该村人均收入的年平均增长率;(2)、假设2021年该村人均收入的增长率与前两年的年平均增长率相同,请你预测2021年该村的人均收入是多少元?20. 学校组织800名学生参加义务植树活动,如表是随机抽出的50名学生义务植树的统计,根据图中的数据回答下列问题:
19. 某村2018年的人均收入为30000元,2020年的人均收入为36300元.(1)、求2018年到2020年该村人均收入的年平均增长率;(2)、假设2021年该村人均收入的增长率与前两年的年平均增长率相同,请你预测2021年该村的人均收入是多少元?20. 学校组织800名学生参加义务植树活动,如表是随机抽出的50名学生义务植树的统计,根据图中的数据回答下列问题:植树棵数
3
4
5
6
人数
6
18
16
10
(1)、植树棵数的中位数是;(2)、植树棵数的众数是;(3)、这50个人平均每人植树多少棵?(4)、估计该学校本次活动共植树棵数.21. 如图,四边形ABCD中,AB=3,BC=4,CD=12,AD=13,且∠B=90°.求四边形ABCD的面积.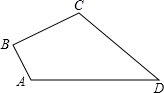 22. 如图,四边形ABCD和CEFG都是正方形,点E在BC的延长线上,且CE<BC,连接BG并延长交DE于H.
22. 如图,四边形ABCD和CEFG都是正方形,点E在BC的延长线上,且CE<BC,连接BG并延长交DE于H. (1)、写出BH与DE的位置关系,并证明;(2)、求证:∠BHC=45°.23. 甲、乙两个探测气球分别从海拔 和 处同时出发,匀速上升 .下图是甲、乙两个探测气球所在位置的海拔y(单位:m)与气球上升时间x(单位: )的函数图象.
(1)、写出BH与DE的位置关系,并证明;(2)、求证:∠BHC=45°.23. 甲、乙两个探测气球分别从海拔 和 处同时出发,匀速上升 .下图是甲、乙两个探测气球所在位置的海拔y(单位:m)与气球上升时间x(单位: )的函数图象. (1)、求这两个气球在上升过程中y关于x的函数解析式;(2)、当这两个气球的海拔高度相差 时,求上升的时间.24. 如图,矩形ABCD中,AB=6,BC=8.点P在线段CB上从点C向点B运动,点P’和点P关于AC对称,当P与B重合时运动停止,连接AP,AP’,CP’.设CP=x,四边形APCP’与矩形ABCD重合部分的面积为S.
(1)、求这两个气球在上升过程中y关于x的函数解析式;(2)、当这两个气球的海拔高度相差 时,求上升的时间.24. 如图,矩形ABCD中,AB=6,BC=8.点P在线段CB上从点C向点B运动,点P’和点P关于AC对称,当P与B重合时运动停止,连接AP,AP’,CP’.设CP=x,四边形APCP’与矩形ABCD重合部分的面积为S. (1)、填空:当P’在AD上时,x=;(2)、求S关于x的函数解析式,并写出x的取值范围.25. 如图,在平面直角坐标中,点A的坐标为(4,0),直线AB⊥x轴,直线y x+3经过点B,与y轴交于点C.
(1)、填空:当P’在AD上时,x=;(2)、求S关于x的函数解析式,并写出x的取值范围.25. 如图,在平面直角坐标中,点A的坐标为(4,0),直线AB⊥x轴,直线y x+3经过点B,与y轴交于点C. (1)、填空:点B的坐标为;(2)、直线l经过点C,与直线AB交于点D,E是直线AB上一点,且∠ECD=∠OCD,CE=5,求直线l的解析式;(3)、在(2)的条件下,点P在直线l上运动,点Q在直线OE上运动,若以P、Q、B、C为顶点的四边形为平行四边形,直接写出点P的坐标.26. 如图1,在正方形ABCD中,点E在边BC上,点F在CD的延长线上,DF=BE.
(1)、填空:点B的坐标为;(2)、直线l经过点C,与直线AB交于点D,E是直线AB上一点,且∠ECD=∠OCD,CE=5,求直线l的解析式;(3)、在(2)的条件下,点P在直线l上运动,点Q在直线OE上运动,若以P、Q、B、C为顶点的四边形为平行四边形,直接写出点P的坐标.26. 如图1,在正方形ABCD中,点E在边BC上,点F在CD的延长线上,DF=BE. (1)、求证:△AEF是等腰直角三角形;(2)、如图2,过点A作AH⊥EF垂足为H,交CD于点G,连接BH.
(1)、求证:△AEF是等腰直角三角形;(2)、如图2,过点A作AH⊥EF垂足为H,交CD于点G,连接BH.①求证:BE AB;
②图2中,若CE=4,DG=3,求BE的长.