吉林省长春市宽城区2020-2021学年八年级下学期数学期末试卷
试卷更新日期:2021-08-16 类型:期末考试
一、单选题
-
1. 要使根式 有意义,则x的取值范围是( )A、x>1 B、x≥1 C、x<1 D、x≤12. 在平面直角坐标系中,点P(3,-4)到x轴的距离是( )A、3 B、-3 C、4 D、-43. 下列各点中,在反比例函数 图象上的是A、(-1,8) B、(-2,4) C、(1,7) D、(2,4)4. 某校评选先进班集体,从“学习”、“卫生”、“纪律”、“活动参与”四个方面考核打分,各项满分均为 ,所占比例如下表:
项目
学习
卫生
纪律
活动参与
所占比例
八年级 班这四项得分依次为 , , , ,则该班四项综合得分(满分 )为( )
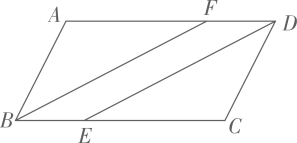
A、 B、 C、 D、5. 如图,在△ABC中,∠A=40°,AB=AC,点D在AC边上,以CB,CD为边作▱BCDE,则∠E的度数为( ) A、40° B、50° C、60° D、70°6. 如图, 是 的中线,四边形 是平行四边形,增加下列条件,能判断 是菱形的是( )
A、40° B、50° C、60° D、70°6. 如图, 是 的中线,四边形 是平行四边形,增加下列条件,能判断 是菱形的是( ) A、 B、 C、 D、7. 用四块大正方形地砖和一块小正方形地砖拼成如图所示的实线图案,每块大正方形地砖的面积为a,小正方形地砖的面积为b,依次连接四块大正方形地砖的中心得到正方形ABCD.则正方形ABCD的面积为( )
A、 B、 C、 D、7. 用四块大正方形地砖和一块小正方形地砖拼成如图所示的实线图案,每块大正方形地砖的面积为a,小正方形地砖的面积为b,依次连接四块大正方形地砖的中心得到正方形ABCD.则正方形ABCD的面积为( )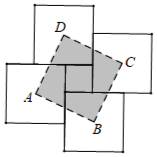 A、a+b B、a-b C、2a+b D、2a-b8. 如图,矩形 的顶点 在反比例函数 的图象上,点 和点 在 边上, ,连接 轴,则 的值为( )
A、a+b B、a-b C、2a+b D、2a-b8. 如图,矩形 的顶点 在反比例函数 的图象上,点 和点 在 边上, ,连接 轴,则 的值为( )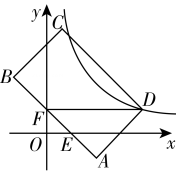 A、 B、3 C、4 D、
A、 B、3 C、4 D、二、填空题
-
9. 计算: .10. 若一次函数 的图像与 轴交于点 ,则 .11. 如图,在平行四边形ABCD中,点E是CD的中点,AE、BC的延长线交于点F.若△ECF的面积为1,则平行四边形ABCD的面积为 .
 12. 如图,在平面直角坐标系中,点P是正比例函数y=x图象上的一点,点A的坐标为(0,1),点B的坐标为(4,1),当PB+PA取最小值时,点P的坐标为 .
12. 如图,在平面直角坐标系中,点P是正比例函数y=x图象上的一点,点A的坐标为(0,1),点B的坐标为(4,1),当PB+PA取最小值时,点P的坐标为 . 13. 如图, , 是正方形 的对角线 上的两点, , ,则四边形 的周长是 .
13. 如图, , 是正方形 的对角线 上的两点, , ,则四边形 的周长是 .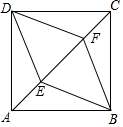 14. 点P,Q,R在反比例函数 (常数k>0,x>0)图象上的位置如图所示,分别过这三个点作x轴、y轴的平行线.图中所构成的阴影部分面积从左到右依次为S1 , S2 , S3.若OE=ED=DC,S1+S3=27,则S2的值为.
14. 点P,Q,R在反比例函数 (常数k>0,x>0)图象上的位置如图所示,分别过这三个点作x轴、y轴的平行线.图中所构成的阴影部分面积从左到右依次为S1 , S2 , S3.若OE=ED=DC,S1+S3=27,则S2的值为.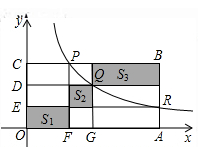
三、解答题
-
15. 计算: .16. 如图,点E,F在 的边 , 上, , ,连接 , .求证:四边形 是平行四边形.
 17. 如图,在平面直角坐标系中,一次函数 的图象与函数 (m >0,x>0)的图象交于A(3,a)、B(14-2a,2)两点.
17. 如图,在平面直角坐标系中,一次函数 的图象与函数 (m >0,x>0)的图象交于A(3,a)、B(14-2a,2)两点.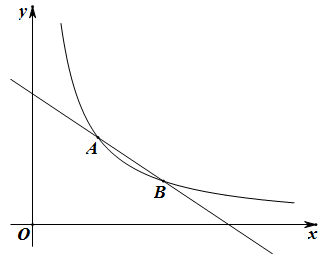 (1)、求m的值.(2)、求一次函数 所对应的函数表达式.18. 图①、图②、图③均是5×5的正方形网格,每个小正方形的顶点称为格点,每个小正方形的边长均为1,点A、B均在格点上.只用无刻度的直尺,在给定的网格中按下列要求画图,所画图形的顶点均在格点上且不全等,不要求写画法.
(1)、求m的值.(2)、求一次函数 所对应的函数表达式.18. 图①、图②、图③均是5×5的正方形网格,每个小正方形的顶点称为格点,每个小正方形的边长均为1,点A、B均在格点上.只用无刻度的直尺,在给定的网格中按下列要求画图,所画图形的顶点均在格点上且不全等,不要求写画法.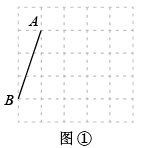 (1)、在图①中以线段AB为边画一个平行四边形.(2)、在图②中以线段AB为边画一个正方形.
(1)、在图①中以线段AB为边画一个平行四边形.(2)、在图②中以线段AB为边画一个正方形. (3)、在图③中以线段AB为边画一个菱形,所画菱形的面积为 .
(3)、在图③中以线段AB为边画一个菱形,所画菱形的面积为 . 19. 如图,在△ABC中,AB=AC , 点D、E分别是线段BC、AD的中点,过点A作BC的平行线交BE的延长线于点F , 连接CF .
19. 如图,在△ABC中,AB=AC , 点D、E分别是线段BC、AD的中点,过点A作BC的平行线交BE的延长线于点F , 连接CF .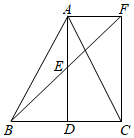 (1)、求证:△BDE≌△FAE;(2)、求证:四边形ADCF为矩形.20. 某校拟派一名跳高运动员参加校际比赛,对甲、乙两名同学进行了8次跳高选拔比赛,他们的原始成绩(单位:cm)如下表:
(1)、求证:△BDE≌△FAE;(2)、求证:四边形ADCF为矩形.20. 某校拟派一名跳高运动员参加校际比赛,对甲、乙两名同学进行了8次跳高选拔比赛,他们的原始成绩(单位:cm)如下表:次数
成绩
学生
第1次
第2次
第3次
第4次
第5次
第6次
第7次
第8次
甲
169
165
168
169
172
173
169
167
乙
161
174
172
162
163
172
172
176
两名同学的8次跳高成绩数据分析如下表:
名称
成绩
学生
平均数
(单位:cm)
中位数
(单位:cm)
众数
(单位:cm)
方差
(单位:cm2)
甲
a
b
c
5.75
乙
169
172
172
31.25
根据图表信息回答下列问题:
(1)、求a、b、c的值.(2)、这两名同学中,的成绩更为稳定(填“甲”或“乙”).(3)、若预测跳高165cm就可能获得冠军,该校为了获取跳高比赛冠军,你认为应该选择哪位同学参赛,并说明理由21. 如图,在四边形ABCD中,AD BC,AB= AD,∠BAD的平分线交BC于点E,连结DE.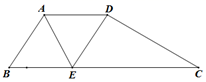 (1)、求证:四边形ABED是菱形.(2)、连结BD.若CE=2BE,AE=4,BD=6,则△CDE的面积是 .22. 已知A、B两地之间有一条公路.甲车从A地出发匀速开往B地,甲车出发2小时后,乙车从B地出发匀速开往A地,甲车出发6小时,两车同时到达各自的目的地.两车行驶的路程之和y(千米)与甲车行驶的时间x(时)之间的函数关系如图所示.
(1)、求证:四边形ABED是菱形.(2)、连结BD.若CE=2BE,AE=4,BD=6,则△CDE的面积是 .22. 已知A、B两地之间有一条公路.甲车从A地出发匀速开往B地,甲车出发2小时后,乙车从B地出发匀速开往A地,甲车出发6小时,两车同时到达各自的目的地.两车行驶的路程之和y(千米)与甲车行驶的时间x(时)之间的函数关系如图所示.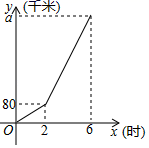 (1)、甲车的速度为千米/时,a的值为 .(2)、求乙车出发后,y与x之间的函数关系式.(3)、当甲、乙两车相距100千米时,求甲车行驶的时间.23. (教材呈现)下图是华师版八年级下册数学教材第121页的部分内容.
(1)、甲车的速度为千米/时,a的值为 .(2)、求乙车出发后,y与x之间的函数关系式.(3)、当甲、乙两车相距100千米时,求甲车行驶的时间.23. (教材呈现)下图是华师版八年级下册数学教材第121页的部分内容. (1)、(问题解决)如图①,已知矩形纸片 ,将矩形纸片沿过点 的直线折叠,使点 落在边 上,点 的对应点为 ,折痕为 ,点 在 上.求证:四边形 是正方形.(2)、(规律探索)由(问题解决)可知,图①中的 为等腰三角形.现将图①中的点 沿 向右平移至点 处(点 在点 的左侧),如图②,折痕为 ,点 在 上,点 在 上,那么 还是等腰三角形吗?请说明理由.(3)、(结论应用)在图②中,当 时,将矩形纸片继续折叠如图③,使点 与点 重合,折痕为 ,点 在 上.要使四边形 为菱形,则 .24.(1)、模型建立:如图①,在Rt△ABC中,∠ACB=90°,AC=BC.直线ED经过点C,过点A作AD⊥ED于D,过点B作BE⊥ED于E.求证:△BEC≌△CDA.
(1)、(问题解决)如图①,已知矩形纸片 ,将矩形纸片沿过点 的直线折叠,使点 落在边 上,点 的对应点为 ,折痕为 ,点 在 上.求证:四边形 是正方形.(2)、(规律探索)由(问题解决)可知,图①中的 为等腰三角形.现将图①中的点 沿 向右平移至点 处(点 在点 的左侧),如图②,折痕为 ,点 在 上,点 在 上,那么 还是等腰三角形吗?请说明理由.(3)、(结论应用)在图②中,当 时,将矩形纸片继续折叠如图③,使点 与点 重合,折痕为 ,点 在 上.要使四边形 为菱形,则 .24.(1)、模型建立:如图①,在Rt△ABC中,∠ACB=90°,AC=BC.直线ED经过点C,过点A作AD⊥ED于D,过点B作BE⊥ED于E.求证:△BEC≌△CDA.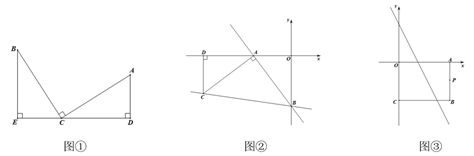 (2)、模型应用:
(2)、模型应用:如图②,在平面直角坐标系中,直线l1: 交x轴于点A,交y轴于点B,将直线l1绕着点B逆时针旋转45°至l2 . 过点A作AC⊥l1交l2于点C,过点C作CD⊥x轴于点D.求直线l2所对应的函数表达式.
(3)、如图③,在矩形ABCO中,O为坐标原点,点B的坐标为(8,-6),A、C两点分别在x轴、y轴上.P是线段AB上的动点,点D在第四象限,且是直线y=-2x+6上的一点.若△PCD是不以点C为直角顶点的等腰直角三角形,直接写出点D的横坐标.