吉林省白城市大安市2020-2021学年八年级下学期数学期末试卷
试卷更新日期:2021-08-16 类型:期末考试
一、单选题
-
1. 下列计算正确的是( )A、 B、 C、 D、2. 下列命题是真命题的是( )A、对角线互相平分的四边形是平行四边形 B、对角线相等的四边形是矩形 C、对角线互相垂直的四边形是菱形 D、对角线互相垂直的四边形是正方形3. 下列各组数中能作为直角三角形的三边长是( )A、7,24,25 B、 ,2, C、2,5,6 D、13,14,154. 某校男子足球队22名队员的年龄如下表所示:
年龄/岁
14
15
16
17
18
19
人数
2
1
3
6
7
3
这些队员年龄的众数和中位数分别是( )
A、18,17 B、17,18 C、18,17.5 D、17.5,185. 一次函数y = 2x - 1图象经过( )象限A、一、二、三 B、一、二、四 C、二、三、四 D、一、三、四6. 如图,函数 经过点 ,则关于x的不等式 的解集为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
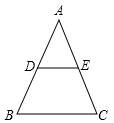
7. 计算: = .8. 函数 的自变量x的取值范围是 .9. 直线y = 3x - 2向下平移2个单位长度得到的直线是 .10. 甲、乙两名射击手的50次测试的平均成绩都是8环,方差分别是S甲2=0.4,S乙2=1.2,则成绩比较稳定的是 (填“甲”或“乙”)11. 如图所示,DE是△ABC的中位线,BC=8,则DE= .
 12. 如图,在菱形ABCD中,对角线AC与BD相交于点O,AC=8,BD=6,OE⊥BC,垂足为点E,则OE= .
12. 如图,在菱形ABCD中,对角线AC与BD相交于点O,AC=8,BD=6,OE⊥BC,垂足为点E,则OE= . 13. 如图,在平面直角坐标系中,A(4,0),B(0,3),以点A为圆心,AB长为半径画弧,交x轴的负半轴于点C,则点C坐标为 .
13. 如图,在平面直角坐标系中,A(4,0),B(0,3),以点A为圆心,AB长为半径画弧,交x轴的负半轴于点C,则点C坐标为 . 14. 在平面坐标系中,已知点A(2,3),B(5,8),直线y=kx-k(k≠0)与线段AB有交点,则k的取值范围为 .
14. 在平面坐标系中,已知点A(2,3),B(5,8),直线y=kx-k(k≠0)与线段AB有交点,则k的取值范围为 .三、解答题
-
15. 计算16. “中华人民共和国道路交通管理条例”规定:小汽车在城街路上行驶速度不得超过 km/h.如图,一辆小汽车在一条城市街路上直道行驶,某一时刻刚好行驶到路对面车速检测仪正前方 m处,过了2s后,测得小汽车与车速检测仪间距离为 m,这辆小汽车超速了吗?
 17. 如图,点E、F分别在菱形 的边 , 上,且 .
17. 如图,点E、F分别在菱形 的边 , 上,且 .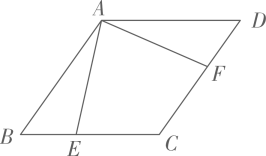
求证: .
18. 已知一次函数y=kx+b的图象经过点(-2,6),且与直线y=2x平行,求该一次函数的解析式.19. 如图,在4×4的正方形网格中,每个小格的顶点叫做格点,以格点为顶点按下列要求画图.
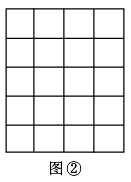 (1)、在图①中画一条线段AB,使AB= ,线段AB的端点在格点上;(2)、在图②中画一个斜边长为 的等腰直角三角形DCE,其中∠DCE=90°,三角形的顶点在格点上.20. 如图,正方形ABCD , 点E , F分别在AD , CD上,且DE=CF , AF与BE相交于点G .
(1)、在图①中画一条线段AB,使AB= ,线段AB的端点在格点上;(2)、在图②中画一个斜边长为 的等腰直角三角形DCE,其中∠DCE=90°,三角形的顶点在格点上.20. 如图,正方形ABCD , 点E , F分别在AD , CD上,且DE=CF , AF与BE相交于点G .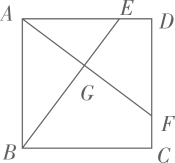 (1)、求证:BE=AF;(2)、若AB=4,DE=1,求AG的长.21. 如图,直线y=x+2与x轴、y轴分别相交于A、B两点,以OB为边在y轴右侧作等边三角形OBC.
(1)、求证:BE=AF;(2)、若AB=4,DE=1,求AG的长.21. 如图,直线y=x+2与x轴、y轴分别相交于A、B两点,以OB为边在y轴右侧作等边三角形OBC.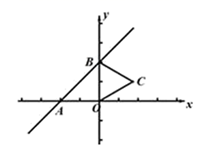 (1)、求点C的坐标;(2)、将点C向左平移m个单位,使其对应点D恰好落在直线AB上,求m的值.22. 小手拉大手,共创文明城.某校为了了解家长对南宁市创建全国文明城市相关知识的知晓情况,通过发放问卷进行测评,从中随机抽取 份答卷,并统计成绩(成绩得分用 表示,单位:分),收集数据如下:
(1)、求点C的坐标;(2)、将点C向左平移m个单位,使其对应点D恰好落在直线AB上,求m的值.22. 小手拉大手,共创文明城.某校为了了解家长对南宁市创建全国文明城市相关知识的知晓情况,通过发放问卷进行测评,从中随机抽取 份答卷,并统计成绩(成绩得分用 表示,单位:分),收集数据如下:整理数据:
分析数据:
平均分
中位数
众数
根据以上信息,解答下列问题:
(1)、直接写出上述表格中 的值;(2)、该校有 名家长参加了此次问卷测评活动,请估计成绩不低于 分的人数是多少?(3)、请从中位数和众数中选择一个量, 结合本题解释它的意义.23. 甲乙两地相距300千米,一辆货车和一辆轿车先后从甲地出发向乙地,轿车比货车晚出发1.5小时,如图,线段OA表示货车离甲地的距离y(千米)与时间x(小时)之间的函数关系;折线BCD表示轿车离甲地的距离y(千米)与时间x(小时)之间的函数关系.请根据图象解答下列问题: (1)、货车的速度是 km/h,B点坐标为;(2)、在轿车行驶过程中,轿车行驶多长时间两车相遇?(3)、直接写出:在行驶过程中,货车行驶多长时间,两车相距15千米?24. A城有肥料400吨,B城有肥料300吨,现要把这些肥料全部运往C、D两乡镇,从A城运往C、D两乡镇肥料费为20元/吨和25元/吨;从B城往C、D两乡镇运肥料的费用分别为15元/吨和24元/吨,C乡镇需要肥料340吨,D乡镇需要肥料360吨.设A城运往C乡镇x吨肥料,请解答下列问题:(1)、根据题意,填写下列表格:
(1)、货车的速度是 km/h,B点坐标为;(2)、在轿车行驶过程中,轿车行驶多长时间两车相遇?(3)、直接写出:在行驶过程中,货车行驶多长时间,两车相距15千米?24. A城有肥料400吨,B城有肥料300吨,现要把这些肥料全部运往C、D两乡镇,从A城运往C、D两乡镇肥料费为20元/吨和25元/吨;从B城往C、D两乡镇运肥料的费用分别为15元/吨和24元/吨,C乡镇需要肥料340吨,D乡镇需要肥料360吨.设A城运往C乡镇x吨肥料,请解答下列问题:(1)、根据题意,填写下列表格:城、乡/吨数
C
D
A
x
B
(2)、设总运费为W(元),求出W(元)与x(吨)的函数关系式,并写出自变量的取值范围;(3)、求怎样调运可使总运费最少?最少为多少元?25. (感知)如图①,点M是正方形ABCD的边BC上一点,点N是CD延长线上一点,且MA⊥AN,易证△ABM≌△ADN,进而证得BM=DN(不要求证明) (1)、(应用)如图②,在正方形ABCD中,点E、F分别在边BC、CD上,且∠EAF=45°.求证:BE+DF=EF.(2)、(拓展)如图③,在四边形ABCD中,AB=AD,∠BAD=90°,∠ABC+∠ADC=180°,点E、F分别在边BC、CD上,且∠EAF=45°,若BD=3.5,EF=2,则四边形BEFD的周长为 .26. 已知,如图,正方形ABCD的边长为4厘米,点P从点A出发,经A→B→C沿正方形的边以2厘米/秒的速度运动;点Q在CD上,CQ=1.设运动时间为t秒,△APQ的面积为S平方厘米.
(1)、(应用)如图②,在正方形ABCD中,点E、F分别在边BC、CD上,且∠EAF=45°.求证:BE+DF=EF.(2)、(拓展)如图③,在四边形ABCD中,AB=AD,∠BAD=90°,∠ABC+∠ADC=180°,点E、F分别在边BC、CD上,且∠EAF=45°,若BD=3.5,EF=2,则四边形BEFD的周长为 .26. 已知,如图,正方形ABCD的边长为4厘米,点P从点A出发,经A→B→C沿正方形的边以2厘米/秒的速度运动;点Q在CD上,CQ=1.设运动时间为t秒,△APQ的面积为S平方厘米.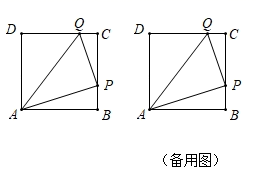 (1)、当t=2时,△APQ的面积为 平方厘米;(2)、求BP的长(用含t的代数式表示);(3)、当点P在线段BC上运动,且△APQ为等腰三角形时,求此时t的值;(4)、求S与t的函数关系式.
(1)、当t=2时,△APQ的面积为 平方厘米;(2)、求BP的长(用含t的代数式表示);(3)、当点P在线段BC上运动,且△APQ为等腰三角形时,求此时t的值;(4)、求S与t的函数关系式.