黑龙江省哈尔滨市香坊区2020-2021学年八年级下学期数学期末试卷
试卷更新日期:2021-08-16 类型:期末考试
一、单选题
-
1. 下列方程中是一元二次方程的为( )A、 B、 C、 D、2. 下列各曲线中,不表示 是 的函数的是( )A、
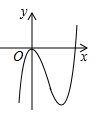 B、
B、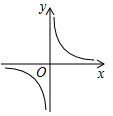 C、
C、 D、
D、 3. 下列各组数中,能作为直角三角形的三边长的是( )A、1, ,2 B、1,1, C、2,3,4 D、 ,2,4. 下列说法错误的是( )A、两组对边分别平行的四边形是平行四边形 B、一组对边平行另一组对边相等的四边形是平行四边形 C、四条边相等的四边形是菱形 D、四个角都相等的四边形是矩形5. 若关于 的一元二次方程 有两个相等的实数根,则 的值为( )A、 B、 C、 D、6. 若函数 的图象如图所示,则关于 的不等式 的解集为( )
3. 下列各组数中,能作为直角三角形的三边长的是( )A、1, ,2 B、1,1, C、2,3,4 D、 ,2,4. 下列说法错误的是( )A、两组对边分别平行的四边形是平行四边形 B、一组对边平行另一组对边相等的四边形是平行四边形 C、四条边相等的四边形是菱形 D、四个角都相等的四边形是矩形5. 若关于 的一元二次方程 有两个相等的实数根,则 的值为( )A、 B、 C、 D、6. 若函数 的图象如图所示,则关于 的不等式 的解集为( )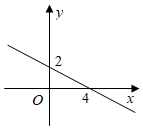 A、 B、 C、 D、7. 如图, , 分别是菱形 的边 , 的中点,且 , .则 的长为( )
A、 B、 C、 D、7. 如图, , 分别是菱形 的边 , 的中点,且 , .则 的长为( ) A、4 B、5 C、5.5 D、68. 如图,要设计一幅宽20cm,长30cm的图案,其中有两横两竖的彩条,各彩条的宽度相等,如果要使彩条所占面积是图案面积的六分之一.设彩条的宽为 cm,根据题意可列方程( )
A、4 B、5 C、5.5 D、68. 如图,要设计一幅宽20cm,长30cm的图案,其中有两横两竖的彩条,各彩条的宽度相等,如果要使彩条所占面积是图案面积的六分之一.设彩条的宽为 cm,根据题意可列方程( ) A、 B、 C、 D、9. 如图,对折一张矩形纸片 ,使 与 重合,得到折痕 ,把纸片展平,再一次折叠纸片,使点 落在 上的点 处,并使折痕经过点 ,得到折痕 交 于点 ,若纸片宽 为6,则 的长为( )
A、 B、 C、 D、9. 如图,对折一张矩形纸片 ,使 与 重合,得到折痕 ,把纸片展平,再一次折叠纸片,使点 落在 上的点 处,并使折痕经过点 ,得到折痕 交 于点 ,若纸片宽 为6,则 的长为( ) A、3 B、 C、4 D、10. 一个容器内有进水管和出水管,开始4min内只进水不出水,在随后的8min内既进水又出水,第12min后只出水不进水.进水管每分钟的进水量和出水量每分钟的出水量始终不变,容器内水量 (单位:L)与时间 (单位:min)之间的关系如图所示.
A、3 B、 C、4 D、10. 一个容器内有进水管和出水管,开始4min内只进水不出水,在随后的8min内既进水又出水,第12min后只出水不进水.进水管每分钟的进水量和出水量每分钟的出水量始终不变,容器内水量 (单位:L)与时间 (单位:min)之间的关系如图所示.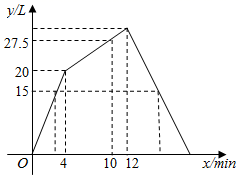
根据图象有下列说法:①进水管每分钟的进水量为5L;② 时, ;③当 时, ;④当 时, ,或 .其中正确说法的个数是( )
A、1个 B、2个 C、3个 D、4个二、填空题
-
11. 在函数 中,自变量 的取值范围是.12. 若 是方程 的一个根,则 的值为.13. 若电梯运行是匀速的,某电梯从1层(地面)直达3层用了20秒,则乘坐该电梯从2层直达8层需要的时间是秒.14. 如图,四边形ABCD是平行四边形,∠ABC=70°,BE平分∠ABC且交AD于点E,DF∥BE且交BC于点F,则∠1的度数为 .
 15. 两个相邻偶数的积是168,则这两个相邻偶数中较大的数是 .16. 若 , ,则 = .17. 如图,在 中, , 于点 , ,点 是斜边 的中点,若 ,则 的长为 .
15. 两个相邻偶数的积是168,则这两个相邻偶数中较大的数是 .16. 若 , ,则 = .17. 如图,在 中, , 于点 , ,点 是斜边 的中点,若 ,则 的长为 . 18. 如图,某货船以24海里/时的速度从A处向正东方向的D处航行,在点A处测得某岛C在北偏东60°的方向.该货船航行30分钟后到达B处,此时测得该岛在北偏东30°的方向上.则货船在航行中离小岛C的最短距离是 .
18. 如图,某货船以24海里/时的速度从A处向正东方向的D处航行,在点A处测得某岛C在北偏东60°的方向.该货船航行30分钟后到达B处,此时测得该岛在北偏东30°的方向上.则货船在航行中离小岛C的最短距离是 .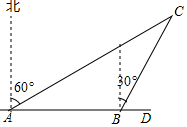 19. 如图,正方形 的边长为8, 是 边上一点,且 , 是对角线 上一动点,则 的最小值为.
19. 如图,正方形 的边长为8, 是 边上一点,且 , 是对角线 上一动点,则 的最小值为. 20. 如图, 中, 为边 上的中线,点 在 上,连接 交 于点 , , ,若 , ,则 的长为 .
20. 如图, 中, 为边 上的中线,点 在 上,连接 交 于点 , , ,若 , ,则 的长为 .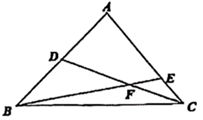
三、解答题
-
21. 解方程:(1)、(2)、22. 如图所示,在 的方格纸中,每个小正方形的边长均为1,线段 的端点 、 均在小正方形的顶点上.
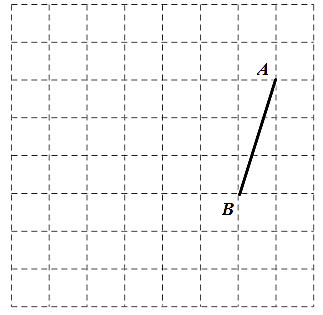 (1)、在图中画出以 为边的菱形 ,菱形的面积为8;(2)、在图中画出腰长为5的等腰三角形 ,且点 在小正方形顶点上;(3)、连接 ,请直接写出线段 的长.23. 如图,直线 的解析式为 ,直线 的解析式为 ,两条直线交于点 ,且分别与 轴交于点 、点 .
(1)、在图中画出以 为边的菱形 ,菱形的面积为8;(2)、在图中画出腰长为5的等腰三角形 ,且点 在小正方形顶点上;(3)、连接 ,请直接写出线段 的长.23. 如图,直线 的解析式为 ,直线 的解析式为 ,两条直线交于点 ,且分别与 轴交于点 、点 .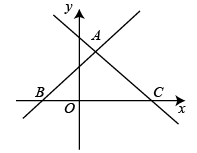 (1)、求 的面积;(2)、点 为线段 上一点,连接 ,若 ,求点 的坐标.24. 正方形 ,点 为射线 上一点,连接 ,过点 作 ,交直线 于点 ,交直线 于点 .
(1)、求 的面积;(2)、点 为线段 上一点,连接 ,若 ,求点 的坐标.24. 正方形 ,点 为射线 上一点,连接 ,过点 作 ,交直线 于点 ,交直线 于点 .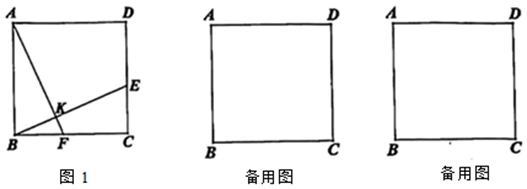 (1)、如图1,点 在边 上,求证: ;(2)、过点 作 的平行线,交直线 于点 ,交直线 于点 ,请你用等式表示线段 , , 之间的数量关系: .25. 青山村种的水稻2010年平均每公顷产7200kg,2012年平均每公顷产8712kg.(1)、求水稻每公顷产量的年平均增长率;(2)、2010年水稻平均每千克的成本为2元,每千克的售价为3元,2011年水稻平均每千克的成本比2010年的增加了10%,若2011年平均每公顷水稻的利润比2010年至少增加720元,则2011年平均每千克水稻的售价最少应为多少元?26. 已知:菱形 中,过点 作 ,垂足为点 , .
(1)、如图1,点 在边 上,求证: ;(2)、过点 作 的平行线,交直线 于点 ,交直线 于点 ,请你用等式表示线段 , , 之间的数量关系: .25. 青山村种的水稻2010年平均每公顷产7200kg,2012年平均每公顷产8712kg.(1)、求水稻每公顷产量的年平均增长率;(2)、2010年水稻平均每千克的成本为2元,每千克的售价为3元,2011年水稻平均每千克的成本比2010年的增加了10%,若2011年平均每公顷水稻的利润比2010年至少增加720元,则2011年平均每千克水稻的售价最少应为多少元?26. 已知:菱形 中,过点 作 ,垂足为点 , .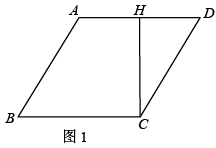
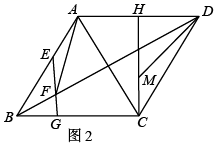
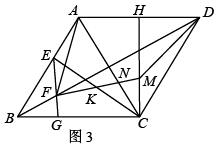 (1)、如图1,求 的度数;(2)、如图2,连接 、 ,点 在 上, 于点 ,交 于点 ,点 在 上,连接 、 , ,求证: ;(3)、如图3,在(2)的条件下,分別连接 、 , 、 交于点 , 交 于点 ,若 , ,求菱形 的面积.27. 已知:在平面直角坐标系中,直线 交 轴负半轴于点 ,交 轴于点 ,直线 的解析式为 ,经过点 的直线交 轴正半轴于点 , , .
(1)、如图1,求 的度数;(2)、如图2,连接 、 ,点 在 上, 于点 ,交 于点 ,点 在 上,连接 、 , ,求证: ;(3)、如图3,在(2)的条件下,分別连接 、 , 、 交于点 , 交 于点 ,若 , ,求菱形 的面积.27. 已知:在平面直角坐标系中,直线 交 轴负半轴于点 ,交 轴于点 ,直线 的解析式为 ,经过点 的直线交 轴正半轴于点 , , .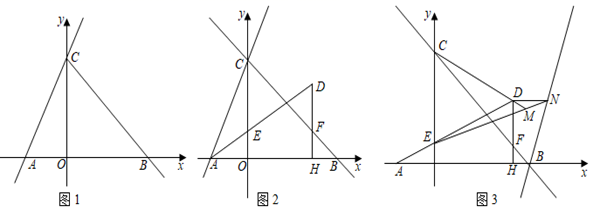 (1)、如图1,求直线 的解析式;(2)、如图2,点 在 上,过点 作 轴的垂线,交 于点 ,点 在 上,连接 并延长交直线 于点 , ,设直线 的解析式为 ,线段 的长为 ,求 与 的函数解析式;(3)、如图3,在(2)的条件下,连接 并延长至点 ,连接 , ,过点 作 轴的平行线,交 延长线于点 ,直线 解析式为 ,求点 的坐标.
(1)、如图1,求直线 的解析式;(2)、如图2,点 在 上,过点 作 轴的垂线,交 于点 ,点 在 上,连接 并延长交直线 于点 , ,设直线 的解析式为 ,线段 的长为 ,求 与 的函数解析式;(3)、如图3,在(2)的条件下,连接 并延长至点 ,连接 , ,过点 作 轴的平行线,交 延长线于点 ,直线 解析式为 ,求点 的坐标.