河北省张家口市怀安县2020-2021学年八年级下学期数学期末试卷

试卷更新日期：2021-08-16 类型：期末考试

进入出卷网下载

一、单选题

1. 下列二次根式中，无论x取什么值都有意义的是（　　）

A、 $\sqrt{x^{2} - 5}$ B、 $\sqrt{- x - 5}$ C、 $\sqrt{x}$ D、 $\sqrt{x^{2} + 1}$

查看试题解析
2. 如图，在 $△ A B C$ 中，D，E分别是 $A B$ ， $A C$ 的中点，则下列说法正确的是（）

A、 $A E = B D$ B、 $B D = D E$ C、 $∠ D E C + ∠ B = 180 °$ D、 $∠ B D E + ∠ B = 180 °$

查看试题解析
3. 如图，是一种饮料的包装盒，长、宽、高分别为 $4 c m$ 、 $3 c m$ 、 $12 c m$ ，现有一长为 $16 c m$ 的吸管插入到盒的底部，则吸管漏在盒外面的部分 $h (c m)$ 的取值范围为（）

A、 $3 < h < 4$ B、 $3 \leq h \leq 4$ C、 $2 \leq h \leq 4$ D、 $h = 4$

查看试题解析
4. 一组数据3，5，5，7，若添加一个数据5，则发生变化的统计量是（）

A、平均数 B、中位数 C、方差 D、众数

查看试题解析
5. 点P₁（x₁ ， y₁）点P₂（x₂ ， y₂）是一次函数y＝﹣4x+3图象上的两个点，且x₁＞x₂ ，则y₁与y₂的关系是（）

A、y₁＜y₂ B、y₁＞y₂ C、y₁＞y₂＞0 D、y₁＝y₂

查看试题解析
6. 三角形的三边分别为a、b、c，由下列条件不能判断它是直角三角形的是（）

A、 $a = \frac{1}{3}$ ， $b = \frac{1}{4}$ ， $c = \frac{1}{5}$ B、 $a^{2} - b^{2} = c^{2}$ C、 $a^{2} = (b + c) (b - c)$ D、 $a : b : c = 13 : 5 : 12$

查看试题解析
7. 若直线 $y = k x + b$ 经过第二、三、四象限，则直线 $y = - b x + k$ 不经过（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
8. 已知平行四边形ABCD中，∠A＋∠C＝110°，则∠B的度数为（）

A、125° B、135° C、145° D、155°

查看试题解析
9. 如图，在矩形ABCD中，对角线AC，BD交于点O，已知∠AOD=120°，AB=2，则AC的长为（）

A、2 B、4 C、6 D、8

查看试题解析
10. 将 $2020$ 个形状、大小均相同的菱形按照如图所示的方式排成一列，使得右侧菱形的顶点与左侧菱形的对角线交点重合，若这些菱形的边长均为 $a$ ，则阴影部分的周长总和等于（）

A、 $2020 a$ B、 $4038 a$ C、 $4040 a$ D、 $4042 a$

查看试题解析
11. 下列计算中，正确的是（）

A、 $\sqrt{2} + \sqrt{3} = \sqrt{5}$ B、 $2 + \sqrt{2} = 2 \sqrt{2}$ C、 $\sqrt{2} \times \sqrt{3} = \sqrt{6}$ D、 $2 \sqrt{3} - 2 = \sqrt{3}$

查看试题解析
12. 要得到函数y=2x+3的图象，只需将函数y=2x的图象（）

A、向左平移3个单位 B、向右平移3个单位 C、向下平移3个单位 D、向上平移3个单位

查看试题解析

13. 2022年将在北京-张家口举办冬季奥运会，很多学校开设了相关的课程．如表记录了某校4名同学短道速滑选拔赛成绩的平均数与方差

s^{2}

：

	队员1	队员2	队员3	队员4
平均数 $\bar{x}$ (秒)	51	50	51	50
方差 $s^{2}$ (秒²)	3.5	3.5	14.5	15.5

根据表中数据，要从中选择一名成绩好又发挥稳定的运动员参加比赛，应该选择（）

A、队员1 B、队员2 C、队员3 D、队员4

查看试题解析

14. 如图，▱ABCD中，AB=4，BC=3，∠DCB=30°，动点E从B点出发，沿B﹣C﹣D﹣A运动至A点停止，设运动的路程为x，△ABE的面积为y，则y与x的函数图象用图象表示正确的是（）

A、 B、 C、 D、

查看试题解析

二、填空题

15. 若 $\sqrt{x + 2}$ 在实数范围内有意义，则x的取值范围是．

查看试题解析
16. 已知一组数据x₁ ， x₂ ， x₃ ， x₄ ， x₅的平均数是2，那么另一组数据3x₁﹣2，3x₂﹣2，3x₃﹣2，3x₄﹣2，3x₅﹣2的平均数是．

查看试题解析
17. 如图，正方形ABCD的边长为1，点E，F分别是对角线AC上的两点，EG⊥AB．EI⊥AD，FH⊥AB，FJ⊥AD，垂足分别为G，I，H，J．则图中阴影部分的面积等于．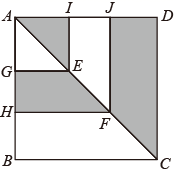

查看试题解析
18. 一次函数y₁＝kx+b与y₂＝x+a的图象如图，则下列结论：①k $<$ 0；②a $>$ 0；③关于x的方程kx﹣x＝a﹣b的解是x＝3；④当x $>$ 3时，y₁ $<$ y₂中．则正确的序号有．

查看试题解析

三、解答题

19. 计算：

(1)、 $\sqrt{27} - | - 2 \sqrt{3} | - \sqrt{3} {(2 - π)}^{0} + {(- 1)}^{2018}$ ；

(2)、 $(\sqrt{24} - \sqrt{6}) \div \sqrt{3} + \sqrt{\frac{1}{2}}$ ．

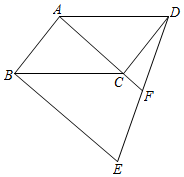
查看试题解析
20. 如图，点E在▱ABCD外，连接BE，DE，延长AC交DE于F，F为DE的中点．
求证：AF $//$ BE；

查看试题解析
21. 如图，是一个6×10的正方形网格（每个小正方形的边长均为1），点A，B，C都在格点上，请按要求完成下列各题：

(1)、过A作AD//BC（D为格点），连接BD；求证：四边形ADBC是矩形；

(2)、在图中画出AB的中点E，并求CE的长．

查看试题解析
22. 中考体育测试前，某区教育局为了了解选报引体向上的初三男生的成绩情况，随机抽测了本区部分选报引体向上项目的初三男生的成绩，并将测试得到的成绩绘成了下面两幅不完整的统计图：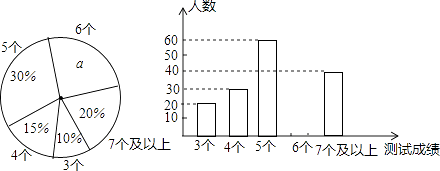
请你根据图中的信息，解答下列问题：

(1)、写出扇形图中a=%，并补全条形图；

(2)、在这次抽测中，测试成绩的众数和中位数分别是个、个．

(3)、该区体育中考选报引体向上的男生共有1800人，如果体育中考引体向上达6个以上（含6个）得满分，请你估计该区体育中考中选报引体向上的男生能获得满分的有多少名？

查看试题解析
23. 如图，一次函数y＝ax+b的图象与正比例函数y＝kx的图象交于点M ，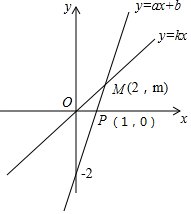

(1)、求正比例函数和一次函数的解析式；

(2)、根据图象写出使正比例函数的值大于一次函数的值的x的取值范围；

(3)、求△MOP的面积．

查看试题解析
24. 已知：甲乙两车分别从相距300千米的A、B两地同时出发相向而行，其中甲到达B地后立即返回，如图是它们离各自出发地的距离y（千米）与行驶时间x（小时）之间的函数图象．

(1)、求甲车离出发地的距离y_甲（千米）与行驶时间x（小时）之间的函数关系式，并写出自变量的取值范围；

(2)、它们出发 $\frac{9}{2}$ 小时时，离各自出发地的距离相等，求乙车离出发地的距离y_乙（千米）与行驶时间x（小时）之间的函数关系式，并写出自变量的取值范围；

(3)、在（2）的条件下，求它们在行驶的过程中相遇的时间．

查看试题解析