河北省石家庄市新乐市2020-2021学年八年级下学期数学期末试卷
试卷更新日期:2021-08-16 类型:期末考试
一、单选题
-
1. 下列调查中,不适合用抽样调查方式的是( )A、调查“神舟十一号”飞船重要零部件的产品质量 B、调查某电视剧的收视率 C、调查一批炮弹的杀伤力 D、调查一片森林的树木有多少棵2. 骆驼被称为“沙漠之舟”,它的体温随时间的变化而发生较大的变化.在这一问题中,自变量是( )A、时间 B、骆驼 C、沙漠 D、体温3. 下列各点中,在第二象限的点是A、 B、 C、 D、4. 下列图象中,y不是x的函数的是A、
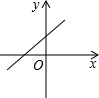 B、
B、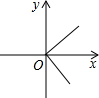 C、
C、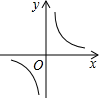 D、
D、 5. 某县三月中旬每天平均空气质量指数(AQI)分别为:118,96,60,82,56,69,86,112,108,94,为了描述这十天空气质量的变化情况,最适合用的统计图是( )A、折线统计图 B、频数分布直方图 C、条形统计图 D、扇形统计图6. 下列语句正确的是( )A、对角线互相垂直的四边形是菱形 B、有两对邻角互补的四边形为平行四边形 C、矩形的对角线相等 D、平行四边形是轴对称图形7. 如图,在矩形AOBC中,A(–2,0),B(0,1).若正比例函数y=kx的图象经过点C,则k的值为( )
5. 某县三月中旬每天平均空气质量指数(AQI)分别为:118,96,60,82,56,69,86,112,108,94,为了描述这十天空气质量的变化情况,最适合用的统计图是( )A、折线统计图 B、频数分布直方图 C、条形统计图 D、扇形统计图6. 下列语句正确的是( )A、对角线互相垂直的四边形是菱形 B、有两对邻角互补的四边形为平行四边形 C、矩形的对角线相等 D、平行四边形是轴对称图形7. 如图,在矩形AOBC中,A(–2,0),B(0,1).若正比例函数y=kx的图象经过点C,则k的值为( ) A、– B、 C、–2 D、28. 下表列出了一项实验的统计数据,表示皮球从高处自由落下时,弹跳高度b(cm)与下落时的高度d(cm)之间的关系,那么下面的式子能表示这种关系的是( )
A、– B、 C、–2 D、28. 下表列出了一项实验的统计数据,表示皮球从高处自由落下时,弹跳高度b(cm)与下落时的高度d(cm)之间的关系,那么下面的式子能表示这种关系的是( )d(cm)
50
80
100
150
b(cm)
25
40
50
75
A、b=d2 B、b=2d C、b= D、b=d+259. 如图,在▱ABCD中,AD=8,点E,F分别是BD,CD的中点,则EF等于( ) A、2 B、3 C、4 D、510. 若方程组 没有解,则一次函数y=2-x与y= -x的图像必定( )A、重合 B、平行 C、相交 D、无法确定11. 如图,四边形ABCD是菱形,A(3,0),B(0,4),则点C的坐标为( )
A、2 B、3 C、4 D、510. 若方程组 没有解,则一次函数y=2-x与y= -x的图像必定( )A、重合 B、平行 C、相交 D、无法确定11. 如图,四边形ABCD是菱形,A(3,0),B(0,4),则点C的坐标为( ) A、(-5,4). B、(-5,5). C、(-4,4). D、(-4,3)12. 某市从参加数学质量检测的4355名学生中,随机抽取了部分学生的成绩为研究对象,结果如表所示:
A、(-5,4). B、(-5,5). C、(-4,4). D、(-4,3)12. 某市从参加数学质量检测的4355名学生中,随机抽取了部分学生的成绩为研究对象,结果如表所示:分数段
0~60
60~72
72~84
84~96
96~108
108~120
人数(人)
5
8
35
42
15
百分比
20%
40%
则被抽取的学生人数是( )
A、70人 B、105人 C、175人 D、200人13. 如图,在正方形ABCD中,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,若PD+PE的最小值为5,则正方形的面积为( ) A、16 B、6.25 C、9 D、2514. 甲、乙两同学骑自行车从A地沿同一条路到B地,已知乙比甲先出发,他们离出发地的距离S(km)和骑行时间t(h)之间的函数关系如图所示,给出下列说法:①他们都骑行了20km;②乙在途中停留了0.5h;③甲、乙两人同时到达目的地;④相遇后,甲的速度小于乙的速度.根据图象信息,以上说法正确的有( )
A、16 B、6.25 C、9 D、2514. 甲、乙两同学骑自行车从A地沿同一条路到B地,已知乙比甲先出发,他们离出发地的距离S(km)和骑行时间t(h)之间的函数关系如图所示,给出下列说法:①他们都骑行了20km;②乙在途中停留了0.5h;③甲、乙两人同时到达目的地;④相遇后,甲的速度小于乙的速度.根据图象信息,以上说法正确的有( ) A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
15. 已知矩形的对角线AC与BD相交于点O,若AO=1,那么BD= .16. 已知点P在第二象限,且横坐标与纵坐标的和为1,试写出一个符合条件的点P .17. 如图,点E、F、G、H分别是任意四边形ABCD中AD、BD、BC、CA的中点,当四边形ABCD的边至少满足条件时,四边形EFGH是菱形.
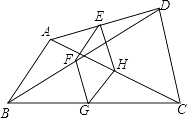 18. 无论 取何实数,直线 与 的交点不可能在第象限.19. 某物体从上午7时至下午4时的温度M(℃)是时间t(h)的函数: (其中t=0表示中午12时,t=-1表示上午11时,t=1表示13时),则上午10时此物体的温度为℃.20. 李老师开车从甲地到相距240千米的乙地,如果油箱剩余油量y(升)与行驶里程x(千米)之间是一次函数关系,其图象如图所示,那么到达乙地时油箱剩余油量是升.
18. 无论 取何实数,直线 与 的交点不可能在第象限.19. 某物体从上午7时至下午4时的温度M(℃)是时间t(h)的函数: (其中t=0表示中午12时,t=-1表示上午11时,t=1表示13时),则上午10时此物体的温度为℃.20. 李老师开车从甲地到相距240千米的乙地,如果油箱剩余油量y(升)与行驶里程x(千米)之间是一次函数关系,其图象如图所示,那么到达乙地时油箱剩余油量是升.
三、解答题
-
21. 中华文明,源远流长;中华汉字,寓意深广.为了传承优秀传统文化,某校团委组织了一次全校3000名学生参加的“汉字听写”大赛,赛后发现所有参赛学生的成绩均不低于50分.为了更好地了解本次大赛的成绩分布情况,随机抽取了其中200名学生的成绩(成绩x取整数,总分100分)作为样本进行整理,得到下列不完整的统计图表:
成绩x/分
频数
频率
50≤x<60
10
0.05
60≤x<70
20
0.10
70≤x<80
30
b
80≤x<90
a
0.30
90≤x≤100
80
0.40

请根据所给信息,解答下列问题:
(1)、a= , b=;(2)、请补全频数分布直方图;(3)、若成绩在90分以上(包括90分)的为“优”等,则该校参加这次比赛的3000名学生中成绩为“优”等的大约有多少人?22. 某科技小组制作了一个机器人,它能根据指令要求进行行进和旋转,某一指令规定:机器人先向前方行走2 m,然后左转60°,若机器人反复执行这一指令,则从出发到第一次回到原处,机器人共走了多少米?23. 下面是小林画出函数 的一部分图象,利用图象回答: (1)、自变量x的取值范围.(2)、当x取什么值时,y的最小值.最大值各是多少?(3)、在图中,当x增大时,y的值是怎样变化?24. 如图,点O是△ABC内一点,连结OB、OC,并将AB、OB、OC、AC的中点D、E、F、G依次连结,得到四边形DEFG.
(1)、自变量x的取值范围.(2)、当x取什么值时,y的最小值.最大值各是多少?(3)、在图中,当x增大时,y的值是怎样变化?24. 如图,点O是△ABC内一点,连结OB、OC,并将AB、OB、OC、AC的中点D、E、F、G依次连结,得到四边形DEFG.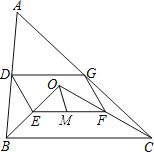 (1)、求证:四边形DEFG是平行四边形;(2)、若M为EF的中点,OM=3,∠OBC和∠OCB互余,求DG的长度.25. 某报纸上刊登了一则新闻,“某种品牌的节能灯的合格率为95%”,请据此回答下列问题:(1)、这则新闻是否说明市面上所有这种品牌的节能灯恰有5%为不合格?(2)、你认为这则消息来源于普查,还是抽样调查?为什么?(3)、如果已知在这次检查中合格产品有76个,则共有多少个节能灯接受检查?(4)、如果此次检查了两种产品,数据如下表所示,有人由此认为“A品牌的不合格率比B品牌低,更让人放心”.你同意这种说法吗?为什么?
(1)、求证:四边形DEFG是平行四边形;(2)、若M为EF的中点,OM=3,∠OBC和∠OCB互余,求DG的长度.25. 某报纸上刊登了一则新闻,“某种品牌的节能灯的合格率为95%”,请据此回答下列问题:(1)、这则新闻是否说明市面上所有这种品牌的节能灯恰有5%为不合格?(2)、你认为这则消息来源于普查,还是抽样调查?为什么?(3)、如果已知在这次检查中合格产品有76个,则共有多少个节能灯接受检查?(4)、如果此次检查了两种产品,数据如下表所示,有人由此认为“A品牌的不合格率比B品牌低,更让人放心”.你同意这种说法吗?为什么?品牌
A品牌
B品牌
被检测数
70
10
不合格数
3
1
26. 如图,P是 与弦AB所围成的图形的外部的一定点,C是 上一动点,连接PC交弦AB于点D.小腾根据学习函数的经验,对线段PC,PD,AD的长度之间的关系进行了探究.下面是小腾的探究过程,请补充完整:
(1)、对于点C在 上的不同位置,画图、测量,得到了线段PC,PD,AD的长度的几组值,如下表:位置1
位置2
位置3
位置4
位置5
位置6
位置7
位置8
PC/cm
3.44
3.30
3.07
2.70
2.25
2.25
2.64
2.83
PD/cm
3.44
2.69
2.00
1.36
0.96
1.13
2.00
2.83
AD/cm
0.00
0.78
1.54
2.30
3.01
4.00
5.11
6.00
在PC,PD,AD的长度这三个量中,确定的长度是自变量,的长度和的长度都是这个自变量的函数;
(2)、在同一平面直角坐标系xOy中,画出(1)中所确定的函数的图象; (3)、结合函数图象,解决问题:当PC=2PD时,AD的长度约为 cm.
(3)、结合函数图象,解决问题:当PC=2PD时,AD的长度约为 cm. 27. 如图,在平面直角坐标系中,A(4,0),B(0,2),C(4,4).已知四边形ABCD为菱形,其中AB与BC为一组邻边.
27. 如图,在平面直角坐标系中,A(4,0),B(0,2),C(4,4).已知四边形ABCD为菱形,其中AB与BC为一组邻边. (1)、请在图中作出菱形ABCD,并求出菱形ABCD的面积;(2)、过点A的直线l:y= x+b与线段CD相交于点E,请在图中作出直线l的图象,并求出△ADE的面积.
(1)、请在图中作出菱形ABCD,并求出菱形ABCD的面积;(2)、过点A的直线l:y= x+b与线段CD相交于点E,请在图中作出直线l的图象,并求出△ADE的面积.