河北省石家庄市栾城区2020-2021学年八年级下学期数学期末试卷
试卷更新日期:2021-08-16 类型:期末考试
一、单选题
-
1. 如图,五角星盖住的点的坐标可能为( )
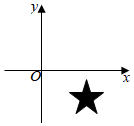 A、(3,2) B、(﹣3,2) C、(﹣3,﹣2) D、(3,﹣2)2. 下列判断错误的是( )A、四个角相等的四边形是矩形 B、对角线垂直的四边形是菱形 C、对角线相等的平行四边形是矩形 D、对角线垂直的平行四边形是菱形3. 如图,平行四边形ABCD的周长为36,对角线AC、BD相交于点O, 点E是CD的中点,BD=12,则△DOE的周长为( )
A、(3,2) B、(﹣3,2) C、(﹣3,﹣2) D、(3,﹣2)2. 下列判断错误的是( )A、四个角相等的四边形是矩形 B、对角线垂直的四边形是菱形 C、对角线相等的平行四边形是矩形 D、对角线垂直的平行四边形是菱形3. 如图,平行四边形ABCD的周长为36,对角线AC、BD相交于点O, 点E是CD的中点,BD=12,则△DOE的周长为( )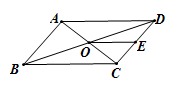 A、12 B、15 C、18 D、214. 在平面直角坐标系中,函数 的图象经过( )A、一、二、三象限 B、一、二、四象限 C、一、三、四象限 D、二、三、四象限5. 为了调查某校学生的视力情况,在全校的1000名学生中随机抽取了80名学生,下列说法正确的是( )A、此次调查属于全面调查 B、1000名学生是总体 C、样本容量是80 D、被抽取的每一名学生称为个体6. 已知点 在第四象限,且点 到 轴, 轴的距离分别为 .则点 的坐标为( )A、 B、 C、 D、7. 如图,菊花1角硬币为外圆内正九边形的边缘异形币,则该正九边形的一个内角的大小为( )
A、12 B、15 C、18 D、214. 在平面直角坐标系中,函数 的图象经过( )A、一、二、三象限 B、一、二、四象限 C、一、三、四象限 D、二、三、四象限5. 为了调查某校学生的视力情况,在全校的1000名学生中随机抽取了80名学生,下列说法正确的是( )A、此次调查属于全面调查 B、1000名学生是总体 C、样本容量是80 D、被抽取的每一名学生称为个体6. 已知点 在第四象限,且点 到 轴, 轴的距离分别为 .则点 的坐标为( )A、 B、 C、 D、7. 如图,菊花1角硬币为外圆内正九边形的边缘异形币,则该正九边形的一个内角的大小为( ) A、 B、 C、 D、8. 已知四边形 是平行四边形,下列结论中正确的个数有( )
A、 B、 C、 D、8. 已知四边形 是平行四边形,下列结论中正确的个数有( )①当 时,它是菱形;②当 时,它是菱形;③当 时,它是矩形;④当 时,它是正方形.
A、4 B、3 C、2 D、19. 快车从甲地驶往乙地,慢车从乙地驶往甲地,两车同时出发并且在同一条公路上匀速行驶.图中折线表示快、慢两车之间的路程 与它们的行驶时间 之间的函数关系.小欣同学结合图像得出如下结论:①快车途中停留了 ;②快车速度比慢车速度多 ;③图中 ;④快车先到达目的地.其中正确的是( )
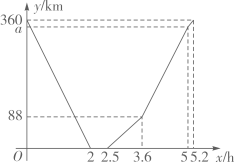 A、①③ B、②③ C、②④ D、①④10. 如图所示, 的周长是 ,对角线 与 交于点 , , 是 的中点, 的周长比 的周长多 ,则 的长度为( )
A、①③ B、②③ C、②④ D、①④10. 如图所示, 的周长是 ,对角线 与 交于点 , , 是 的中点, 的周长比 的周长多 ,则 的长度为( )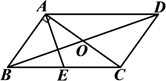 A、 B、 C、 D、11. 一次函数 的图象如图所示,则下列结论正确的是( )
A、 B、 C、 D、11. 一次函数 的图象如图所示,则下列结论正确的是( )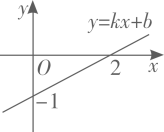 A、 B、 C、 随 的增大而减小 D、当 时,12. 如图所示,在矩形 中, , ,将矩形沿 折叠,点 落在点 处, 与 交于点 ,则重叠部分 的面积是( )
A、 B、 C、 随 的增大而减小 D、当 时,12. 如图所示,在矩形 中, , ,将矩形沿 折叠,点 落在点 处, 与 交于点 ,则重叠部分 的面积是( ) A、20 B、16 C、12 D、10
A、20 B、16 C、12 D、10二、填空题
-
13. 函数 自变量的取值范围是 .14. 如图,若在象棋棋盘上建立平面直角坐标系,使“兵”位于点 ,“炮”位于点 ,则“马”位于点 .
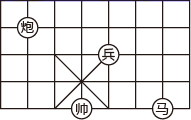 15. 为了统计了解某市4万名学生平均每天读书时间,有以下步骤:①得出结论,提出建议;②分析数据;③从4万名学生中随机抽取400名学生,调查他们平均每天读书时间;④利用统计图表将收集的数据整理和表示,请您对以上步骤进行合理排序 .16. 如图,直线 经过点 ,当 时, 的取值范围为 .
15. 为了统计了解某市4万名学生平均每天读书时间,有以下步骤:①得出结论,提出建议;②分析数据;③从4万名学生中随机抽取400名学生,调查他们平均每天读书时间;④利用统计图表将收集的数据整理和表示,请您对以上步骤进行合理排序 .16. 如图,直线 经过点 ,当 时, 的取值范围为 .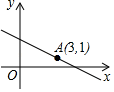 17. 已知菱形 的周长为 ,且相邻两内角之比是 ,则菱形的面积是 .18. 如图(1)是两圆柱形联通容器(联通处体积忽略不计),向甲容器匀速注水,甲容器的水面高度h(cm)随时间t(分)之间的函数关系如图(2)所示,根据提供的图象信息,若甲容器的底面半径为1cm,则乙容器的底面半径为cm.
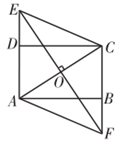
17. 已知菱形 的周长为 ,且相邻两内角之比是 ,则菱形的面积是 .18. 如图(1)是两圆柱形联通容器(联通处体积忽略不计),向甲容器匀速注水,甲容器的水面高度h(cm)随时间t(分)之间的函数关系如图(2)所示,根据提供的图象信息,若甲容器的底面半径为1cm,则乙容器的底面半径为cm.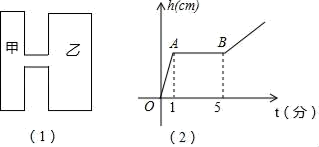 19. 如图,在正八边形 中,对角线 的延长线与边 的延长线交于点M,则 的大小为 .
19. 如图,在正八边形 中,对角线 的延长线与边 的延长线交于点M,则 的大小为 . 20. 如图,点A ,点 第一次跳动到点 ,第二次向右跳动3个单位至点 ,第三次跳动至点 ,第四次向右跳动5个单位至点 ,依此规律跳动下去,点 第2021次跳动至点 的坐标是 .
20. 如图,点A ,点 第一次跳动到点 ,第二次向右跳动3个单位至点 ,第三次跳动至点 ,第四次向右跳动5个单位至点 ,依此规律跳动下去,点 第2021次跳动至点 的坐标是 .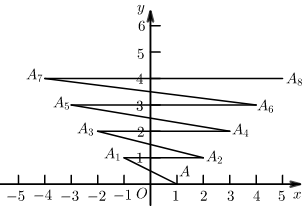
三、解答题
-
21. 已知,在平面直角坐标系中,三角形ABC三个顶点的坐标分别为 , , .请在所给的平面直角坐标系中按要求完成以下问题:
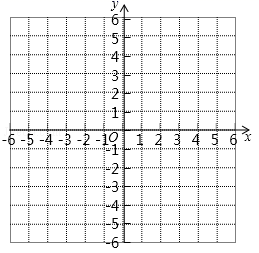 (1)、画出三角形ABC;(2)、将三角形ABC先向下平移6个单位长度,再向左平移3个单位长度后得到的三角形 (点 , , 分别是点A,B,C移动后的对应点)请画出三角形 ;并判断线段AC与 位置与数量关系.22. 李大爷按每千克2.1元批发了一批黄瓜到镇上出售,为了方便,他带了一些零钱备用.他先按市场售出一些后,又降低出售.售出黄瓜千克数x与他手中持有的钱数y元(含备用零钱)的关系如图所示,结合图象回答下列问题:
(1)、画出三角形ABC;(2)、将三角形ABC先向下平移6个单位长度,再向左平移3个单位长度后得到的三角形 (点 , , 分别是点A,B,C移动后的对应点)请画出三角形 ;并判断线段AC与 位置与数量关系.22. 李大爷按每千克2.1元批发了一批黄瓜到镇上出售,为了方便,他带了一些零钱备用.他先按市场售出一些后,又降低出售.售出黄瓜千克数x与他手中持有的钱数y元(含备用零钱)的关系如图所示,结合图象回答下列问题: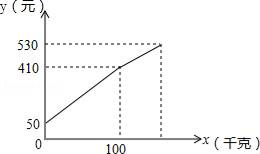 (1)、李大爷自带的零钱是多少?(2)、降价前他每千克黄瓜出售的价格是多少?(3)、卖了几天,黄瓜卖相不好了,随后他按每千克下降1.6元将剩余的黄瓜售完,这时他手中的钱(含备用的钱)是530元,问他一共批发了多少千克的黄瓜?(4)、请问李大爷亏了还是赚了?若亏(赚)了,亏(赚)多少钱?23. 某地区为提倡节约用水,准备实行自来水“阶梯计费”方式,用户用水不超出基本用水量的部分享受基本价格,超出基本用水量的部分实行加价收费,为更好的决策,自来水公司随机抽取了部分用户的用水量数据,并绘制了如图所示的不完整的统计图(每组数据包括右端点但不包括左端点).
(1)、李大爷自带的零钱是多少?(2)、降价前他每千克黄瓜出售的价格是多少?(3)、卖了几天,黄瓜卖相不好了,随后他按每千克下降1.6元将剩余的黄瓜售完,这时他手中的钱(含备用的钱)是530元,问他一共批发了多少千克的黄瓜?(4)、请问李大爷亏了还是赚了?若亏(赚)了,亏(赚)多少钱?23. 某地区为提倡节约用水,准备实行自来水“阶梯计费”方式,用户用水不超出基本用水量的部分享受基本价格,超出基本用水量的部分实行加价收费,为更好的决策,自来水公司随机抽取了部分用户的用水量数据,并绘制了如图所示的不完整的统计图(每组数据包括右端点但不包括左端点).用户用水量频数分布直方图
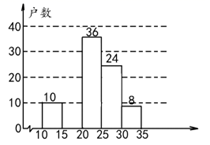
用户用水量扇形统计图
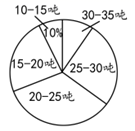
请你根据统计图解答下列问题:
(1)、此次抽样调查的样本容量是;(2)、补全频数分布直方图,求扇形图中“ 吨”部分对应的圆心角的度数;(3)、如果自来水公司将基本用水量定为每户25吨,那么该地区6万用户中约有多少用户的用水全部享受基本价格?