河北省沧州市河间市2020-2021学年八年级下学期数学期末试卷

试卷更新日期：2021-08-16 类型：期末考试

进入出卷网下载

一、单选题

1. 下列各式是最简二次根式的是（）

A、 $\sqrt{13}$ B、 $\sqrt{12}$ C、 $\sqrt{a^{2}}$ D、 $\sqrt{\frac{5}{3}}$

查看试题解析
2. 如图是一株美丽的勾股树，其中所有的四边形都是正方形，所有的三角形都是直角三角形．若正方形A，B，C，D的边长分别是3，5，2，3，则最大正方形E的面积是（）

A、13 B、26 C、47 D、94

查看试题解析
3. 工人师傅在做门窗或矩形零件时，不仅要测量两组对边的长度是否分别相等，常常还要测量它们的两条对角线是否相等，以确保图形是矩形．这样做的道理是（）

A、两组对边分别相等的四边形是矩形 B、有一个角是直角的平行四边形是矩形 C、对角线相等的四边形是矩形 D、对角线相等的平行四边形是矩形

查看试题解析
4. 一次函数 $y = - 3 x + 1$ 的图象过点 $(x_{1} ， y_{1})$ ， $(x_{1} + 1 ， y_{2})$ ， $(x_{1} + 2 ， y_{3})$ ，则（）

A、 $y_{1} < y_{2} < y_{3}$ B、 $y_{3} < y_{2} < y_{1}$ C、 $y_{2} < y_{1} < y_{3}$ D、 $y_{3} < y_{1} < y_{2}$

查看试题解析
5. 一组数字2，4，6，x，3，9，它的众数为3，求这组数字的中位数（）

A、3 B、3.5 C、4 D、5

查看试题解析
6. 函数y= $\sqrt{x - 4}$ 中自变量x的取值范围是（）

A、x≥0 B、x≥4 C、x≤4 D、x>4

查看试题解析
7. 菱形的两条对角线的长分别是6和8 ，则这个菱形的周长是（）

A、24 B、20 C、10 D、25

查看试题解析
8. 顺次连接四边形ABCD各边中点E、F、G、H，若四边形EFGH为菱形，则四边形ABCD必须满足条件（）

A、四边形ABCD是平行四边形 B、四边形ABCD是矩形 C、四边形ABCD是菱形 D、AC＝BD

查看试题解析
9. 定义：点A（x，y）为平面直角坐标系内的点，若满足x=y，则把点A叫做“平衡点”．例如：M（1，1），N（-2，-2），都是“平衡点”．当 $- 1 \leq x \leq 3$ 时，直线 $y = 2 x + m$ 上有“平衡点”，则 $m$ 的取值范围是（）．

A、 $0 \leq m \leq 1$ B、 $- 3 \leq m \leq 1$ C、 $- 3 \leq m \leq 3$ D、 $- 1 \leq m \leq 0$

查看试题解析
10. 在战“疫”诗歌创作大赛中，有7名同学进入了决赛，他们的最终成绩均不同.小弘同学想知道自己能否进入前3名，除要了解自己的成绩外，还要了解这7名同学成绩的（）

A、中位数 B、平均数 C、众数 D、方差

查看试题解析
11. 已知等腰△OAB的面积为3，其底边OB在x轴上，且点B的坐标为（2，0），点A在第四象限，则OA所在的直线的解析式为（）

A、y＝3x B、y＝﹣3x C、y＝ $\frac{3}{2}$ x D、y＝﹣ $\frac{3}{2}$ x

查看试题解析
12. 某天小明骑自行车上学，途中因自行车发生故障，修车耽误了一段时间后继续骑行，按时赶到了学校.如图描述了他上学的情景，下列说法中错误的是（）

A、自行车发生故障时离家距离为1000米 B、学校离家的距离为2000米 C、到达学校时共用时间20分钟 D、修车时间为15分钟

查看试题解析
13. 一次数学测试，某小组五名同学的成绩如下表所示（有两个数据被遮盖）
同学
A
B
C
D
E
方差
平均成绩
得分
81
79
80
82
80
那么被遮盖的两个数据依次是（）

A、78，2 B、78， $\sqrt{2}$ C、80，2 D、80， $\sqrt{2}$

查看试题解析
14. 定义：点A（x，y）为平面直角坐标系内的点，若满足x=y，则把点A叫做“平衡点”．例如：M（1，1），N（﹣2，﹣2）都是“平衡点”．当﹣1≤x≤3时，直线y=2x+m上有“平衡点”，则m的取值范围是（）

A、0≤m≤1 B、﹣3≤m≤1 C、﹣3≤m≤3 D、﹣1≤m≤0

查看试题解析

二、填空题

15. 已知x=2- $\sqrt{2}$ ，则代数式x²-2x-1的值为．

查看试题解析
16. 如图在边长为acm的正方形ABCD中，E为BC上一点，EF⊥AC于点F，EG⊥BD于点G，那么EF＋EG＝cm．

查看试题解析
17. 如图，直线y＝－x＋m与y＝nx＋4n（n≠0）的交点的横坐标为－2，则关于x的不等式－x＋m＞nx＋4n的解集为．

查看试题解析
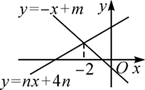18. 随机从甲、乙两块试验田中各抽取100株麦苗测量高度，计算平均数和方差的结果为： $\bar{x}$ _甲= $\bar{x}$ _乙 $= 10$ ，S²_甲=3.5，S²_乙=3.2，则小麦长势比较整齐的试验田是．

查看试题解析
19. 七一快到了，为了庆祝建党一百周年，同学们做了许多拉花布置教室，小明搬来一架高为2.5m的木梯，想把拉花挂到2.4m 的墙上，则梯角应距墙角m．

查看试题解析

三、解答题

20. 计算

(1)、 $\frac{1}{\sqrt{2} - 1}$ ＋ $\sqrt{3}$ （ $\sqrt{3}$ － $\sqrt{6}$ ）＋ $\sqrt{8}$

(2)、（ $\sqrt{3}$ －1）（ $\sqrt{3}$ ＋1）－（ $\sqrt{18}$ －24）÷ $\sqrt{6}$

查看试题解析
21. 古希腊的哲学家柏拉图曾指出，如果 $m$ 表示大于1的整数， $a = 2 m$ ， $b = m^{2} - 1$ ， $c = m^{2} + 1$ ，那么 $a ， b ， c$ 为勾股数．你认为对吗？如果对，你能利用这个结论得出一些勾股数吗？

查看试题解析

22. 随机抽取某小吃店一周的营业额（单位：元）如下表：

星期一	星期二	星期三	星期四	星期五	星期六	星期日	合计
540	680	640	640	780	1110	1070	5460

(1)、分析数据，填空：这组数据的平均数是元，中位数是元，众数是元．

(2)、估计一个月的营业额（按30天计算）：

①星期一到星期五营业额相差不大，用这5天的平均数估算合适么： ▲ ．（填“合适”或“不合适”）

②选择一个你认为最合适的数据估算这个小吃店一个月的营业额．

查看试题解析

23. 如图，四边形ABCD是正方形，点E是边BC的中点，∠AEF＝90°，且EF交正方形外角的平分线CF于点F．求证AE＝EF．
（提示：取AB的中点H，连接EH．）

查看试题解析

24. 问题：探究函数y=|x|﹣2的图象与性质．

小华根据学习函数的经验，对函数y=|x|﹣2的图象与性质进行了探究．

下面是小华的探究过程，请补充完整：

在函数y=|x|﹣2中，自变量x可以是任意实数；

(1)、如表是y与x的几组对应值．

x	…	﹣3	﹣2	﹣1	0	1	2	3	…
y	…	1	0	﹣1	﹣2	﹣1	0	m	…

①m= ；

②若A（n，8），B（10，8）为该函数图象上不同的两点，则n= ；

(2)、如图，在平面直角坐标系xOy中，描出以上表中各对对应值为坐标的点．并根据描出的点，画出该函数的图象；

根据函数图象可得：

①该函数的最小值为 ▲ ；

②已知直线 $y_{1} = \frac{1}{2} x - \frac{1}{2}$ 与函数y=|x|﹣2的图象交于C、D两点，当y₁≥y时x的取值范围是 ▲ ．

查看试题解析

25. 在正方形ABCD的边AB上任取一点E，作EF⊥AB交BD于点F，取FD的中点G，连接EG、CG，如图（1），易证 EG=CG且EG⊥CG

(1)、将△BEF绕点B逆时针旋转90°，如图（2），则线段EG和CG有怎样的数量关系和位置关系？请直接写出你的猜想．

(2)、将△BEF绕点B逆时针旋转180°，如图（3），则线段EG和CG又有怎样的数量关系和位置关系.请写出你的猜想，并加以证明．

查看试题解析

同学	A	B	C	D	E	方差	平均成绩
得分	81	79		80	82		80