河北省保定市高碑店市2020-2021学年八年级下学期数学期末试卷

试卷更新日期：2021-08-16 类型：期末考试

进入出卷网下载

一、单选题

1. 下列变形中，正确的是（）

A、 $\frac{b}{a} = \frac{b c}{a c}$ B、 $\frac{1}{a} - \frac{1}{b} = \frac{1}{a - b}$ C、 $\frac{b m^{2}}{a m^{2}} = \frac{b}{a}$ D、 $\frac{a + a b}{b + a b} = \frac{a}{b}$

查看试题解析
2. 下列图形中，既是中心对称图形又是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 下列因式分解正确的是（）

A、x²﹣4x﹣4＝（x﹣2）² B、﹣4a²+9b²＝（﹣2a+3b）（2a+3b） C、（a+b）（a﹣b）＝a²﹣b² D、x³﹣x＝x（x²﹣1）

查看试题解析
4. ▱ABCD的周长为36 cm，AB= $\frac{5}{7}$ BC，则较长边的长为（）

A、15 cm B、7.5 cm C、21 cm D、10.5 cm

查看试题解析
5. 下列命题中的真命题是（）

A、两锐角对应相等的两个直角三角形全等 B、如果四边形的一组对角互补，那么另一组对角不一定互补 C、有一个角等于60°的等腰三角形是等边三角形 D、一组对边平行，另一组对边相等的四边形是平行四边形

查看试题解析
6. 如图，已知 $B D$ 是 $△ A B C$ 的角平分线， $E D$ 是 $B C$ 的垂直平分线， $∠ B A C = 90 °$ ， $A D = 3$ ，则 $C E$ 的长为（）

A、6 B、5 C、4 D、 $3 \sqrt{3}$

查看试题解析
7. 老师设计了接力游戏，用合作的方式完成分式化简，规则是：每人只能看到前一人给的式子，并进行一步计算，再将结果传递给下一人，最后完成化简．过程如图所示：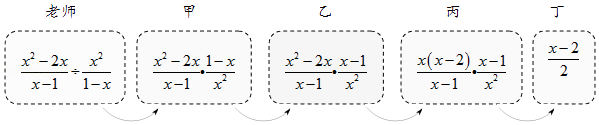
接力中，自己负责的一步出现错误的是（）

A、只有乙 B、甲和丁 C、乙和丙 D、乙和丁

查看试题解析
8. 如图，直线 $y = k x + b (k \neq 0)$ 经过点 $(- 1 ， 3)$ ，则不等式 $k x + b \geq 3$ 的解集为（）

A、 $x > - 1$ B、 $x < - 1$ C、 $x \geq 3$ D、 $x \geq - 1$

查看试题解析
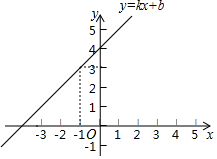9. 不等式组 ${\begin{array}{l} 2 x - 6 < 3 x \\ \frac{x + 2}{5} - \frac{x - 1}{4} \geq 0 \end{array}$ 的解集在数轴上表示正确的是（）

A、 B、 C、 D、

查看试题解析
10. 小明同学在计算某n边形的内角和时，不小心少输入一个内角，得到和为2005°．则n等于（　　）

A、11 B、12 C、13 D、14

查看试题解析
11. 如图，▱ABCD的对角线AC，BD相交于点O，点E是AB的中点，△BEO的周长是20，则△BCD的周长为（）

A、30 B、40 C、50 D、60

查看试题解析
12. 如图，在∠MON中，以点O为圆心、任意长为半径作弧，交射线OM于点A，交射线ON于点B，再分别以A，B为圆心、OA的长为半径作弧，两弧在∠MON的内部交于点C，作射线OC，连接AB，AC．若OA＝10，AB＝12，则点B到AC的距离为（）

A、 $\frac{24}{5}$ B、4 C、5 D、 $\frac{48}{5}$

查看试题解析
13. 若关于x的不等式组 ${\begin{array}{l} 2 x - 1 < 4 x + 5 \\ x + 1 \leq m \end{array}$ 的所有整数解的和为0，则m的值不可能是（）

A、3 B、3.5 C、3.7 D、4

查看试题解析
14. 如图，线段 $A B$ 经过平移得到线段 $A^{'} B^{'}$ ，其中点 $A$ ， $B$ 的对应点分别为点 $A^{'}$ ， $B^{'}$ ，这四个点都在格点上．若线段 $A B$ 上有一个点 $P ($ $a$ ， $b)$ ，则点 $P$ 在 $A^{'} B^{'}$ 上的对应点 $P^{'}$ 的坐标为 $($ $)$

A、 $(a - 2 ， b + 3)$ B、 $(a - 2 ， b - 3)$ C、 $(a + 2 ， b + 3)$ D、 $(a + 2 ， b - 3)$

查看试题解析
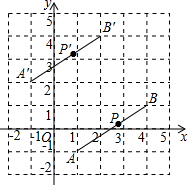15. 若关于 $x$ 的分式方程 $\frac{x}{x - 2} = 2 - \frac{m}{2 - x}$ 的解为正数，则满足条件的正整数 $m$ 的值为（）

A、 $1, 2, 3$ B、 $1, 2$ C、 $2, 3$ D、 $1, 3$

查看试题解析
16. 如图，已知 $▱ A B C D$ 的顶点A、C分别在直线 $x = 1$ 和 $x = 4$ 上，O是坐标原点，则对角线OB长的最小值为（）

A、4 B、5 C、6 D、7

查看试题解析

二、填空题

17. 要使分式 $\frac{x + 2}{x - 1}$ 有意义，则x应满足条件．

查看试题解析
18. 利用因式分解计算：（﹣2）¹⁰¹+（﹣2）¹⁰⁰＝．

查看试题解析
19. 把两个等腰直角△ABC和△ADE按如图所示的位置摆放，将△ADE绕点A按逆时针方向旋转，如图②，连接BD，EC，设旋转角为α（0°＜α＜360°）．（1）当DE⊥AC时，AE与BC的位置关系是；（2）当点D在线段BE上时，∠BEC的度数是．

查看试题解析

三、解答题

20.

(1)、解分式方程： $\frac{y - 2}{2 y - 1} = 1 - \frac{3}{1 - 2 y}$ ；

(2)、解不等式组 ${\begin{array}{l} 2 x - 3 < x ① \\ 1 - \frac{x}{3} \leq \frac{x + 12}{6} ② \end{array}$ ，并写出它的所有整数解．

查看试题解析
21.

(1)、先因式分解，再求值： ${(\frac{x + y}{2})}^{2} - {(\frac{x - y}{2})}^{2}$ ，其中 $x = - \frac{2}{3}$ ， $y = \frac{1}{4}$ ．

(2)、已知正方形的面积是9x²+12xy+4y²（x＞0，y＞0），利用因式分解写出表示该正方形的边长的代数式．

查看试题解析
22. 如图，在平面直角坐标系中，Rt△ABC的三个顶点分别是A（﹣4，1），B（﹣1，3），C（﹣1，1）．

(1)、将△ABC以点C为旋转中心旋转180°，画出旋转后对应的△A₁B₁C₁；平移△ABC，若点A对应的点A₂的坐标为（﹣4，﹣5），画出△A₂B₂C₂ ．

(2)、若△A₁B₁C₁ ，绕某一点旋转可以得到（1）中的△A₂B₂C₂ ，直接写出旋转中心的坐标：；

(3)、若D为BC中点，在x轴上有一点P使得PA+PD的值最小，直接写出点P的坐标：．

查看试题解析
23. 甲、乙两公司全体员工踊跃参与“携手防疫，共渡难关”捐款活动，甲公司共捐款100000元，乙公司共捐款140000元．下面是甲、乙两公司员工的一段对话：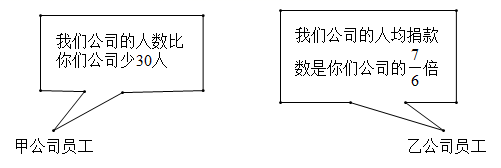

(1)、甲、乙两公司各有多少人？

(2)、现甲、乙两公司共同使用这笔捐款购买 $A$ 、 $B$ 两种防疫物资， $A$ 种防疫物资每箱15000元， $B$ 种防疫物资每箱12000元．若购买 $B$ 种防疫物资不少于10箱，并恰好将捐款用完，有几种购买方案？请设计出来（注： $A$ 、 $B$ 两种防疫物资均需购买，并按整箱配送）．

查看试题解析
24. 如图，已知：AD平分∠CAE，AD∥BC．

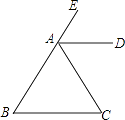(1)、求证：△ABC是等腰三角形．

(2)、当∠CAE等于多少度时△ABC是等边三角形？证明你的结论．

查看试题解析
25. 如图，在四边形ABCD中， $A D / / B C$ ，AC与BD交于点E，点E是BD的中点，延长CD到点F，使 $D F = C D$ ，连接AF．

(1)、求证：AE＝CE；

(2)、求证：四边形ABDF是平行四边形；

(3)、若AB＝4，AF＝8，∠F＝30°，则四边形ABCF的面积为．

查看试题解析
26. 如图，在△ABC中，∠ACB＝90°，AC＝a，BC＝b，a＞b，点P是边AB上一点，连接CP，将△ACP沿CP翻折得到△QCP．

(1)、若PQ⊥AB，由折叠性质可得∠BPC＝°；

(2)、若a＝8，b＝6，且PQ⊥AB，求C到AB的距离及BP的长；

(3)、连接BQ，若四边形BCPQ是平行四边形，直接写出a与b之间的关系式．

查看试题解析