广东省阳江市阳东区2020-2021学年八年级下学期数学期末试卷
试卷更新日期:2021-08-16 类型:期末考试
一、单选题
-
1. 函数 的自变量x的取值范围是( )A、 B、 C、 D、2. 下面各点中,在直线 上的是( )A、(2,1) B、( ,2) C、(1,2) D、( , )3. 直线y=kx+2过点(﹣1,4),则k的值是( )A、﹣2 B、﹣1 C、1 D、24. 下列各式计算正确的是( )A、 B、 C、 D、5. 某区学生在“垃圾分类知识”线上答题活动中,甲、乙、丙、丁四所学校参加线上答题的人数相同,四所学校答题所得分数的平均数和方差的数值如表:
选手
甲
乙
丙
丁
平均数
87
87
87
87
方差
0.027
0.043
0.036
0.029
则这四所学校成绩发挥最稳定的是( )
A、甲 B、乙 C、丙 D、丁6. 已知两点 , 都在直线 上,则 、 的大小关系是( )A、 B、 C、 D、不能确定7. 任意给定一个非零实数,按下列程序计算,最后输出的结果是( ) A、 B、 C、 D、8. 已知一次函数 (a、b是常数),x与y的部分对应值如下表:
A、 B、 C、 D、8. 已知一次函数 (a、b是常数),x与y的部分对应值如下表:0
1
2
3
0
2
4
6
8
下列说法中,错误的是( )
A、图象经过第一、二、三象限 B、函数值y随自变量x的增大而减小 C、方程 的解是 D、不等式 的解集是9. 如图,正方形网格中,每个小正方形的边长为1,则网格上的三角形ABC中,边长为无理数的边数是( )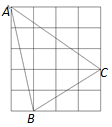 A、0 B、1 C、2 D、310. 如图,在边长为2的菱形ABCD中,∠B=45°,AE为BC边上的高,将△ABE沿AE所在直线翻折得△AB′E,AB′与CD边交于点F,则B′F的长度为( )
A、0 B、1 C、2 D、310. 如图,在边长为2的菱形ABCD中,∠B=45°,AE为BC边上的高,将△ABE沿AE所在直线翻折得△AB′E,AB′与CD边交于点F,则B′F的长度为( )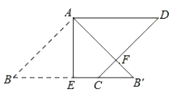 A、1 B、 C、2- D、2 ﹣2
A、1 B、 C、2- D、2 ﹣2二、填空题
-
11. 数据80,82,79,81,81的众数是 , 中位数是 .12. 某函数的图象经过(1, ),且函数y的值随自变量x的值增大而增大.请你写出一个符合上述条件的函数关系式: .13. 如图,数轴上点A表示的数为a,化简: =
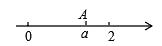 14. 如图,在 中, ,则三个半圆面积S1 , S2 , S3的关系为 .
14. 如图,在 中, ,则三个半圆面积S1 , S2 , S3的关系为 .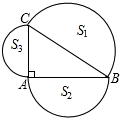 15. 某次射击训练中,一小组的成绩如下表所示:
15. 某次射击训练中,一小组的成绩如下表所示:环数
6
7
8
9
人数
1
3
2
若该小组的平均成绩为7.7环,则成绩为8环的人数是 .
16. 某书定价25元,如果一次购买20本以上,超过20本的部分打八折,试写出付款金额y(单位:元)与购书数量x(单位:本)之间的关系:.17. 如图,在平面直角坐标系中,菱形OABC的一个顶点在原点O处,且∠AOC=60°,A点的坐标是(0,4),则直线AC的表达式是 .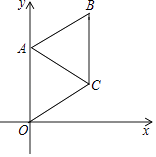
三、解答题
-
18. 计算: .19. 如图所示,正比例函数图象经过点A,求这个正比例函数的解析式.
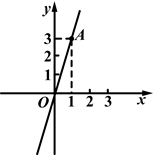 20. 某学校在开展“节约每一滴水”的活动中,从七年级的180名同学中任选出10名同学汇报了各自家庭一个月的节水情况,将有关数据整理如下表:
20. 某学校在开展“节约每一滴水”的活动中,从七年级的180名同学中任选出10名同学汇报了各自家庭一个月的节水情况,将有关数据整理如下表:节水量/t
0.5
1
1.5
2
同学数
2
3
4
1
请你估计这180名同学的家庭一个月节约用水的总量是多少?
21. 用8cm长的细铁丝围成一个等腰三角形,腰长为xcm,底边长为ycm.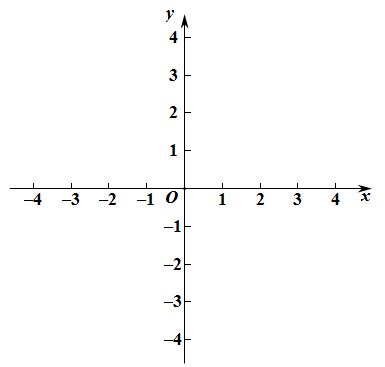 (1)、求y关于x的函数解析式;(2)、在如图的平面直角坐标系中画出该函数的图象.22. 如图,在Rt△ABC中,∠C=90°,AB=5 cm,AC=3 cm,动点P从点B出发沿射线BC以1 cm/s的速度移动,设运动的时间为t s.
(1)、求y关于x的函数解析式;(2)、在如图的平面直角坐标系中画出该函数的图象.22. 如图,在Rt△ABC中,∠C=90°,AB=5 cm,AC=3 cm,动点P从点B出发沿射线BC以1 cm/s的速度移动,设运动的时间为t s.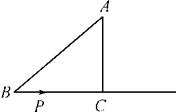 (1)、求BC边的长;(2)、当△ABP为直角三角形时,求t的值.23. 如图,在菱形ABCD中,点O是对角线AC的中点,过点O的直线EF与边AD、BC分别交于点E、F, ,连接AF、CE.
(1)、求BC边的长;(2)、当△ABP为直角三角形时,求t的值.23. 如图,在菱形ABCD中,点O是对角线AC的中点,过点O的直线EF与边AD、BC分别交于点E、F, ,连接AF、CE.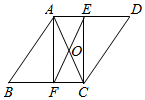 (1)、求证:四边形AFCE是矩形;(2)、若 , ,求出四边形AFCE的面积.24. 为切实加强中小学生交通安全宣传教育,让学生真正知危险、会避险,郑州市某中学开展了“交通安全进校园”系列活动.为了解七、八年级学生对交通安全知识的掌握情况,对七、八年级学生进行了测试,现从两年级中各随机抽取20名学生的测试成绩(百分制)进行整理、描述和分析(成绩不低于90分为优秀).
(1)、求证:四边形AFCE是矩形;(2)、若 , ,求出四边形AFCE的面积.24. 为切实加强中小学生交通安全宣传教育,让学生真正知危险、会避险,郑州市某中学开展了“交通安全进校园”系列活动.为了解七、八年级学生对交通安全知识的掌握情况,对七、八年级学生进行了测试,现从两年级中各随机抽取20名学生的测试成绩(百分制)进行整理、描述和分析(成绩不低于90分为优秀).测试成绩(百分制)如下:
七年级:52,78,82,86,77,83,92,87,72,81,93,98,81,69,87,86,80,81,82,94
八年级:87,77,90,79,93,83,88,84,82,94,86,88,57,68,89,59,81,90,88,95
分组整理,描述数据
分组
七年级
八年级
画“正”计数
频数
画“正”计数
频数
一
1
2
一
1
一
1
2
正正
10
4
正
5
下表为七、八年级抽取学生的测试成绩统计表
年级
平均数
中位数
众数
优秀率
七年级
82
81
20%
八年级
82.5
86.5
25%
根据以上信息,回答下列问题:
(1)、表中 , , , ;(2)、若该校七年级270人和八年级280人参加了此次测试,估计参加此次测试成绩优秀的学生人数;(3)、根据以上数据,你认为该校七、八年级哪个年级学生掌握交通安全知识较好?并说明理由?25. 如图,把矩形纸片OABC放入平面直角坐标系中,使OA,OC分别落在x轴、y轴的正半轴上,连接AC,且 , .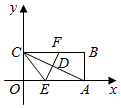 (1)、求点A,C的坐标;(2)、将矩形纸片OABC折叠,使点A与点C重合(折痕为EF),求折叠后纸片重叠部分 的面积.(3)、求EF所在直线的函数解析式.
(1)、求点A,C的坐标;(2)、将矩形纸片OABC折叠,使点A与点C重合(折痕为EF),求折叠后纸片重叠部分 的面积.(3)、求EF所在直线的函数解析式.