广东省深圳市龙华区2020-2021学年八年级下学期数学期末试卷

试卷更新日期：2021-08-16 类型：期末考试

进入出卷网下载

一、单选题

1. 若分式 $\frac{1}{x - 5}$ 有意义，则x满足的条件是（）

A、x＝0 B、x≠0 C、x＝5 D、x≠5

查看试题解析
2. 若x＜y，则下列结论错误的是（）

A、x+2＜y+2 B、2﹣x＜2﹣y C、2x＜2y D、 $\frac{x}{2} < \frac{y}{2}$

查看试题解析
3. 下列图案中，既是轴对称图形，又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
4. 已知a﹣b＝3，a+b＝2，则a²﹣b²的值为（）

A、6 B、−6 C、5 D、−5

查看试题解析
5. 图1是一张等腰直角三角形纸片，直角边的长度为2cm，用剪刀沿一直角边和斜边的中点连线（图中虚线）剪开后，拼成如图2的四边形，则该四边形的周长为（）

A、6cm B、4cm C、（4+2 $\sqrt{2}$ ）cm D、（4+ $\sqrt{2}$ ）cm

查看试题解析
6. 不等式组 ${\begin{array}{l} 2 x > 0 \\ x - 2 \leq 1 \end{array}$ 的解集在数轴上表示为（）

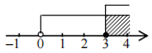A、 B、 C、 D、

查看试题解析
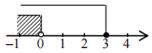7. 下列命题是真命题的是（）

A、平移既不改变图形的位置，也不改变图形的大小 B、一组对边平行，另一组对边相等的四边形是平行四边形 C、如果过多边形的一个顶点能画6条对角线，那么这个多边形是六边形 D、斜边及一锐角分别相等的两个直角三角形全等

查看试题解析
8. 甲、乙两位同学分别用尺规作图法作∠AOB的平分线OC，则他们两人的作图方法（）

A、甲、乙两人均正确 B、甲正确，乙不正确 C、甲不正确，乙正确 D、甲、乙两人均不正确

查看试题解析
9. 某校拟用不超过2600元的资金在新华书店购买党史和改革开放史书籍共40套来供学生借阅，其中党史每套72元，改革开放史每套60元，那么学校最多可以购买党史书籍多少套？设学校可以购买党史书籍x套，根据题意得（）

A、72x+60（40﹣x）≤2600 B、72x+60（40﹣x）＜2600 C、72x+60（40﹣x）≥2600 D、72x+60（40﹣x）＝2600

查看试题解析
10. 如图，已知平行四边形ABCD中，3AB＝2BC，点O是∠BAD和∠CBA的角平分线的交点，过点O作EF $//$ AB，分别交AD、BC于E、F两点，连接OD、OC．则下列结论：①AO⊥BO；②点O是EF的中点；③DE＝2AE；④S_△OCD＝4S_△OAE ，其中正确的有（）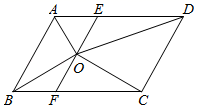

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

11. 因式分解：a³－a=.

查看试题解析
12. 如果一个多边形的每个外角都是40°，那么这个多边形是边形．

查看试题解析
13. 如图，AB是一条东西走向的海岸线，在码头A的北偏东60°且距离该码头50海里的C处有一艘轮船，该轮船正以20海里/时的速度向海岸AB驶来，那么该轮船到达海岸AB所需要的最少时间为小时．

查看试题解析
14. 如图，已知函数y＝k₁x+b₁与函数y＝k₂x+b₂的图象交于点A（﹣2，1），则关于x的不等式k₁x+b₁＞k₂x+b₂的解集是．

查看试题解析
15. 如图，已知Rt△ABC中，∠ACB＝90°，AC＝3，BC＝4，斜边AB的垂直平分线DE交AB于点D，交AC的延长线于点E，连接BE．则BE的长为．

查看试题解析

三、解答题

16.

(1)、解不等式：x﹣4＜2（2x﹣1），并写出它的最小整数解；

(2)、解不等式组： ${\begin{array}{l} 3 x + 1 < 2 x \\ \frac{x - 5}{2} + 1 > x - 3 \end{array}$ 并把它的解集在数轴上表示出来．

查看试题解析
17.

(1)、化简： $(\frac{m + 2 n}{m - n} + \frac{m}{n - m}) \div \frac{n}{m - n}$ ；

(2)、先化简，再求值：（1﹣ $\frac{1}{a^{2} - 2 a + 1}$ ）÷ $\frac{a - 2}{a - 1}$ ，其中a＝3．

查看试题解析
18. 解方程：

(1)、 $\frac{1}{x - 2} = \frac{3}{x^{2} - 4}$ ；

(2)、 $\frac{2 - y}{y - 3} = \frac{1}{3 - y} - 2$ ．

查看试题解析
19. 如图1，已知Rt△ABC的三个顶点均在网络的格点上，每个格子的边长为1个单位长度，请使用无刻度的直尺分别按如下的要求画出图形（不要求写画图步骤，但要保留画图痕迹）．

(1)、将Rt△ABC向上平移4个单位长度，再向右平移1个单位长度得到Rt△A₁B₁C₁ ，请在图1中画出平移后的Rt△A₁B₁C₁；

(2)、如图1，若将Rt△ABC绕点P沿逆时针方向旋转90°后得到Rt△A₂B₂C₂ ，请画出点P；

(3)、请在图2中画出一个以AC为一边，各顶点均在格点上，且面积为Rt△ABC的2倍的平行四边形ACEF．

查看试题解析
20. 深圳正全力争创“全国文明典范城市”，斑马线前“车让人”，不仅体现着一座城市对生命的尊重，也直接反映着城市的文明程度．某路口的斑马线路段A﹣B﹣C横穿双向行驶车道如图所示，其中AB＝BC＝6米，在绿灯亮时，小明共用11秒通过AC，其中通过BC的速度比通过AB的速度快20%．求小明通过AB时的速度．

查看试题解析
21. 如图，已知平行四边形ABCD中，∠ABC、∠ADC的角平分线分别交AD、BC于点E、F．求证：DE＝BF．

查看试题解析
22. 阅读下列材料，并解答其后的问题：
定义：有一组邻边相等且有一组对角互补的四边形叫做等补四边形．

如图1，若AB＝AD，∠A+∠C＝180°，则四边形ABCD是等补四边形．

(1)、理解：如图2，已知Rt△ABC中，∠ACB＝90°．请用尺规作图法作出点D，使得以A、B、C、D四点为顶点的四边形是等补四边形；（只需作出一个满足条件的点D即可．要求不用写作法，但要保留作图痕迹．）

(2)、探究：如图3，等补四边形ABCD中，AB＝BC，∠A+∠C＝180°，BD是对角线．求证：BD平分∠ADC；

(3)、运用：将斜边相等的两块三角板如图4放置，其中含45°角的三角板ABC的斜边与含30°角的三角板ADC的斜边重合，B、D位于AC的两侧，AB＝BC＝4，连接BD．则BD的长为．

查看试题解析
23. 如图1，在平面直角坐标系xOy中，已知平行四边形OABC的顶点O为坐标原点，顶点A在x轴的正半轴上，B、C在第一象限内，且OA＝6，OC＝3 $\sqrt{2}$ ，∠AOC＝45°．

(1)、顶点B的坐标为，顶点C的坐标为；

(2)、设对角线AC、OB交于点E，在y轴上有一点D（0，﹣1），x轴上有一长为1个单位长度的可以左右平移的线段MN，点M在点N的左侧，连接DM、EN，求DM+EN的最小值；

(3)、如图2，若直线l：y＝kx+b过点P（0，﹣2），且把平行四边形OABC的面积分成1：2的两部分，请直接写出直线l的函数解析式．

查看试题解析