广东省汕头市潮阳区2020-2021学年八年级下学期数学期末试卷

试卷更新日期：2021-08-16 类型：期末考试

进入出卷网下载

一、单选题

1. 下列二次根式中是最简二次根式的是（）

A、 $2 \sqrt{8}$ B、 $\sqrt{b^{2}}$ C、 $3 \sqrt{3}$ D、 $\sqrt{\frac{3}{4}}$

查看试题解析
2. 函数y= $\sqrt{2 x - 4}$ 中自变量x的取值范围是（）

A、x＞2 B、x≥2 C、x≤2 D、x≠2

查看试题解析
3. 无理数 $\sqrt{5}$ 的倒数是（）

A、 $- \sqrt{5}$ B、 $- \frac{\sqrt{5}}{5}$ C、 $- 5$ D、 $\frac{\sqrt{5}}{5}$

查看试题解析
4. 2022年北京张家口将举办冬季奥运会，四名短道速滑选手几次选拔赛的平均成绩均为51秒，他们的方差如下表所示，则在这四个选手中，成绩最稳定的是（）

甲

乙

丙

丁

方差s²

6.5

4.5

12.5

17.5

A、甲 B、乙 C、丙 D、丁

查看试题解析
5. 若把一次函数y=2x﹣3，向下平移3个单位长度，得到图象解析式是（）

A、y=2x B、y=2x﹣6 C、y=5x﹣3 D、y=﹣x﹣3

查看试题解析
6. 如图，有一架梯子斜靠在与地面（OM）垂直的墙（ON）上，在墙角（点O处）有一只猫紧紧盯住位于梯子（AB）正中间（点P处）的老鼠，等待与老鼠距离最小时扑捉，把梯子、猫和老鼠都理想化为同一平面内的线或点，模型如图，若梯子A端沿墙下滑，且梯子B端沿地面向右滑行．在此滑动过程中，猫与老鼠的距离（）

A、不变 B、变小 C、变大 D、无法判断

查看试题解析
7. 如图，在矩形COED中，点D的坐标是(1，3)，则CE的长是（）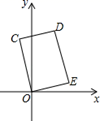

A、3 B、 $2 \sqrt{2}$ C、 $\sqrt{10}$ D、4

查看试题解析
8. 五一小长假的某一天，亮亮全家上午8时自驾小汽车从家里出发，到某旅游景点游玩，该小汽车离家的距离（千米）与时间（时）之间的关系如图所示，根据图象提供的有关信息，判断下列说法中错误的是（）

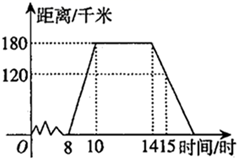A、景点离亮亮的家180千米 B、亮亮到家的时间为17时 C、小汽车返程的速度为60千米/时 D、10时至14时小汽车匀速行驶

查看试题解析
9. 如图是“赵爽弦图”，△ABH、△BCG、△CDF和△DAE是四个全等的直角三角形，四边形ABCD和EFGH都是正方形．如果AB=10，AH=6，那么EF等于（）

A、8 B、6 C、4 D、2

查看试题解析
10. 如图，已知正比例函数 $y_{1} = a x$ 与一次函数 $y_{2} = \frac{1}{2} x + b$ 的图象交于点P，则以下结论：① $a > 0$ ；② $2 a + b = 1$ ；③当 $x < 0$ 时， $y_{1} > 0$ ；④当 $x < - 2$ 时， $a x < \frac{1}{2} x + b$ ；其中正确的有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

11. 已知a、b为实数，且满足 ${(a - 2)}^{2} + \sqrt{a - b + 1} = 0$ ，计算a+b的值为．

查看试题解析
12. 如图，当AO＝OC，BD＝6cm，那么OB＝cm时，四边形ABCD是平行四边形．

查看试题解析
13. 某校招聘教师，规定综合成绩由笔试成绩和面试成绩构成，其中笔试占60%，面试占40%，有一名应聘者的综合成绩为84分，笔试成绩是80分，则面试成绩为分．

查看试题解析
14. 如图是关于x的一次函数 $y = (1 - m) x + 2 + m$ 的图象，则实数m的取值范围．

查看试题解析
15. 已知等腰三角形的的周长是12，设腰长为x，底边长为y，那么y关于x的函数关系式为（写出自变量x的取值范围）．

查看试题解析
16. 如图，把矩形ABCD沿EF翻转，点B恰好落在AD边的B′处，若AE=2，DE=6，∠EFB=60°，则矩形ABCD的面积是

查看试题解析
17. 如图，平行四边形ABCD的顶点A是等边△EFG边FG的中点，∠B=60°，EF=4，则阴影部分的面积为.

查看试题解析

三、解答题

18. 计算： $\sqrt{12} \div \frac{1}{2} \sqrt{3} - 6 \sqrt{\frac{1}{3}} \times 2 \sqrt{48}$

查看试题解析
19. 如图，在平行四边形ABCD中，AB＜BC．

(1)、在BC边上确定点P，使点P到边AB，AD的距离相等．（用尺规作图，不写作法，保留作图痕迹）；

(2)、在（1）中所作的图形中，若AB=3，AD=4，则CP= ．

查看试题解析
20. 已知 $y - 2$ 与x成正比例，且当 $x = - 2$ 时， $y = 4$ ．

(1)、求y与x的函数表达式；

(2)、在坐标系中画出（1）中的函数图象．

查看试题解析
21. 已知：如图，在△ABC中，直线PQ垂直平分AC，与边AB交于点E，连接CE，过点C作CF∥BA交PQ于点F，连接AF．

(1)、求证：四边形AECF是菱形；

(2)、若AD=3，AE=5，则求菱形AECF的面积．

查看试题解析
22. 为了解学生参加户外活动的情况，和谐中学对学生每天参加户外活动的时间进行抽样调查，并将调查结果绘制成如图两幅不完整的统计图，根据图示，请回答下列问题：

(1)、求被抽样调查的学生有多少人？并补全条形统计图；

(2)、每天户外活动时间的中位数是小时？

(3)、该校共有1850名学生，请估计该校每天户外活动时间超过1小时的学生有多少人？

查看试题解析
23. 为了预防新冠肺炎，某药店欲购进甲、乙两种防护口罩进行销售，有关信息如表：

进价（元/袋）

售价（元/袋）

甲种防护口罩

a

25

乙种防护口罩

1.5a

37

用600元购进甲种防护口罩的数量比用同样金额购进乙种防护口罩的数量多10袋．

(1)、求甲、乙两种防护口罩每袋进价分别为多少元?

(2)、该药店准备购进甲、乙两种防护口罩共40袋，且甲种防护口罩不少于30袋，问应该怎样进货，才能使总获利最大，最大利润为多少元?

查看试题解析
24. 如图1，把一个含45°角的直角三角板ECF和一个正方形ABCD摆放在一起，使三角板的直角顶点和正方形的顶点C重合，点E、F分别在正方形边CB、CD上，连接AF，取AF中点M，EF的中点N，连接MD、MN．

(1)、连接AE，则△AEF是三角形，MD、MN的数量关系是．

(2)、如图2，将图1中的直角三角板ECF绕点C顺时针旋转180°，其他条件不变，则MD、MN的数量关系还成立吗？若成立，请加以证明；若不成立，请说明理由．

(3)、将图1中正方形ABCD及直角三角板ECF同时绕点C顺时针旋转90°，如图3，其他条件不变，则MD、MN的数量关系还成立吗？若成立，请加以证明；若不成立，请说明理由．

查看试题解析
25. 如图，在平面直角坐标系中，直线 $y = \frac{3}{4} x + 6$ 与x轴交于点A，与y轴交于点B，把△COB沿BC翻折，点O恰好落在AB边的点D处，BC为折痕．

(1)、求线段AB的长；

(2)、求直线BC的解析式；

(3)、若M是射线BC上的一个动点，在坐标平面内是否存在点P，使以A、B、M、P为顶点的四边形是矩形？若存在，请直接写出点P的坐标；若不存在，请说明理由．

查看试题解析

	进价（元/袋）	售价（元/袋）
甲种防护口罩	a	25
乙种防护口罩	1.5a	37

	甲	乙	丙	丁
方差s²	6.5	4.5	12.5	17.5