广东省梅州市大埔县2020-2021学年八年级下学期数学期末试卷

试卷更新日期：2021-08-16 类型：期末考试

进入出卷网下载

一、单选题

1. 据气象台预报，2020年5月某日大埔最高气温27℃，最低气温21℃，则当天气温t（℃）的变化范围是（）

A、t＞21 B、t≤27 C、21＜t＜27 D、21≤t≤27

查看试题解析
2. 多项式 $a^{2} - 2 a$ 的公因式是（）

A、 $a$ B、 $a^{2}$ C、2 $a$ D、 $- 2 a$

查看试题解析
3. 民族图案是数学文化中的瑰宝．下列图案中，是轴对称图形但不是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
4. 若分式 $\frac{x}{x - 2}$ 有意义，则x的取值范围是（）

A、 $x > 0$ B、 $x \neq 0$ C、 $x \leq 2$ D、 $x \neq 2$

查看试题解析
5. 下列多项式能直接用完全平方公式进行因式分解的是（）

A、 $x^{2} + 2 x - 1$ B、 $x^{2} - x + \frac{1}{4}$ C、 $x^{2} + x y + y^{2}$ D、 $x^{2} - 3 x + 9$

查看试题解析
6. 如图，AE与BF交于点O，点O在CG上，根据尺规作图的痕迹，判断下列说法错误的是（）

A、AE、BF是△ABC的内角平分线 B、CG也是△ABC的一条内角平分线 C、AO＝BO＝CO D、点O到△ABC三边的距离相等

查看试题解析
7. 不等式组 ${\begin{array}{l} x + 3 \geq 0 \\ x - 2 < 0 \end{array}$ 的解集是（）

A、 $x \geq - 3$ B、 $x < 2$ C、 $- 3 < x \leq 2$ D、 $- 3 \leq x < 2$

查看试题解析
8. 如图， $▱$ $A B C D$ 的对角线AC，BD相交于点O， $E$ 是AB中点，且AE+EO=4，则 $▱ A B C D$ 的周长为（）

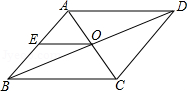A、20 B、16 C、12 D、8

查看试题解析
9. 顺次连接平面上 $A ， B ， C ， D$ 四点得到一个四边形，从① $A D / / B C$ ，② $A B = C D$ ，③ $∠ A = ∠ C$ ，④ $∠ B = ∠ D$ 四个条件中任取其中两个，可以得出“四边形 $A B C D$ 是平行四边形”，这一结论的情况共有（）

A、2种 B、3种 C、4种 D、5种

查看试题解析
10. 如图，在 $△ A B C$ 中， $A B = A C$ ， $B C = 8 c m$ ，AE平分 $∠ B A C$ ，交 $B C$ 于点 $E$ ， $D$ 为AE上一点，且 $∠ A C D = ∠ C A D$ ， $D E = 3 c m$ ，连接 $C D$ ．过点作 $D F ⊥ A B$ ，垂足为点 $F$ ．则下列结论正确的有（）
① $C D = 5 c m$ ；② $A C = 10 c m$ ；③ $D F = 3 c m$ ；④ $△ A C D$ 的面积为 $10 c m^{2}$

A、1 B、2 C、3 D、4

查看试题解析

二、填空题

11. 分解因式： $x^{3} y - x y^{3} =$ ．

查看试题解析
12. 若分式 $\frac{m^{2} - 16}{4 - m}$ 的值为0，则 $m$ 的值为．

查看试题解析
13. 一个正多边形的每个外角为60°，那么这个正多边形的内角和是。

查看试题解析
14. 在平面直角坐标系中，点A（0,1）关于原点对称的点的坐标是.

查看试题解析
15. 使不等式4x+3<x+6成立的最大整数解是．

查看试题解析
16. 如图，△ABC中，AB=5cm，AC=12cm，BC=13cm， $∠ A B C$ 与 $∠ A C B$ 的角平分线相交于点P，过点P作PD⊥BC，垂足为点D，则线段PD的长为cm．

查看试题解析
17. 下列结论正确的有（填序号）．
①如果 $a > b$ ， $c < d$ ；那么 $a - c > b - d$ ②如果 $a > b$ ；那么 $\frac{a}{b} > 1$ ③如果 $a > b$ ，那么 $\frac{1}{a} < \frac{1}{b}$ ；

④如果 $\frac{a}{c^{2}} < \frac{b}{c^{2}}$ ，那么 $a < b$ ．

查看试题解析

三、解答题

18. 分解因式： $x^{2} {(x - y)}^{2} - y^{2} {(x - y)}^{2}$ ．

查看试题解析
19. 解方程： $\frac{x}{2 x - 1} - 2 = \frac{1}{1 - 2 x}$ ．

查看试题解析
20. 解不等式组 ${\begin{array}{l} 5 x \geq 3 x - 1 \\ \frac{x + 2}{3} - 2 < \frac{x - 5}{6} \end{array}$ ，并写出它的非负整数解．

查看试题解析
21. 如图，在△ABC中，AB=AC=2，延长BC至点D，使CD=BC，连接AD，E、F分别为AC、AD中点，连接EF，若 $∠ A C D = 120 °$ ，求线段EF的长度．

查看试题解析
22. 如图，已知E是平行四边形ABCD中BC边的中点，AC是对角线，连接AE并延长，交DC的延长线于点F，连接BF．

(1)、BF∥AC．

(2)、AE=EF；

查看试题解析
23. 某超市预测某品牌饮料有销售前景，用1200元购进一批该饮料，试销售后果然供不应求，又用5400元购进这种饮料，第二批饮料的数量是第一批的3倍，但单价比第一批多2元．

(1)、第一批饮料进货单价为多少元？

(2)、若二次购进饮料按同一价格销售，两批全部售完后，获利不少于3000元，则销售单价至少为多少元？

查看试题解析
24. 如图，在△ABC 中，AB=7，BC=14，M为AC的中点，OM⊥AC 交 $∠ A B C$ 的平分线于O，OE⊥AB交BA的延长线于E，OF⊥BC．垂足为F．

(1)、求证：AE=CF．

(2)、求线段BE的长．

查看试题解析
25. 如图1，在Rt△ABC中， $∠ B = 90 °$ ，AC=60cm， $∠ A = 60 °$ ，点D从点C出发沿CA方向以4cm/s的速度向点A匀速运动，同时点E从点A出发沿AB方向以2cm/s的速度向点B匀速运动，当其中一个点到达终点时，另一个点也随之停止运动．设点D、E运动的时间是t秒（ $0 < t < 15$ ）．过点D作DF⊥BC于点F，连接DE，EF．

(1)、用含t的代数式表示下列线段：AE= ， DF= ， AD=；

(2)、判断线段EF与AC的位置关系，并说明理由；

(3)、如图2，连接AF，交DE于点O，设y为△ADO与△DFO的周长差，求y与t的函数关系式，并求当t为何值时，△ADO与△DFO的周长相等．

查看试题解析