广东省广州市荔湾区2020-2021学年八年级下学期数学期末试卷

试卷更新日期：2021-08-16 类型：期末考试

进入出卷网下载

一、单选题

1. 下列二次根式中是最简二次根式的是（）

A、 $\sqrt{12}$ B、 $\sqrt{\frac{1}{3}}$ C、 $\sqrt{a^{2} + 1}$ D、 $\sqrt{3 a^{2}}$

查看试题解析
2. 下列计算正确的是（　　）

A、 $\sqrt{2} + \sqrt{3} = \sqrt{5}$ B、 $3 \sqrt{2} - \sqrt{2} = 2$ C、 $2 + \sqrt{6} = 2 \sqrt{6}$ D、 $\sqrt{(- 4) \times (- 2)} = 2 \sqrt{2}$

查看试题解析
3. 一次函数y=2x+1的图象不经过下列哪个象限（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
4. 《九章算术》中记载：今有户不知高、广，竿不知长、短.横之不出四尺，从之不出二尺，斜之适出.问户高、广、斜各几何？译文是：今有门，不知其高、宽，有竿，不知其长、短.横放，竿比门宽长出4尺；竖放，竿比门高长出2尺；斜放，竿与门对角线恰好相等.问门高、宽、对角线长分别是多少？若设门对角线长为x尺，则可列方程为（）

A、 $x^{2} = {(x - 4)}^{2} + {(x - 2)}^{2}$ B、 $2 x^{2} = {(x - 4)}^{2} + {(x - 2)}^{2}$ C、 $x^{2} = 4^{2} + {(x - 2)}^{2}$ D、 $x^{2} = {(x - 4)}^{2} + 2^{2}$

查看试题解析
5. 如图，在平行四边形ABCD中，∠ABC的平分线交AD于E，∠BED=150°，则∠A的大小为（）

A、150° B、130° C、120° D、100°

查看试题解析
6. 已知直角三角形的两条边长分别是3和5，那么这个三角形的第三条边的长（）

A、4 B、16 C、 $\sqrt{34}$ D、4或 $\sqrt{34}$

查看试题解析
7. 平行四边形的两条对角线长分别为6和10，则平行四边形的一条边的长x的取值范围为（）

A、4＜x＜6 B、2＜x＜8 C、0＜x＜10 D、0＜x＜6

查看试题解析
8. 对于数据3，3，2，3，9，①这组数据的众数是3；②这组数据的众数与中位数的数值不等；③这组数据的中位数与平均数的数值相等；④这组数据的平均数与众数的数值相等．其中正确的结论有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
9. 两直线解析式分别为y＝5x—8与y＝—3x，则两直线与x轴围成的三角形面积为（）

A、2 B、2.4 C、3 D、4.8

查看试题解析
10. 如图，正方形ABCD的边长为8，M在DC上，且DM=2，N是AC上的一动点，则DN+MN的最小值是（）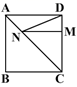

A、8 B、9 C、10 D、12

查看试题解析

二、填空题

11. 函数y= $\sqrt{x + 2}$ 中，自变量x的取值范围是．

查看试题解析
12. 已知一次函数y=x+4的图象经过点（m，6），则m= ．

查看试题解析
13. 如图，菱形ABCD中，∠B＝60°，AB＝3，四边形ACEF是正方形，则EF的长为．

查看试题解析
14. 若甲组数据1，2，3，4，5的方差是S_甲² ，乙组数据6，7，8，9，10的方差是S_乙² ，则S_甲² S_乙²（填“＞”、“＜”或“＝”）

查看试题解析
15. 直线y=﹣2x+b与两坐标轴围成的三角形的面积为1，则b的值为．

查看试题解析
16. 如图，正方形纸片ABCD的边长为12，E，F分别是边AD，BC上的点，将正方形纸片沿EF折叠，使得点A落在CD边上的点A′处，此时点B落在点B′处．已知折痕EF=13，则AE的长等于．

查看试题解析

三、解答题

17. 计算： $\sqrt{18}$ + $\sqrt{8}$ - $\frac{\sqrt{6} \times \sqrt{2}}{\sqrt{3}}$

查看试题解析
18. 已知 x=2- $\sqrt{3}$ ,y=2+ $\sqrt{3}$ ，求代数式x²+2xy+y²的值.

查看试题解析
19. 如图，在平行四边形ABCD中，∠ABD的平分线BE交AD于点E，∠CDB的平分线DF交BC于点F．求证：四边形DEBF是平行四边形．

查看试题解析
20. 如图，已知直线 $l_{1} ： y = x + n - 2$ 与直线 $l_{2} ： y = m x + n$ 相交于点 $P (1 ， 2)$ .

(1)、求 $m$ 、 $n$ 的值；

(2)、请结合图象直接写出不等式 $m x + n > x + n - 2$ 的解集.

查看试题解析
21. 学校开展“书香校园”活动以来，受到同学们的广泛关注，学校为了解全校学生课外阅读的情况，随机调查了部分学生在一周内借阅图书的次数，并制成如图不完整的统计表．学生借阅图书的次数统计表
借阅图书的次数
0次
1次
2次
3次
4次及以上
人数
7
13
a
10
3
请你根据统计图表中的信息，解答下列问题：

(1)、a= ， $b =$ ．

(2)、该调查统计数据的中位数是，众数是．

(3)、请计算扇形统计图中“3次”所对应扇形的圆心角的度数；

(4)、若该校共有2000名学生，根据调查结果，估计该校学生在一周内借阅图书“4次及以上”的人数．

查看试题解析
22. 如图，在四边形ABCD中，∠B＝∠D＝90°，∠C＝60°，AD＝1，BC＝2，求AB、CD的长．

查看试题解析
23. “地摊经济”已成为社会关注的热门话题，小明从市场得知如下信息：

甲商品

乙商品

进价（元/件）

65

5

售价（元/件）

90

10

小明计划购进甲、乙商品共100件进行销售，设小明购进甲商品x件，甲、乙商品全部销售完后获得利润为y元．

(1)、求出y与x之间的函数关系式；

(2)、小明用不超过3500元资金一次性购进甲、乙两种商品，求x的取值范围；

(3)、在（2）的条件下，若要求甲、乙商品全部销售完后获得的利润不少于1250元，请说明当x为何值时利润最大，最大利润是多少？

查看试题解析
24. 如图，已知平面直角坐标系中，A（1，0），C（0，2），现将线段CA绕A点顺时针旋转90°得到点B，连接AB．

(1)、求出直线BC的解析式；

(2)、若动点M从点B出发，沿线段BC以每秒 $\sqrt{10}$ 个单位的速度运动，过点M作MN∥AB交y轴于N，连接AN．设运动时间为t秒，当四边形ABMN为平行四边形时，求t的值；

(3)、P为直线BC上一点，若在坐标平面内存在点Q，使得四边形OBPQ为菱形，请直接写出点Q的坐标．

查看试题解析
25. 如图，已知AD∥BC，AB⊥BC，AB＝BC＝12，P为线段AB上一动点．将△BPC沿PC翻折至△EPC，延长CE交射线AD于点D．

(1)、如图1，当P为AB的中点时，求出AD的长；

(2)、如图2，延长PE交AD于点F，连接CF，求证：∠PCF＝45°；

(3)、如图3，∠MON＝45°，在∠MON内部有一点Q，且OQ＝8，过点Q作OQ的垂线GH分别交OM、ON于G、H两点．当QG＝2时，求QH的值．

查看试题解析

借阅图书的次数	0次	1次	2次	3次	4次及以上
人数	7	13	a	10	3

	甲商品	乙商品
进价（元/件）	65	5
售价（元/件）	90	10