北京市燕山区2020-2021学年八年级下学期数学期末试卷
试卷更新日期:2021-08-16 类型:期末考试
一、单选题
-
1. 若平行四边形中两个内角的度数比为1∶3,则其中较小的内角是( )A、30° B、45° C、60° D、75°2. 计算 ,结果正确的是( )A、 B、 C、 D、3. 已知P1(﹣3,y1),P2(2,y2)是一次函数y=x+1的图象上的两个点,则y1 , y2的大小关系是( )A、y1<y2 B、y1>y2 C、y1=y2 D、不能确定4. 在Rt△ABC中,∠C=90°,AC=3,BC=4,则斜边上的高是( )A、1.2 B、2.4 C、2.5 D、55. 若菱形的两条对角线的长分别为6和10,则菱形的面积为( )A、15 B、24 C、30 D、606. 已知一次函数y=kx+b的图象如图所示,当x≤0时,y的取值范围是( )
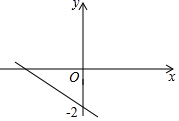 A、y≥0 B、y≤0 C、﹣2≤y<0 D、y≥﹣27. 下列曲线中,表示y是x的函数的是( )A、
A、y≥0 B、y≤0 C、﹣2≤y<0 D、y≥﹣27. 下列曲线中,表示y是x的函数的是( )A、 B、
B、 C、
C、 D、
D、 8. 某校为了解学生的课外阅读情况,随机抽取了一个班级的学生,对他们一周的读书时间进行了统计,统计数据如表所示:
8. 某校为了解学生的课外阅读情况,随机抽取了一个班级的学生,对他们一周的读书时间进行了统计,统计数据如表所示:读书时间(小时)
7
8
9
10
11
学生人数
6
9
10
9
6
关于该班学生一周读书时间的数据有下列说法:①一周读书时间数据的中位数是9小时;②一周读书时间数据的众数是10小时;③一周读书时间数据的平均数是9小时;④一周读书时间不少于9小时的人数占抽查学生的50%.其中说法正确的序号是( )
A、①②③ B、①②④ C、②③④ D、①③9. 想要计算一组数据:197,202,200,201,199,198,203的方差s2 , 在计算平均数的过程中,将这组数据的每一个数都减去200,得到一组新数据﹣3,2,0,1,﹣1,﹣2,3,且新的这组数据的方差为4,则s2为( )A、4 B、16 C、196 D、20410. 周末的早晨王老师从家出发去燕山公园锻炼,她连续、匀速走了60分钟后回到家.如图线段OA﹣AB﹣BC是她出发后所在位置离家的距离s(公里)与行走时间t(分钟)之间的函数关系.则下列图形中可以大致描述王老师行走的路线是( ) A、
A、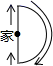 B、
B、 C、
C、 D、
D、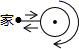
二、填空题
-
11. 若二次根式 有意义,则实数x的取值范围是 .12. 比 大的整数中,最小的是 .13. 在没有直角工具之前,聪明的古埃及人用如图的方法画直角:把一根长绳打上等距离的13个结,然后以3个结间距、4个结间距、5个结间距的长度为边长,用木桩钉成一个三角形,其中5这条边所对的角便是直角.依据是 .
 14. 已知x= ,y= ,则xy= .15. 2022年冬奥会北京赛区,共举办包括滑冰(含短道速滑、速度滑冰、花样滑冰)、冰球、冰壶在内的3个大项5个分项的所有冰上项目比赛,为了迎接2022年的冬奥会,中小学都积极开展冰上运动.小聪和小明进行500米短道速滑训练,他们的五次成绩如表所示:
14. 已知x= ,y= ,则xy= .15. 2022年冬奥会北京赛区,共举办包括滑冰(含短道速滑、速度滑冰、花样滑冰)、冰球、冰壶在内的3个大项5个分项的所有冰上项目比赛,为了迎接2022年的冬奥会,中小学都积极开展冰上运动.小聪和小明进行500米短道速滑训练,他们的五次成绩如表所示:第1次
第2次
第3次
第4次
第5次
小聪
58
53
53
51
60
小明
54
53
56
55
57
设两个人的五次成绩的平均数依次为 小聪 , 小明 , 方差依次为S2小聪 , S2小明 , 你认为两人中技术更好的是,你的理由是 .
16. 把图1中边长为10的菱形沿对角线分成四个全等的直角三角形,且此菱形的一条对角线长为16,将这四个直角三角形拼成如图2所示的正方形,则图2中的阴影的面积为 .
三、解答题
-
17.(1)、化简: ;(2)、计算: .18. 计算: .19. 已知:如图,在▱ABCD中,点M、N分别是AB、CD的中点.求证:DM = BN .
 20. 如图,一块湿地边有两点A,B,点C是与BA方向成直角的AC方向上一点,测得BC=60m,AC=20m.求A,B两点间距离.(结果保留整数)
20. 如图,一块湿地边有两点A,B,点C是与BA方向成直角的AC方向上一点,测得BC=60m,AC=20m.求A,B两点间距离.(结果保留整数) 21. 在坐标系中作出函数y=x+2的图象,根据图象回答下列问题:
21. 在坐标系中作出函数y=x+2的图象,根据图象回答下列问题: (1)、方程x+2=0的解是;(2)、不等式x+2>1的解;(3)、若﹣2≤y≤2,则x的取值范围是 .22. 已知:如图,在△ABC中,AB=AC,D为BC中点,四边形ABDE是平行四边形.
(1)、方程x+2=0的解是;(2)、不等式x+2>1的解;(3)、若﹣2≤y≤2,则x的取值范围是 .22. 已知:如图,在△ABC中,AB=AC,D为BC中点,四边形ABDE是平行四边形.求证:四边形ADCE是矩形.
 23. 已知,直线y=2x+3与直线y=﹣2x﹣1.
23. 已知,直线y=2x+3与直线y=﹣2x﹣1. (1)、求两直线与y轴交点A,B的坐标;(2)、求两直线交点C的坐标;(3)、求△ABC的面积.24. 如图,在菱形ABCD中,AC,BD相交于点O,E为AB的中点,DE⊥AB.
(1)、求两直线与y轴交点A,B的坐标;(2)、求两直线交点C的坐标;(3)、求△ABC的面积.24. 如图,在菱形ABCD中,AC,BD相交于点O,E为AB的中点,DE⊥AB. (1)、求∠DAB和∠CAB的度数;(2)、如果AC=4 ,求DE和AD的长.25. 表格中的两组对应值满足一次函数函数y=kx+b.
(1)、求∠DAB和∠CAB的度数;(2)、如果AC=4 ,求DE和AD的长.25. 表格中的两组对应值满足一次函数函数y=kx+b.1
0
2
(1)、求这个一次函数的解析式;(2)、当x>1时,对于x的每一个值,函数y=mx(m≠0)的值大于一次函数y=kx+b的值,求出m的取值范围.26. 一次函数的图象与x轴、y轴分别交于点A( ,0),B(0,1),以AB为边在第一象限内做等边△ABC. (1)、线段AB的长是 , ∠BAO=°,点C的坐标是;(2)、如果在第二象限内有一点P(a,1),试用含a的代数式表示四边形ABPO的面积.(3)、在y轴上存在点M,使△MAB为等腰三角形,请直接写出点M的坐标.27. 将一块直角三角板的直角顶点和矩形ABCD(AB<BC)的对角线的交点O重合,如图(①→②→③),图中的M、N分别为直角三角形的直角边与矩形ABCD的边CD、BC的交点.
(1)、线段AB的长是 , ∠BAO=°,点C的坐标是;(2)、如果在第二象限内有一点P(a,1),试用含a的代数式表示四边形ABPO的面积.(3)、在y轴上存在点M,使△MAB为等腰三角形,请直接写出点M的坐标.27. 将一块直角三角板的直角顶点和矩形ABCD(AB<BC)的对角线的交点O重合,如图(①→②→③),图中的M、N分别为直角三角形的直角边与矩形ABCD的边CD、BC的交点. (1)、图①(三角板一直角边与OD重合)中,连接DN,则BN与DN的数量关系是 , 进而得到BN,CD,CN的数量关系是;(2)、写出图③(三角板一边与OC重合)中,CN,BN,CD的数量关系是;(3)、试探究图②中BN、CN、CM、DM这四条线段之间的数量关系,写出你的结论,并说明理由.28. 在平面直角坐标系xOy中,对于两点A,B,给出如下定义:以线段AB为边的正方形称为点A,B的“确定正方形”.如图1为点A,B的“确定正方形”的示意图.
(1)、图①(三角板一直角边与OD重合)中,连接DN,则BN与DN的数量关系是 , 进而得到BN,CD,CN的数量关系是;(2)、写出图③(三角板一边与OC重合)中,CN,BN,CD的数量关系是;(3)、试探究图②中BN、CN、CM、DM这四条线段之间的数量关系,写出你的结论,并说明理由.28. 在平面直角坐标系xOy中,对于两点A,B,给出如下定义:以线段AB为边的正方形称为点A,B的“确定正方形”.如图1为点A,B的“确定正方形”的示意图. (1)、如果点C的坐标为(0,1),点D的坐标为(2,1),画出点C,D的一个“确定正方形”,这个正方形的面积是;(2)、已知点O的坐标为(0,0),点M为直线y=x+b(b>0)上一动点,当点O,M的“确定正方形”的面积最小,且最小面积为1时,求b的值.(3)、已知点E在以边长为2的正方形的边上,且该正方形的边与两坐标轴平行,对角线交点为P(m,0),点F在直线y=﹣x﹣2上,若要使所有点E,F的“确定正方形”的面积都不小于2,直接写出m的取值范围.
(1)、如果点C的坐标为(0,1),点D的坐标为(2,1),画出点C,D的一个“确定正方形”,这个正方形的面积是;(2)、已知点O的坐标为(0,0),点M为直线y=x+b(b>0)上一动点,当点O,M的“确定正方形”的面积最小,且最小面积为1时,求b的值.(3)、已知点E在以边长为2的正方形的边上,且该正方形的边与两坐标轴平行,对角线交点为P(m,0),点F在直线y=﹣x﹣2上,若要使所有点E,F的“确定正方形”的面积都不小于2,直接写出m的取值范围.