北京市通州区2020-2021学年八年级下学期数学期末试卷
试卷更新日期:2021-08-16 类型:期末考试
一、单选题
-
1. 方程 的二次项系数和一次项系数分别为( )A、 和 B、 和 C、 和 D、 和2. 下列图形中,既是轴对称图形,又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 在平面直角坐标系 中,过点.轴,垂足为点 ,那么 的长为( )A、2 B、3 C、5 D、4. 方程 的根是A、 B、 C、 , D、 ,5. 甲、乙、丙、丁四名学生参加市中小学生运动会跳高项目预选赛,他们8次跳高的平均成绩及方差如表所示,要选一位成绩较好且稳定的运动员去参赛,应选运动员( )
3. 在平面直角坐标系 中,过点.轴,垂足为点 ,那么 的长为( )A、2 B、3 C、5 D、4. 方程 的根是A、 B、 C、 , D、 ,5. 甲、乙、丙、丁四名学生参加市中小学生运动会跳高项目预选赛,他们8次跳高的平均成绩及方差如表所示,要选一位成绩较好且稳定的运动员去参赛,应选运动员( )甲
乙
丙
丁
(米)
1.72
1.75
1.75
1.72
(米 )
1
1.3
1
1.3
A、甲 B、乙 C、丙 D、丁6. 用配方法解一元二次方程 ,配方变形过程正确的是( )A、 B、 C、 D、7. 如图, 是平行四边形 边 上一点,且 ,连接 ,并延长 与 的延长线交于点 ,如果 ,那么 的度数是( ) A、 B、 C、 D、8. 小明步行从家出发去学校,步行了5分钟时,发现作业忘在家,马上以同样的速度回家取作业,然后骑共享单车赶往学校,小明离家距离S(米)与时间t(分钟)之间的函数图象如图,则小明骑车比步行的速度每分钟快( )
A、 B、 C、 D、8. 小明步行从家出发去学校,步行了5分钟时,发现作业忘在家,马上以同样的速度回家取作业,然后骑共享单车赶往学校,小明离家距离S(米)与时间t(分钟)之间的函数图象如图,则小明骑车比步行的速度每分钟快( ) A、200 B、80 C、140 D、120
A、200 B、80 C、140 D、120二、填空题
-
9. 如图,在象棋棋盘上建立平面直角坐标系,如果使“帅”的位置为点 ,“相”的位置为点 ,那么“炮”的位置为点 .
 10. 通过画出多边形的对角线,可以把多边形内角和问题转化为三角形内角和问题,如果从一个 边形的一个顶点出发最多引出 条对角线,那么这个 边形的内角和是 .11. 如果一元二次方程 的两根分别是 , ,且 ,那么 的值是 .12. 已知 , 是一次函数 的图象上两点,当 时,则 ,那么 的值可以是(写出一个满足题意k的值即可).13. 如果关于 的一元二次方程 的一个解是 ,那么代数式 的值是 .14. 如图,在 中, ,在边 上截取 ,连接 ,过点 作 于点 .已知 , ,如果 是边 的中点,连接 ,那么 的长是 .
10. 通过画出多边形的对角线,可以把多边形内角和问题转化为三角形内角和问题,如果从一个 边形的一个顶点出发最多引出 条对角线,那么这个 边形的内角和是 .11. 如果一元二次方程 的两根分别是 , ,且 ,那么 的值是 .12. 已知 , 是一次函数 的图象上两点,当 时,则 ,那么 的值可以是(写出一个满足题意k的值即可).13. 如果关于 的一元二次方程 的一个解是 ,那么代数式 的值是 .14. 如图,在 中, ,在边 上截取 ,连接 ,过点 作 于点 .已知 , ,如果 是边 的中点,连接 ,那么 的长是 . 15. 在对一组样本数据进行分析时,某同学列出了方的计算公式: ,并由公式得出以下信息:①样本的容量是 ,②样本的中位数是 ,③样本的众数是 ,④样本的平均数是 ,⑤样本的方差是 ,那么上述信息中正确的是(只填序号).16. 《九章算术》是我国古代的数学名著,其中“勾股”章有一题,大意是说:已知矩形门的高比宽多 尺,门的对角线长 尺,那么门的高和宽各是多少?如果设门的宽为 尺,根据题意,那么可列方程 .
15. 在对一组样本数据进行分析时,某同学列出了方的计算公式: ,并由公式得出以下信息:①样本的容量是 ,②样本的中位数是 ,③样本的众数是 ,④样本的平均数是 ,⑤样本的方差是 ,那么上述信息中正确的是(只填序号).16. 《九章算术》是我国古代的数学名著,其中“勾股”章有一题,大意是说:已知矩形门的高比宽多 尺,门的对角线长 尺,那么门的高和宽各是多少?如果设门的宽为 尺,根据题意,那么可列方程 .三、解答题
-
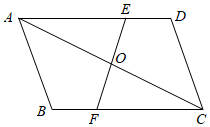
17. 解方程: .18. 如图,在 中,点 , 分别在 、 上,且 ,连接 , 交于点 .求证: .
 19. 已知关于 的一元二次方程 有两个实数根.
19. 已知关于 的一元二次方程 有两个实数根.( )求 的取值范围;
20. 已知一次函数 的图象与 轴交于点 ,与正比例函数 的图象交于点 .( )分别求 , 的值;
21. 已知:在 中, .求作:矩形 .
作法:如下,
①分别以点 , 为圆心,大于 的同样长为半径弧,
两弧分别交于点 , ;
②作直线 ,交边 于点 ;
③作射线 ,以点 为圆心,以 长为半径作弧,与射线 的另一个交点为 ,连接 , ;
所以四边形 就是所求作的矩形.

( )使用直尺和圆规,依作法补全图形(保留作图痕迹):
22. 已知关于 的方程 .( )不解方程,判断方程根的情况,并说明理由;
23. 如图,在 中,对角线 、 相交于点 ,过点 作 交 于 ,如果 , , ,求 的长. 24. 在平面直角坐标系 中,将点 向右平移 个单位长度,得到点 ,点 在直线 上.
24. 在平面直角坐标系 中,将点 向右平移 个单位长度,得到点 ,点 在直线 上.( )求 的值和点 的坐标;
25. 今年7月1日是中国共产党建党 周年纪念日,为了让学生进一步了解中国共产党的历史,某学校组织了一系列“党史知识”专题学习活动,对八年级甲,乙两班各 名学生进行了“党史”相关知识的测试,并分别抽取了 份成绩,并对成绩(百分制并取整数)进行整理、描述和分析,部分信息如下;.甲班、乙班 名学生测试成绩统计如下:(满分 分)
甲班: , , , , , , , , , , , , , , .
乙班: , , , , , , , , , , , , , , .
.甲班 名学生测试成绩的频数分布直方图(不完整):

.乙班 名学生测试成绩的频数分布表:
组别
乙
.甲班、乙班 名学生测试成绩的平均数、众数、中位数和方差如下:
班级
平均数
众数
中位数
方差
甲
乙
根据以上信息,回答下列问题.
(1)、补全甲班测试成绩的频数分布直方图;(2)、在乙班 名学生测试成绩的频数分布表中, , .(3)、在甲班、乙班 名学生测试成绩的平均数、众数、中位数、方差表中, , .(4)、你认为哪个班的学生掌握“党史”相关知识的整体水平较好,说明理由.26. 如图,在平面直角坐标系 中,一次函数 的图象与 轴交于点 ,已知点 , . (1)、求点 的坐标;(2)、直接判断线段 、 的大小关系: (填“>”,“=”或“<”)(3)、如果点 , 到一次函数 图象的距离相等,求 的值.
(1)、求点 的坐标;(2)、直接判断线段 、 的大小关系: (填“>”,“=”或“<”)(3)、如果点 , 到一次函数 图象的距离相等,求 的值.

