安徽省宿州市埇桥区2020-2021学年八年级下学期数学期末试卷

试卷更新日期：2021-08-16 类型：期末考试

进入出卷网下载

一、单选题

1. 下列图形中，既是轴对称图形又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 已知a < b ，则下列选项错误的是（　　）

A、a+2 < b+2 B、a－1 < b－1 C、 $\frac{a}{3} < \frac{b}{3}$ D、－3a <－3b

查看试题解析
3. 下列条件中，不能判定四边形ABCD是平行四边形的是（）

A、AB∥CD，AB＝CD B、AB＝CD，AD＝BC C、AB∥CD，∠B＝∠D D、AB∥CD，AD＝BC

查看试题解析
4. 下列各式从左到右的变形属于因式分解的是（）

A、（x+2）（x-3）=x²-x-6 B、6xy=2x²·3y³ C、x²+2x+1=x（x²+2）+1 D、x²-9=（x-3）（x+3）

查看试题解析
5. 分式 $\frac{2}{2 - x}$ 可变形为（）

A、 $- \frac{2}{x - 2}$ B、 $- \frac{2}{x + 2}$ C、 $- \frac{2}{x - 2}$ D、 $\frac{2}{x + 2}$

查看试题解析
6. 如图， $▱ A B C D$ 的周长为36 cm，对角线 $A C ， B D$ 相交于点 $O ， A C = 12$ cm．若点 $E$ 是 $A B$ 的中点，则 $△ A O E$ 的周长为（）

A、10 cm B、15 cm C、20 cm D、30 cm

查看试题解析
7. 一个多边形的内角和是外角和的2倍，则这个多边形的边数为( )

A、4 B、5 C、6 D、7

查看试题解析
8. 关于x的方程 $\frac{2 x + 3 m}{x - 1} = 1$ 的解是正数，m的值可能是（）

A、 $\frac{2}{3}$ B、 $\frac{1}{2}$ C、0 D、﹣1

查看试题解析
9. “新冠”疫情中，某呼吸机厂家接到一份生产300台呼吸机的订单，在生产完成一半时，应客户要求，需提前供货，每天比原来多生产20台呼吸机，结果提前2天完成任务.设原来每天生产x台呼吸机，下列列出的方程中正确的是（）

A、 $\frac{150}{x} + \frac{150}{x + 20} = \frac{300}{x} + 2$ B、 $\frac{150}{x} + \frac{300}{x + 20} = \frac{300}{x} - 2$ C、 $\frac{150}{x + 20} = \frac{300}{x} - 2$ D、 $\frac{150}{x + 20} = \frac{150}{x} - 2$

查看试题解析
10. 如图，平面直角坐标系中存在点A（3，2），点B（1，0），以线段AB为边作等腰三角形ABP，使得点P在坐标轴上.则这样的P点有（）

A、4个 B、5个 C、6个 D、7个

查看试题解析

二、填空题

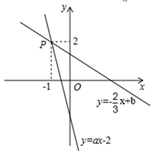
11. 分式 $\frac{x^{2} - 9}{x + 3}$ 的值为0，那么x的值为．

查看试题解析
12. 在 $△$ ABC中，已知∠A＝∠B＝45°，BC＝3，则AB＝．

查看试题解析
13. 如图，已知一次函数y=− $\frac{2}{3}$ x+b和y=ax−2的图象交于点P(−1，2)，则根据图象可得不等式− $\frac{2}{3}$ x+b>ax−2的解集是.

查看试题解析
14. 如图，在平面直角坐标系 $x O y$ 中，有一个等腰直角三角形 $A O B$ ， $∠ O A B = 90 °$ ，直角边 $A O$ 在 $x$ 轴上，且 $A O = 1$ ．将 $Rt Δ AOB$ 绕点 $O$ 顺时针旋转 $90 °$ ，并将两直角边延长，得到等腰直角三角形 $A_{1} O B_{1}$ ，且使 $A_{1} O = 2 A O$ ，再将 $R t$ △ $A_{1} O B_{1}$ 绕点 $O$ 顺时针旋转 $90 °$ ，并将两直角边延长，得到等腰直角三角形 $A_{2} O B_{2}$ ，且使 $A_{2} O = 2 A_{1} O$ ， $\dots$ ，依此规律，得到等腰三角形 $A_{2020} O B_{2020}$ ，则点A₂₀₂₀的坐标为．

查看试题解析

三、解答题

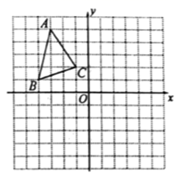
15. 将下列各式因式分解：

(1)、m³n－9mn

(2)、a³＋a－2a²

查看试题解析
16. 解不等式组： ${\begin{array}{l} 3 x + 1 > 2 x \\ \frac{x + 5}{4} - \frac{x}{2} \geq \frac{1}{2} \end{array}$ ，把解集在数轴上表示出来.

查看试题解析
17. 如图，方格纸中每个小正方形的边长都是1个单位长度，在方格纸中建立如图所示的平面直角坐标系．△ABC的顶点都在格点上．

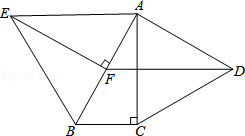
(1)、将△ABC 向右平移 6个单位长度得到△A₁B₁C₁ ，请画出△A₁B₁C₁；

(2)、画出△A₁B₁C₁关于点O的中心对称图形△A₂B₂C₂：

(3)、若将△ABC 绕某一点旋转可得到△A₂B₂C₂ ，请直接写出旋转中心的坐标.

查看试题解析
18. 解方程： $\frac{5}{x - 1} = \frac{3}{x + 3}$ ．

查看试题解析
19. 先化简（1－ $\frac{2 x - 5}{x^{2} - 4}$ ）÷ $\frac{x - 1}{x + 2}$ ，再从0，1，2中选择一个合适的x值代入求值．

查看试题解析
20. 已知(如图)，在四边形ABCD中AB＝CD，过A作AE⊥BD交BD于点E，过C作CF⊥BD交BD于F，且AE＝CF.求证：四边形ABCD是平行四边形.

查看试题解析
21. 开学初，学校要补充部分体育器材，从超市购买了一些排球和篮球．其中购买排球的总价为1000元，购买篮球的总价为1600元，且购买篮球的数量是购买排球数量的2倍．已知购买一个排球比一个篮球贵20元．

种类

标价

优惠方案

A品牌足球

150元/个

八折

B品牌足球

100元/个

九折

(1)、求购买排球和篮球的单价各是多少元；

(2)、为响应“足球进校园”的号召，学校计划再购买50个足球．恰逢另一超市对A、B两种品牌的足球进行降价促销，销售方案如表所示．如果学校此次购买A、B两种品牌足球的总费用不超过5000元．那么最多可购买多少个A品牌足球？

查看试题解析
22. 阅读下列材料，完成相应任务：
神奇的等式

第1个等式： $\frac{1}{2} + \frac{1}{3} + \frac{1}{2 \times 3} = 1$ ；

第2个等式： $\frac{1}{4} + \frac{1}{5} + \frac{1}{4 \times 5} = \frac{1}{2}$ ；

第3个等式： $\frac{1}{6} + \frac{1}{7} + \frac{1}{6 \times 7} = \frac{1}{3}$ ；第4个等式： $\frac{1}{8} + \frac{1}{9} + \frac{1}{8 \times 9} = \frac{1}{4}$ ；…

第100个等式： $\frac{1}{200} + \frac{1}{201} + \frac{1}{200 \times 201} = \frac{1}{100}$ ；…

任务：

(1)、第6个等式为：；

(2)、猜想第n个等式（用含n的代数式表示），并证明．

查看试题解析
23. 如图，分别以Rt△ABC的直角边AC及斜边AB向外作等边△ACD，等边△ABE．已知∠BAC=30°，EF⊥AB，垂足为F，连接DF．

(1)、试说明AC=EF；

(2)、求证：四边形ADFE是平行四边形．

查看试题解析

种类	标价	优惠方案
A品牌足球	150元/个	八折
B品牌足球	100元/个	九折