安徽省铜陵市铜官区2020-2021学年八年级下学期数学期末试卷
试卷更新日期:2021-08-16 类型:期末考试
一、单选题
-
1. 下列式子中,是最简二次根式的是( )A、 B、 C、 D、2. 下列计算正确的是( )A、 B、 C、 D、3. 下列各组数中,以a、b、c为边的三角形不是直角三角形的是( )A、a=1,b= ,c= B、a= ,b=2,c= C、a= ,b= ,c= D、a=7,b=24,c=254. 若一次函数y=(m﹣1)x﹣m的图象经过第二、三、四象限,则m的取值范围是( )A、m<0 B、m<1 C、0<m<1 D、m>15. 下列图象中,表示y是x的函数的是( )A、
 B、
B、 C、
C、 D、
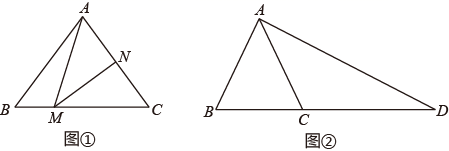
D、 6. 在下列给出的条件中,能判定四边形ABCD为平行四边形的是( )A、AB=BC , CD=DA B、AB//CD , AD=BC C、AB//CD , ∠A=∠C D、∠A=∠B , ∠C=∠D7. 数据按从小到大排列为1,2,4,x,6,9,这组数据的中位数为5,那么这组数据的众数是( )A、4 B、5 C、5.5 D、68. 如图,在▱ABCD中,BF平分∠ABC,交AD于点F,CE平分∠BCD,交AD于点E,若AB=6,EF=2,则BC的长为( )
6. 在下列给出的条件中,能判定四边形ABCD为平行四边形的是( )A、AB=BC , CD=DA B、AB//CD , AD=BC C、AB//CD , ∠A=∠C D、∠A=∠B , ∠C=∠D7. 数据按从小到大排列为1,2,4,x,6,9,这组数据的中位数为5,那么这组数据的众数是( )A、4 B、5 C、5.5 D、68. 如图,在▱ABCD中,BF平分∠ABC,交AD于点F,CE平分∠BCD,交AD于点E,若AB=6,EF=2,则BC的长为( )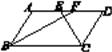 A、8 B、10 C、12 D、149. 小强所在学校离家距离为2千米,某天他放学后骑自行车回家,先骑了5分钟后,因故停留10分钟,再继续骑了5分钟到家.下面哪一个图象能大致描述他回家过程中离家的距离s(千米)与所用时间t(分)之间的关系( )A、
A、8 B、10 C、12 D、149. 小强所在学校离家距离为2千米,某天他放学后骑自行车回家,先骑了5分钟后,因故停留10分钟,再继续骑了5分钟到家.下面哪一个图象能大致描述他回家过程中离家的距离s(千米)与所用时间t(分)之间的关系( )A、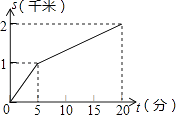 B、
B、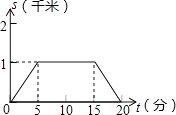 C、
C、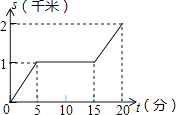 D、
D、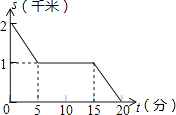 10. 如图,在 , , , ,点P为斜边 上一动点,过点P作 于点 , 于点 ,连结 ,则线段 的最小值为( )
10. 如图,在 , , , ,点P为斜边 上一动点,过点P作 于点 , 于点 ,连结 ,则线段 的最小值为( )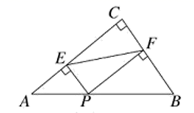 A、1.2 B、2.4 C、2.5 D、4.8
A、1.2 B、2.4 C、2.5 D、4.8二、填空题
-
11. 若二次根式 有意义,则x的取值范围是.12. 若a=2+ ,b=2﹣ ,则ab的值为 .13. 数据﹣2、﹣1、0、1、2的方差是.14. 如图,在△ABC中,∠ACB=90°,M,N分别是AB,AC的中点,延长BC至点D,使CD= BC,连接DM,DN,MN,若AB=6,则DN= .
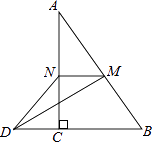 15. 如图,直线 与 轴、 轴分别交于 ,将△ 沿过点 的直线折叠,使点 落 轴正半轴的 点,折痕与 轴交于点 ,则折痕所在直线的解析式为 .
15. 如图,直线 与 轴、 轴分别交于 ,将△ 沿过点 的直线折叠,使点 落 轴正半轴的 点,折痕与 轴交于点 ,则折痕所在直线的解析式为 .
三、解答题
-
16. 计算下列各题:(1)、(2)、17. 如图,网格中的每个小正方形的边长为1,点 均在格点上.
 (1)、直接写出 的长为 , 的面积为;(2)、请在所给的网格中,仅用无刻度的直尺作出 边上的高 ,并保留作图痕迹.18. 在“世界读书日”前夕,某校开展了“让阅读滋养心灵”的读书活动.为了解该校学生在此次活动中的课外阅读情况,从中随机抽取50名学生,调查他们课外阅读书籍的数量,将收集的数据整理成如图所示统计图.
(1)、直接写出 的长为 , 的面积为;(2)、请在所给的网格中,仅用无刻度的直尺作出 边上的高 ,并保留作图痕迹.18. 在“世界读书日”前夕,某校开展了“让阅读滋养心灵”的读书活动.为了解该校学生在此次活动中的课外阅读情况,从中随机抽取50名学生,调查他们课外阅读书籍的数量,将收集的数据整理成如图所示统计图. (1)、求这组数据的平均数;(2)、该校共有800名学生,估计该校全体学生在这次活动中课外阅读书籍的总量大约是多少本?19. 如图,在▱ABCD中,E、F分别为边AB、CD的中点,BD是对角线,AG∥DB交CB的延长线于G .
(1)、求这组数据的平均数;(2)、该校共有800名学生,估计该校全体学生在这次活动中课外阅读书籍的总量大约是多少本?19. 如图,在▱ABCD中,E、F分别为边AB、CD的中点,BD是对角线,AG∥DB交CB的延长线于G . (1)、求证:△ADE≌△CBF;(2)、若四边形AGBD是矩形,则四边形BEDF是什么特殊四边形?请证明你的结论20. 现在“地摊经济”是社会关注的热点话题.小明开展市场调查得到如下信息:
(1)、求证:△ADE≌△CBF;(2)、若四边形AGBD是矩形,则四边形BEDF是什么特殊四边形?请证明你的结论20. 现在“地摊经济”是社会关注的热点话题.小明开展市场调查得到如下信息:小明计划购进甲、乙商品共100件进行摆摊销售.设小明购进甲商品 件,甲、乙商品全部销售完后获得利润为y元.
商品
进价(元/件)
售价(元/件)
甲
35
45
乙
5
8
(1)、求 与 之间的函数关系式:(2)、若小明计划用不超过2000元资金购进甲、乙商品共100件,求 的取值范围;(3)、在(2)的条件下,若甲、乙商品全部销售完后获得的利润 不少于632.5元,那么小明有哪几种进货方案?哪种进货方案获得的利润最大?