福建省近5年中考数学真题分类卷5 图形的变换
试卷更新日期:2021-08-16 类型:二轮复习
一、单选题
-
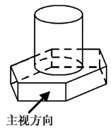
1. 如图所示的六角螺栓,其俯视图是( )
 A、
A、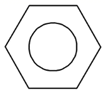 B、
B、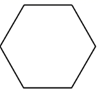 C、
C、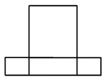 D、
D、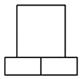 2. 如图,由四个正方体组成的几何体的左视图是( )
2. 如图,由四个正方体组成的几何体的左视图是( )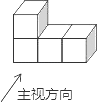 A、
A、 B、
B、 C、
C、 D、
D、 3. 如图,某研究性学习小组为测量学校A与河对岸工厂B之间的距离,在学校附近选一点C,利用测量仪器测得 .据此,可求得学校与工厂之间的距离 等于( )
3. 如图,某研究性学习小组为测量学校A与河对岸工厂B之间的距离,在学校附近选一点C,利用测量仪器测得 .据此,可求得学校与工厂之间的距离 等于( )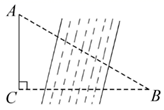 A、 B、 C、 D、4. 如图, 是等腰三角形 的顶角平分线, ,则 等于( )
A、 B、 C、 D、4. 如图, 是等腰三角形 的顶角平分线, ,则 等于( )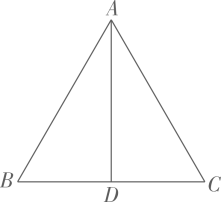 A、10 B、5 C、4 D、35. 下列给出的等边三角形、平行四边形、圆及扇形中,既是轴对称图形又是中心对称图形的是( )A、
A、10 B、5 C、4 D、35. 下列给出的等边三角形、平行四边形、圆及扇形中,既是轴对称图形又是中心对称图形的是( )A、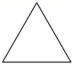 B、
B、 C、
C、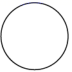 D、
D、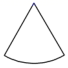 6. 如图所示的六角螺母,其俯视图是( )
6. 如图所示的六角螺母,其俯视图是( )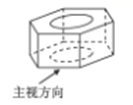 A、
A、 B、
B、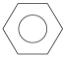 C、
C、 D、
D、 7. 下列图形中,一定既是轴对称图形又是中心对称图形的是( ).A、等边三角形 B、直角三角形 C、平行四边形 D、正方形8. 如图是由一个长方体和一个球组成的几何体,它的主视图是( ).
7. 下列图形中,一定既是轴对称图形又是中心对称图形的是( ).A、等边三角形 B、直角三角形 C、平行四边形 D、正方形8. 如图是由一个长方体和一个球组成的几何体,它的主视图是( ).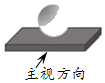 A、
A、 B、
B、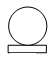 C、
C、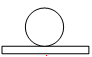 D、
D、 9. 某几何体的三视图如图所示,则该几何体是( )
9. 某几何体的三视图如图所示,则该几何体是( ) A、圆柱 B、三棱柱 C、长方体 D、四棱锥10. 如图,网格纸上正方形小格的边长为1.图中线段AB和点P绕着同一个点做相同的旋转,分别得到线段A'B'和点P',则点P'所在的单位正方形区域是( )
A、圆柱 B、三棱柱 C、长方体 D、四棱锥10. 如图,网格纸上正方形小格的边长为1.图中线段AB和点P绕着同一个点做相同的旋转,分别得到线段A'B'和点P',则点P'所在的单位正方形区域是( )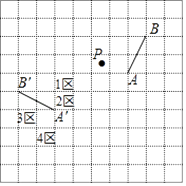 A、1区 B、2区 C、3区 D、4区
A、1区 B、2区 C、3区 D、4区二、填空题
-
11. 如图,数轴上A、B两点所表示的数分别是-4和2, 点C是线段AB的中点,则点C所表示的数是.
 12. 把两个同样大小的含45°角的三角尺按如图所示的方式放置,其中一个三角尺的锐角顶点与另一个的直角顶点重合于点A,且另三个锐角顶点B,C,D在同一直线上.若AB= ,则CD= .
12. 把两个同样大小的含45°角的三角尺按如图所示的方式放置,其中一个三角尺的锐角顶点与另一个的直角顶点重合于点A,且另三个锐角顶点B,C,D在同一直线上.若AB= ,则CD= .
三、综合题
-
13. 如图,在 中, .线段 是由线段 平移得到的,点F在边 上, 是以 为斜边的等腰直角三角形,且点D恰好在 的延长线上.
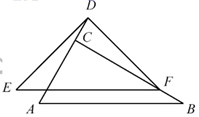 (1)、求证: ;(2)、求证: .14. 如图,在正方形 中,E,F为边 上的两个三等分点,点A关于 的对称点为 , 的延长线交 于点G.
(1)、求证: ;(2)、求证: .14. 如图,在正方形 中,E,F为边 上的两个三等分点,点A关于 的对称点为 , 的延长线交 于点G.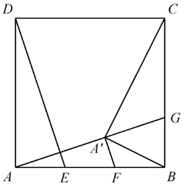 (1)、求证: ;(2)、求 的大小;(3)、求证: .15. 如图, 由 绕点 按逆时针方向旋转 得到,且点 的对应点D恰好落在 的延长线上, , 相交于点 .
(1)、求证: ;(2)、求 的大小;(3)、求证: .15. 如图, 由 绕点 按逆时针方向旋转 得到,且点 的对应点D恰好落在 的延长线上, , 相交于点 . (1)、求 的度数;(2)、 是 延长线上的点,且 .
(1)、求 的度数;(2)、 是 延长线上的点,且 .①判断 和 的数量关系,并证明;
②求证: .
16. 如图,已知△ABC为和点A'. (1)、以点A'为顶点求作△A'B'C' , 使△A'B'C'∽△ABC , S△A'B'C'=4S△ABC;
(1)、以点A'为顶点求作△A'B'C' , 使△A'B'C'∽△ABC , S△A'B'C'=4S△ABC;(尺规作图,保留作图痕迹,不写作法)
(2)、设D、E、F分别是△ABC三边AB、BC、AC的中点,D'、E'、F'分别是你所作的△A'B'C'三边A'B'、B'C'、A'C'的中点,求证:△DEF∽△D'E'F'.17. 在Rt△ABC中,∠ABC=90°,∠BAC=30°,将△ABC绕点A顺时针旋转一定的角度 得到△AED , 点B、C的对应点分别是E、D.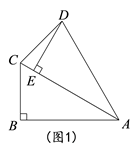
 (1)、如图1,当点E恰好在AC上时,求∠CDE的度数;(2)、如图2,若 =60°时,点F是边AC中点,求证:四边形BFDE是平行四边形.18. 如图,在Rt△ABC中,∠C=90°,AB=10,AC=8.线段AD由线段AB绕点A按逆时针方向旋转90°得到,△EFG由△ABC沿CB方向平移得到,且直线EF过点D.
(1)、如图1,当点E恰好在AC上时,求∠CDE的度数;(2)、如图2,若 =60°时,点F是边AC中点,求证:四边形BFDE是平行四边形.18. 如图,在Rt△ABC中,∠C=90°,AB=10,AC=8.线段AD由线段AB绕点A按逆时针方向旋转90°得到,△EFG由△ABC沿CB方向平移得到,且直线EF过点D. (1)、求∠BDF的大小;(2)、求CG的长.19. 已知四边形ABCD是⊙O的内接四边形,AC是⊙O的直径,DE⊥AB,垂足为E.
(1)、求∠BDF的大小;(2)、求CG的长.19. 已知四边形ABCD是⊙O的内接四边形,AC是⊙O的直径,DE⊥AB,垂足为E.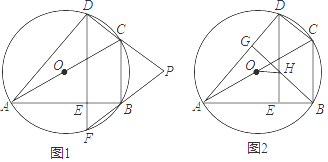 (1)、延长DE交⊙O于点F,延长DC,FB交于点P,如图1.求证:PC=PB;(2)、过点B作BC⊥AD,垂足为G,BG交DE于点H,且点O和点A都在DE的左侧,如图2.若AB= ,DH=1,∠OHD=80°,求∠BDE的大小.20. 如图,D是△ABC外接圆上的动点,且B,D位于AC的两侧,DE⊥AB,垂足为E,DE的延长线交此圆于点F.BG⊥AD,垂足为G,BG交DE于点H,DC,FB的延长线交于点P,且PC=PB.
(1)、延长DE交⊙O于点F,延长DC,FB交于点P,如图1.求证:PC=PB;(2)、过点B作BC⊥AD,垂足为G,BG交DE于点H,且点O和点A都在DE的左侧,如图2.若AB= ,DH=1,∠OHD=80°,求∠BDE的大小.20. 如图,D是△ABC外接圆上的动点,且B,D位于AC的两侧,DE⊥AB,垂足为E,DE的延长线交此圆于点F.BG⊥AD,垂足为G,BG交DE于点H,DC,FB的延长线交于点P,且PC=PB.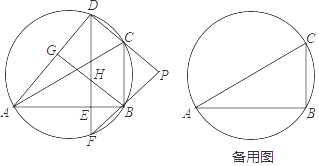 (1)、求证:BG∥CD;(2)、设△ABC外接圆的圆心为O,若AB= DH,∠OHD=80°,求∠BDE的大小.21. 求证:相似三角形对应边上的中线之比等于相似比.
(1)、求证:BG∥CD;(2)、设△ABC外接圆的圆心为O,若AB= DH,∠OHD=80°,求∠BDE的大小.21. 求证:相似三角形对应边上的中线之比等于相似比.要求:①根据给出的△ABC及线段A'B′,∠A′(∠A′=∠A),以线段A′B′为一边,在给出的图形上用尺规作出△A'B′C′,使得△A'B′C′∽△ABC,不写作法,保留作图痕迹;
②在已有的图形上画出一组对应中线,并据此写出已知、求证和证明过程.
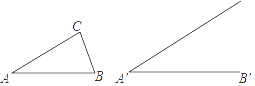 22. 小明在某次作业中得到如下结果:
22. 小明在某次作业中得到如下结果:sin27°+sin283°≈0.122+0.992=0.9945,
sin222°+sin268°≈0.372+0.932=1.0018,
sin229°+sin261°≈0.482+0.872=0.9873,
sin237°+sin253°≈0.602+0.802=1.0000,
sin245°+sin245°≈( )2+( )2=1.
据此,小明猜想:对于任意锐角α,均有sin2α+sin2(90°﹣α)=1.
(Ⅰ)当α=30°时,验证sin2α+sin2(90°﹣α)=1是否成立;
(Ⅱ)小明的猜想是否成立?若成立,请给予证明;若不成立,请举出一个反例.
23. 如图,矩形ABCD中,AB=6,AD=8,P,E分别是线段AC、BC上的点,且四边形PEFD为矩形.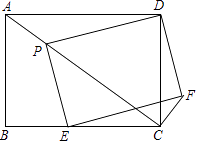
(Ⅰ)若△PCD是等腰三角形时,求AP的长;
(Ⅱ)若AP= ,求CF的长.