福建省近5年中考数学真题分类卷4-图形的性质
试卷更新日期:2021-08-16 类型:二轮复习
一、单选题
-
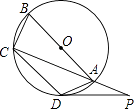
1. 如图, 为 的直径,点P在 的延长线上, 与 相切,切点分别为C,D.若 ,则 等于( )
 A、 B、 C、 D、2. 如图,点F在正五边形 的内部, 为等边三角形,则 等于( )
A、 B、 C、 D、2. 如图,点F在正五边形 的内部, 为等边三角形,则 等于( )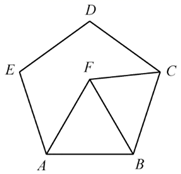 A、 B、 C、 D、3. 如图,四边形 内接于 , , 为 中点, ,则 等于( )
A、 B、 C、 D、3. 如图,四边形 内接于 , , 为 中点, ,则 等于( )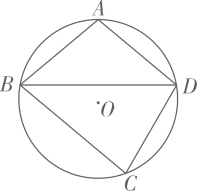 A、 B、 C、 D、4. 如图,面积为1的等边三角形 中, 分别是 , , 的中点,则 的面积是( )
A、 B、 C、 D、4. 如图,面积为1的等边三角形 中, 分别是 , , 的中点,则 的面积是( ) A、1 B、 C、 D、5. 如图,PA、PB是⊙O切线,A、B为切点,点C在⊙O上,且∠ACB=55°,则∠APB等于( )
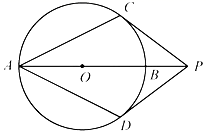
A、1 B、 C、 D、5. 如图,PA、PB是⊙O切线,A、B为切点,点C在⊙O上,且∠ACB=55°,则∠APB等于( )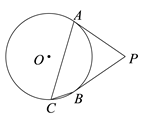 A、55° B、70° C、110° D、125°6. 已知正多边形的一个外角为36°,则该正多边形的边数为( ).A、12 B、10 C、8 D、67. 如图,等边三角形ABC中,AD⊥BC,垂足为D,点E在线段AD上,∠EBC=45°,则∠ACE等于( )
A、55° B、70° C、110° D、125°6. 已知正多边形的一个外角为36°,则该正多边形的边数为( ).A、12 B、10 C、8 D、67. 如图,等边三角形ABC中,AD⊥BC,垂足为D,点E在线段AD上,∠EBC=45°,则∠ACE等于( )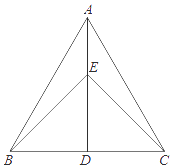 A、15° B、30° C、45° D、60°8. 如图,AB是⊙O的直径,BC与⊙O相切于点B,AC交⊙O于点D,若∠ACB=50°,则∠BOD等于( )
A、15° B、30° C、45° D、60°8. 如图,AB是⊙O的直径,BC与⊙O相切于点B,AC交⊙O于点D,若∠ACB=50°,则∠BOD等于( ) A、40° B、50° C、60° D、80°9. 一个n边形的内角和为360°,则n等于( )
A、40° B、50° C、60° D、80°9. 一个n边形的内角和为360°,则n等于( )
A、3 B、4 C、5 D、610. 下列各组数中,能作为一个三角形三边边长的是( )
A、1,1,2 B、1,2,4 C、2,3,4 D、2,3,511. 如图,AB是⊙O的直径,C,D是⊙O上位于AB异侧的两点.下列四个角中,一定与∠ACD互余的角是( )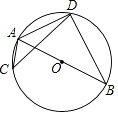 A、∠ADC B、∠ABD C、∠BAC D、∠BAD12. 下列关于图形对称性的命题,正确的是( )A、圆既是轴对称性图形,又是中心对称图形 B、正三角形既是轴对称图形,又是中心对称图形 C、线段是轴对称图形,但不是中心对称图形 D、菱形是中心对称图形,但不是轴对称图形
A、∠ADC B、∠ABD C、∠BAC D、∠BAD12. 下列关于图形对称性的命题,正确的是( )A、圆既是轴对称性图形,又是中心对称图形 B、正三角形既是轴对称图形,又是中心对称图形 C、线段是轴对称图形,但不是中心对称图形 D、菱形是中心对称图形,但不是轴对称图形二、填空题
-
13. 如图,在矩形 中, ,点E,F分别是边 上的动点,点E不与A,B重合,且 ,G是五边形 内满足 且 的点.现给出以下结论:
① 与 一定互补;
②点G到边 的距离一定相等;
③点G到边 的距离可能相等;
④点G到边 的距离的最大值为 .
其中正确的是.(写出所有正确结论的序号)
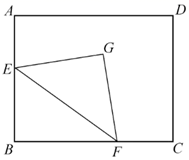 14. 如图, 是 的角平分线.若 ,则点D到 的距离是.
14. 如图, 是 的角平分线.若 ,则点D到 的距离是. 15. 一个扇形的圆心角是 ,半径为4,则这个扇形的面积为 . (结果保留 )16. 如图所示的六边形花环是用六个全等的直角三角形拼成的,则 等于度.
15. 一个扇形的圆心角是 ,半径为4,则这个扇形的面积为 . (结果保留 )16. 如图所示的六边形花环是用六个全等的直角三角形拼成的,则 等于度.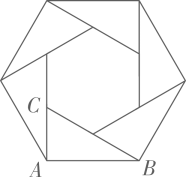 17. 在平面直角坐标系xOy中,▱OABC的三个顶点O(0,0)、A(3,0) 、 B(4,2),则其第四个顶点是.18. 如图,边长为2的正方形ABCD中心与半径为2的⊙O的圆心重合,E、F分别是AD、BA的延长与⊙O的交点,则图中阴影部分的面积是.(结果保留 )
17. 在平面直角坐标系xOy中,▱OABC的三个顶点O(0,0)、A(3,0) 、 B(4,2),则其第四个顶点是.18. 如图,边长为2的正方形ABCD中心与半径为2的⊙O的圆心重合,E、F分别是AD、BA的延长与⊙O的交点,则图中阴影部分的面积是.(结果保留 ) 19. 如图,Rt△ABC中,∠ACB=90°,AB=6,D是AB的中点,则CD= .
19. 如图,Rt△ABC中,∠ACB=90°,AB=6,D是AB的中点,则CD= .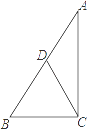 20. 如图,Rt△ABC中,∠ACB=90°,AB=6,D是AB的中点,则CD= .
20. 如图,Rt△ABC中,∠ACB=90°,AB=6,D是AB的中点,则CD= . 21. 两个完全相同的正五边形都有一边在直线l上,且有一个公共顶点O,其摆放方式如图所示,则∠AOB等于度.
21. 两个完全相同的正五边形都有一边在直线l上,且有一个公共顶点O,其摆放方式如图所示,则∠AOB等于度. 22. 如图,△ABC中,D,E分别是AB,AC的中点,连线DE.若DE=3,则线段BC的长等于 .
22. 如图,△ABC中,D,E分别是AB,AC的中点,连线DE.若DE=3,则线段BC的长等于 .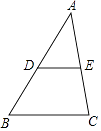
三、解答题
-
23. 如图,在 中,D是边 上的点, ,垂足分别为E,F,且 .求证: .
 24. 如图,点E、F分别在菱形 的边 , 上,且 .
24. 如图,点E、F分别在菱形 的边 , 上,且 .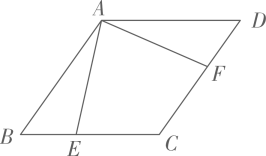
求证: .
25. 如图,点E、F分别是矩形ABCD的边 AB、CD上的一点,且DF=BE.求证:AF=CE.
 26. 如图,▱ABCD的对角线AC,BD相交于点O,EF过点O且与AD,BC分别相交于点E,F.求证:OE=OF.
26. 如图,▱ABCD的对角线AC,BD相交于点O,EF过点O且与AD,BC分别相交于点E,F.求证:OE=OF. 27. 如图,点B、E、C、F在同一直线上,AB=DE,AC=DF,BE=CF.求证:∠A=∠D.
27. 如图,点B、E、C、F在同一直线上,AB=DE,AC=DF,BE=CF.求证:∠A=∠D.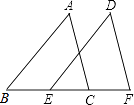
四、作图题
-
28. 如图,C为线段 外一点.
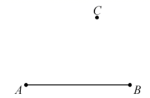 (1)、求作四边形 ,使得 ,且 ;(要求:尺规作图,不写作法,保留作图痕迹)(2)、在(1)的四边形 中, , 相交于点P, , 的中点分别为 ,求证: 三点在同一条直线上.29. 如图,△ABC中,∠BAC=90°,AD⊥BC,垂足为D.求作∠ABC的平分线,分别交AD,AC于P,Q两点;并证明AP=AQ.(要求:尺规作图,保留作图痕迹,不写作法)
(1)、求作四边形 ,使得 ,且 ;(要求:尺规作图,不写作法,保留作图痕迹)(2)、在(1)的四边形 中, , 相交于点P, , 的中点分别为 ,求证: 三点在同一条直线上.29. 如图,△ABC中,∠BAC=90°,AD⊥BC,垂足为D.求作∠ABC的平分线,分别交AD,AC于P,Q两点;并证明AP=AQ.(要求:尺规作图,保留作图痕迹,不写作法)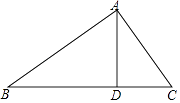 30. 如图,已知线段 ,垂足为a.
30. 如图,已知线段 ,垂足为a.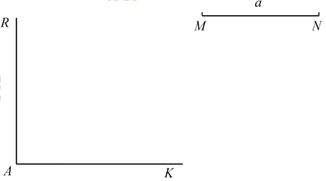 (1)、求作四边形 ,使得点B,D分别在射线 上,且 , , ;(要求:尺规作图,不写作法,保留作图痕迹)(2)、设P,Q分别为(1)中四边形 的边 的中点,求证:直线 相交于同一点.
(1)、求作四边形 ,使得点B,D分别在射线 上,且 , , ;(要求:尺规作图,不写作法,保留作图痕迹)(2)、设P,Q分别为(1)中四边形 的边 的中点,求证:直线 相交于同一点.五、综合题
-
31. 如图,四边形ABCD内接于⊙O , AB=AC , BD⊥AC , 垂足为E , 点F在BD的延长线上,且DF=DC , 连接AF、CF.
 (1)、求证:∠BAC=2∠DAC;(2)、若AF=10,BC=4 ,求tan∠BAD的值.
(1)、求证:∠BAC=2∠DAC;(2)、若AF=10,BC=4 ,求tan∠BAD的值.