福建省近5年中考数学真题分类卷3-函数综合

试卷更新日期：2021-08-16 类型：二轮复习

进入出卷网下载

一、单选题

1. 如图，一次函数 $y = k x + b (k > 0)$ 的图象过点 $(- 1 ， 0)$ ，则不等式 $k (x - 1) + b > 0$ 的解集是（）

A、 $x > - 2$ B、 $x > - 1$ C、 $x > 0$ D、 $x > 1$

查看试题解析
2. 二次函数 $y = a x^{2} - 2 a x + c (a > 0)$ 的图象过 $A (- 3 ， y_{1}) ， B (- 1 ， y_{2}) ， C (2 ， y_{3}) ， D (4 ， y_{4})$ 四个点，下列说法一定正确的是（）

A、若 $y_{1} y_{2} > 0$ ，则 $y_{3} y_{4} > 0$ B、若 $y_{1} y_{4} > 0$ ，则 $y_{2} y_{3} > 0$ C、若 $y_{2} y_{4} < 0$ ，则 $y_{1} y_{3} < 0$ D、若 $y_{3} y_{4} < 0$ ，则 $y_{1} y_{2} < 0$

查看试题解析
3. 若二次函数y=|a|x²+bx+c的图象经过A(m ， n)、B(0，y₁)、C(3－m ， n)、D( $\sqrt{2}$ ， y₂)、E(2，y₃)，则y₁、y₂、y₃的大小关系是（）.

A、y₁< y₂< y₃ B、y₁ < y₃< y₂ C、y₃< y₂< y₁ D、y₂< y₃< y₁

查看试题解析
4. 若直线y=kx+k+1经过点（m，n+3）和（m+1，2n﹣1），且0＜k＜2，则n的值可以是（）

A、3 B、4 C、5 D、6

查看试题解析
5. 已知 $P_{1} (x_{1} ， y_{1})$ ， $P_{2} (x_{2} ， y_{2})$ 是抛物线 $y = a x^{2} - 2 a x$ 上的点，下列命题正确的是（）

A、若 $| x_{1} - 1 | > | x_{2} - 1 |$ ，则 $y_{1} > y_{2}$ B、若 $| x_{1} - 1 | > | x_{2} - 1 |$ ，则 $y_{1} < y_{2}$ C、若 $| x_{1} - 1 | = | x_{2} - 1 |$ ，则 $y_{1} = y_{2}$ D、若 $y_{1} = y_{2}$ ，则 $x_{1} = x_{2}$

查看试题解析

二、填空题

6. 若反比例函数 $y = \frac{k}{x}$ 的图象过点 $(1 ， 1)$ ，则k的值等于.

查看试题解析
7. 已知矩形ABCD的四个顶点均在反比例函数y= $\frac{1}{x}$ 的图象上，且点A的横坐标是2，则矩形ABCD的面积为．

查看试题解析
8. 如图，直线y=x+m与双曲线y= $\frac{3}{x}$ 相交于A，B两点，BC∥x轴，AC∥y轴，则△ABC面积的最小值为．

查看试题解析
9. 如图，菱形ABCD顶点A在例函数y= $\frac{3}{x}$ (x>0)的图象上，函数 y= $\frac{k}{x}$ (k>3，x>0)的图象关于直线AC对称，且经过点B、D两点，若AB＝2，∠DAB＝30°，则k的值为.

查看试题解析

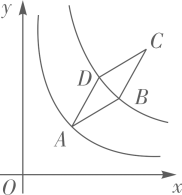
三、综合题

10. 某公司经营某种农产品，零售一箱该农产品的利润是70元，批发一箱该农产品的利润是40元.

(1)、已知该公司某月卖出100箱这种农产品共获利润4600元，问：该公司当月零售、批发这种农产品的箱数分别是多少？

(2)、经营性质规定，该公司零售的数量不能多于总数量的30%.现该公司要经营1000箱这种农产品，问：应如何规划零售和批发的数量，才能使总利润最大？最大总利润是多少？

查看试题解析
11. 某公司经营甲、乙两种特产，其中甲特产每吨成本价为10万元，销售价为10.5万元；乙特产每吨成本价为1万元，销售价为1.2万元．由于受有关条件限制，该公司每月这两种特产的销售量之和都是100吨，且甲特产的销售量都不超过20吨．

(1)、若该公司某月销售甲、乙两种特产的总成本为235万元，问这个月该公司分别销售甲、乙两种特产各多少吨？

(2)、求该公司一个月销售这两种特产所能获得的最大总利润．

查看试题解析
12. 空地上有一段长为a米的旧墙MN，某人利用旧墙和木栏围成一个矩形菜园ABCD，已知木栏总长为100米．

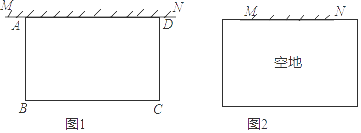(1)、已知a=20，矩形菜园的一边靠墙，另三边一共用了100米木栏，且围成的矩形菜园面积为450平方米．
如图1，求所利用旧墙AD的长；

(2)、已知0＜α＜50，且空地足够大，如图2．请你合理利用旧墙及所给木栏设计一个方案，使得所围成的矩形菜园ABCD的面积最大，并求面积的最大值．

查看试题解析
13. 已知抛物y=ax²+bx+c(b<0)与轴只有一个公共点.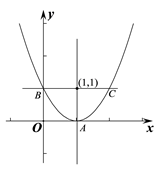

(1)、若公共点坐标为(2，0)，求a、c满足的关系式；

(2)、设A为抛物线上的一定点，直线l：y=kx+1－k与抛物线交于点B、C两点，直线BD垂直于直线y=－1，垂足为点D.当k＝0时，直线l与抛物线的一个交点在 y轴上，且△ABC为等腰直角三角形.
①求点A的坐标和抛物线的解析式；

②证明：对于每个给定的实数 k ，都有A、D、C三点共线.

查看试题解析
14. 已知抛物线y=ax²+bx+c过点A（0，2）．

(1)、若点（﹣ $\sqrt{2}$ ，0）也在该抛物线上，求a，b满足的关系式；

(2)、若该抛物线上任意不同两点M（x₁ ， y₁），N（x₂ ， y₂）都满足：当x₁＜x₂＜0时，（x₁﹣x₂）（y₁﹣y₂）＞0；当0＜x₁＜x₂时，（x₁﹣x₂）（y₁﹣y₂）＜0．以原点O为心，OA为半径的圆与拋物线的另两个交点为B，C，且△ABC有一个内角为60°．
①求抛物线的解析式；
②若点P与点O关于点A对称，且O，M，N三点共线，求证：PA平分∠MPN．

查看试题解析
15. 已知直线 $l_{1} ： y = - 2 x + 10$ 交y轴于点A，交 $x$ 轴于点B，二次函数的图象过 $A ， B$ 两点，交x轴于另一点 $C$ ， $B C = 4$ ，且对于该二次函数图象上的任意两点 $P_{1} (x_{1} ， y_{1})$ ， $P_{2} (x_{2} ， y_{2})$ ，当 $x_{1} > x_{2} \geq 5$ 时，总有 $y_{1} > y_{2}$ ．

(1)、求二次函数的表达式；

(2)、若直线 $l_{2} ： y = m x + n (n \neq 10)$ ，求证：当 $m = - 2$ 时， $l_{2} / / l_{1}$ ；

(3)、E为线段 $B C$ 上不与端点重合的点，直线 $l_{3} ： y = - 2 x + q$ 过点C且交直线 $A E$ 于点F，求 $Δ A B E$ 与 $Δ C E F$ 面积之和的最小值．

查看试题解析
16. 已知抛物线y=ax²+bx+c过点A（0，2），且抛物线上任意不同两点M（x₁ ， y₁），N（x₂ ， y₂）都满足：当x₁＜x₂＜0时，（x₁﹣x₂）（y₁﹣y₂）＞0；当0＜x₁＜x₂时，（x₁﹣x₂）（y₁﹣y₂）＜0．以原点O为圆心，OA为半径的圆与抛物线的另两个交点为B，C，且B在C的左侧，△ABC有一个内角为60°．

(1)、求抛物线的解析式；

(2)、若MN与直线y=﹣2 $\sqrt{3}$ x平行，且M，N位于直线BC的两侧，y₁＞y₂ ，解决以下问题：
①求证：BC平分∠MBN；
②求△MBC外心的纵坐标的取值范围．

查看试题解析
17. 已知抛物线 $y = a x^{2} + b x + c$ 与x轴只有一个公共点.

(1)、若抛物线过点 $P (0 ， 1)$ ，求 $a + b$ 的最小值；

(2)、已知点 $P_{1} (- 2 ， 1) ， P_{2} (2 ， - 1) ， P_{3} (2 ， 1)$ 中恰有两点在抛物线上.
①求抛物线的解析式；

②设直线l： $y = k x + 1$ 与抛物线交于M，N两点，点A在直线 $y = - 1$ 上，且 $∠ M A N = 90 °$ ，过点A且与x轴垂直的直线分别交抛物线和于点B，C.求证： $△ M A B$ 与 $△ M B C$ 的面积相等.

查看试题解析