初中数学浙教版七年级上册4.2 代数式同步练习

试卷更新日期：2021-08-16 类型：同步测试

进入出卷网下载

一、单选题

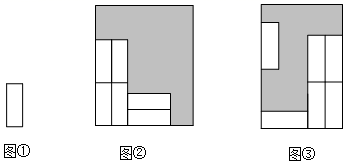
1. 某地居民生活用水收费标准：每月用水量不超过17立方米，每立方米 $a$ 元；超过部分每立方米 $(a + 1.2)$ 元.该地区某用户上月用水量为20立方米，则应缴水费为（）

A、 $20 a$ 元 B、 $(20 a + 24)$ 元 C、 $(17 a + 3.6)$ 元 D、 $(20 a + 3.6)$ 元

查看试题解析
2. 某超市出售一商品，有如下四种在原标价基础上调价的方案，其中调价后售价最低的是（）

A、先打九五折，再打九五折 B、先提价 $50 %$ ，再打六折 C、先提价 $30 %$ ，再降价 $30 %$ D、先提价 $25 %$ ，再降价 $25 %$

查看试题解析
3. 把六张形状大小完全相同的小长方形卡片（如图①），分两种不同形式不重叠的放在一个长方形盒子底部（如图②、图③），盒子底面未被卡片覆盖的部分用阴影表示，设图②是长方形盒子的周长为C₁ ，阴影部分图形的周长为l₁ ，图③中长方形盒子的周长为C₂ ，阴影部分图形的周长为l₂ ，若C₁﹣C₂＝2，则l₁ ， l₂满足（）

A、l₁＝l₂ B、l₁﹣l₂＝1 C、l₁﹣l₂＝2 D、l₁﹣l₂＝4

查看试题解析
4. 《九章算术》中记载一问题：今有共买物，人出八，盈三；人出七，不足四，问人数、物价各几何?意思是：今有人合伙购物，每人出8钱，会多3钱；每人出7钱，又差4钱。问人数、物价各多少?设有x人，则表示物价的代数式可以是（）

A、8x-3 B、8x+3 C、7x-4 D、7(x+4)

查看试题解析
5. 小颖用4张长为a，宽为b（a＞b）的长方形纸片，按如图的方式拼成一个边长为（a+b）的正方形，图中空白部分的面积为S₁ ，阴影部分的面积为S₂ ．若a＝2b，则S₁ ， S₂之间的数量关系为（）

A、S₁＝ $\frac{3}{2}$ S₂ B、S₁＝2S₂ C、S₁＝ $\frac{5}{2}$ S₂ D、S₁＝3S₂

查看试题解析
6. 我们已经接触了很多代数恒等式，知道可以用一些硬纸片拼成的图形的面积来解释一些代数恒等式．例如图1可以用来解释 ${(a + b)}^{2} - {(a - b)}^{2} = 4 a b$ ．那么通过图2中阴影部分面积的计算验证的恒等式是：（）

A、 ${(a - b)}^{2} = a^{2} - 2 a b + b^{2}$ B、 $a^{2} - b^{2} = (a + b) (a - b)$ C、 ${(a + b)}^{2} = a^{2} + 2 a b + b^{2}$ D、 $(a - b) (a + 2 b) = a^{2} + a b - 2 b^{2}$

查看试题解析
7. 某汽车的油箱一次加满汽油50升，可行驶y千米（假设汽油能行驶至油用完），设该汽车行驶每100千米耗油x升，则y关于x的函数表达式为（）

A、 $y = 2 x$ B、 $y = \frac{2}{x}$ C、 $y = 5000 x$ D、 $y = \frac{5000}{x}$

查看试题解析
8. 甲、乙两个油桶中装有体积相等的油.先把甲桶的油倒一半到乙桶（乙桶没有溢出），再把乙桶的油倒出 $\frac{1}{3}$ 给甲桶（甲桶没有溢出），这时两个油桶中的油的是（　　）

A、甲桶的油多 B、乙桶的油多 C、甲桶与乙桶一样多 D、无法判断，与原有的油的体积大小有关

查看试题解析
9. “五水共治”工程中，要挖掘一段a千米的排污管沟，如果由10个工人挖掘，要用m天完成；如果由一台挖掘机工作，要比10个工人挖掘提前3天完成，一台挖掘机的工作效率是一个工人工作效率的（）

A、 $\frac{a}{m - 3}$ B、 $\frac{a}{7 m}$ C、 $\frac{10 m}{m - 3}$ D、 $\frac{m - 3}{10 m}$

查看试题解析
10. 某校组织若干师生进行社会实践活动.若学校租用 $45$ 座的客车x辆，则余下 $15$ 人无座位；若租用 $60$ 座的客车则可少租用 $1$ 辆，则最后一辆还没坐满，那么乘坐最后一辆 $60$ 座客车的人数是（）

A、75-15x B、135-15x C、75+15x D、135-60x

查看试题解析

二、填空题

11. 一本笔记本的原价是1n元，现在按8折出售，购买5本笔记本需要付费元

查看试题解析
12. 一个长方形花园，长为a ，宽为b ，中间有两条互相垂直的宽为c的路，则可种花的面积为．

查看试题解析
13. 夏季荷花盛开，为了便于游客领略“人从桥上过，如在河中行”的美好意境，某景点拟在如图所示的长方形荷塘上架设小桥.若荷塘周长为280m，且桥宽忽略不计，则小桥总长为。

查看试题解析
14. 如图是一块长方形ABCD的场地，长AB＝a米，宽AD＝b米，从A、B两处入口的小路宽都为1米，两小路汇合处路宽为2米，其余部分种植草坪，则草坪面积为平方米.

查看试题解析
15. 如图为甲、乙、丙三根笔直的钢管平行摆放在地面上的情形．已知乙有一部分只与甲重叠，其余部分只与丙重叠，甲没有与乙重叠的部分的长度为2m，丙没有与乙重叠的部分的长度为3m．若乙的长度最长且甲、乙的长度相差xm，乙、丙的长度相差ym，则乙的长度为m(用含有x、y的代数式表示)．

查看试题解析
16. 图1中的直角三角形有一条直角边长为3，将四个图1中的直角三角形分别拼成如图2，图3所示的正方形，其中阴影部分的面积分别记为 $S_{1} ， S_{2}$ ，则 $S_{1} - S_{2}$ 的值为．

查看试题解析

三、解答题

17. 青山绿水就是金山银山，为了加强环境保护，某地区进行河道环境改造，如图，某河段图形为长方形 $A B C D$ ，其长是 $n$ ，宽是 $m$ ，分别以 $A ， C$ 为圆心作扇形，用代数式表示阴影部分的周长 $L$ 和面积 $S$ .

查看试题解析
18. 一家住房的结构如下图所示，房子的主人打算把卧室以外的部分都铺上地板砖，至少需要多少平方米的地板砖？如果这种地板砖的价格为a元/平方米，那么购买地板砖至少需要多少元？

查看试题解析
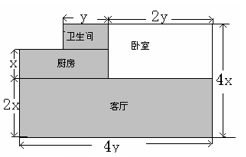19. 今年植树节时，某校有305名同学参加了植树活动，其中有 $\frac{2}{5}$ 的同学每人植树a棵，其余同学每人植树2棵，请求出他们植树的总棵数. $($ 用含a的代数式表示 $)$

查看试题解析
20. 如图，请你求出阴影部分的面积（用含有x的代数式表示）．

查看试题解析
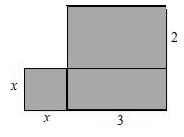21. 用不等式表示：

(1)、x的2倍与5的差不大于1；

(2)、x的 $\frac{1}{3}$ 与x的 $\frac{1}{2}$ 的和是非负数；

(3)、a与3的和不小于5；

(4)、a的20%与a的和大于a的3倍.

查看试题解析
22. 列式表示比a的6倍小3的数与比a的4倍大1的数，计算这两个数的和.

查看试题解析
23. 如图是某居民小区的一块长为 2a 米，宽为 b 米的长方形空地，为了美化环境，准备在这个长方形的四个顶点处修建一个半径为 $\frac{1}{2}$ b 米的扇形花台，然后在花台内种花，其余种草．如果建造花台及种花费用每平方米需要资金 100 元，种草每平方米需要资金 50 元，那么美化这块空地共需资金多少元？

查看试题解析

四、综合题

24. 甲、乙两个长方形的边长如图所示（ $m$ 为正整数），其面积分别为 $S_{1}$ ， $S_{2}$ ．

(1)、用含 $m$ 的代数式表示出 $S_{1}$ 和 $S_{2}$ ；

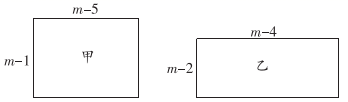(2)、比较 $S_{1}$ 和 $S_{2}$ 的大小， $S_{1}$ $S_{2}$ （用“＞”“＜”或“＝”进行连接）；

(3)、若一个正方形的周长等于甲、乙两个长方形的周长之和，求该正方形的面积（用含 $m$ 的代数式表示）．

查看试题解析