广西南宁市2021年秋季学期九年级数学期中义务教育质量监测
试卷更新日期:2021-08-15 类型:期中考试
一、选择题
-
1. 一元二次方程 ,经过配方可变形为( )A、 B、 C、 D、2. 已知反比例函数y (k≠0)的图象如图所示,则一次函数y=kx+2的图象经过( )
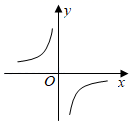 A、第一、二、三象限 B、第一、三、四象限 C、第一、二、四象限 D、第二、三、四象限3. 如图,已知 ∽ ,则下列哪条线段与 的比等于相似比( ).
A、第一、二、三象限 B、第一、三、四象限 C、第一、二、四象限 D、第二、三、四象限3. 如图,已知 ∽ ,则下列哪条线段与 的比等于相似比( ). A、 B、 C、 D、4. 如图, , 是 上直径 两侧的两点.设 ,则 ( )
A、 B、 C、 D、4. 如图, , 是 上直径 两侧的两点.设 ,则 ( ) A、 B、 C、 D、5. 如图,在 中,点 , , 分别在 , , 边上, , ,则下列式子一定正确的是( )
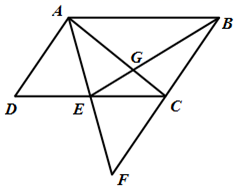
A、 B、 C、 D、5. 如图,在 中,点 , , 分别在 , , 边上, , ,则下列式子一定正确的是( ) A、 B、 C、 D、6. 如图,将 沿 边向右平移得到 , 交 于点G.若 . .则 的值为( )
A、 B、 C、 D、6. 如图,将 沿 边向右平移得到 , 交 于点G.若 . .则 的值为( ) A、2 B、4 C、6 D、87. 往水平放置的半径为 的圆柱形容器内装入一些水以后,截面图如图所示,若水面宽度 ,则水的最大深度为( )
A、2 B、4 C、6 D、87. 往水平放置的半径为 的圆柱形容器内装入一些水以后,截面图如图所示,若水面宽度 ,则水的最大深度为( )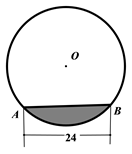 A、 B、 C、 D、8. 筒车是我国古代发明的一种水利灌溉工具,明朝科学家徐光启在《农政全书》中用图画描绘了筒车的工作原理,如图1,筒车盛水桶的运行轨道是以轴心O为圆心的圆,如图2,已知圆心O在水面上方,且 被水面截得的弦 长为6米, 半径长为4米.若点C为运行轨道的最低点,则点C到弦 所在直线的距离是( )
A、 B、 C、 D、8. 筒车是我国古代发明的一种水利灌溉工具,明朝科学家徐光启在《农政全书》中用图画描绘了筒车的工作原理,如图1,筒车盛水桶的运行轨道是以轴心O为圆心的圆,如图2,已知圆心O在水面上方,且 被水面截得的弦 长为6米, 半径长为4米.若点C为运行轨道的最低点,则点C到弦 所在直线的距离是( )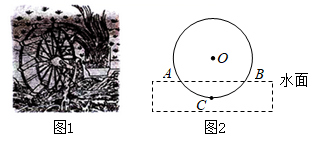 A、1米 B、 米 C、2米 D、 米9. 如图,在以 为直径的 中,点 为圆上的一点, ,弦 于点 ,弦 交 于点 ,交 于点 .若点 是 的中点,则 的度数为( )
A、1米 B、 米 C、2米 D、 米9. 如图,在以 为直径的 中,点 为圆上的一点, ,弦 于点 ,弦 交 于点 ,交 于点 .若点 是 的中点,则 的度数为( )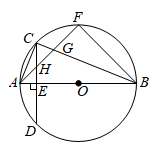 A、18° B、21° C、22.5° D、30°10. 抛物线 (a , b , c为常数, )与x轴交于 两点,与y轴的正半轴交于点C , 顶点为D . 有下列结论:
A、18° B、21° C、22.5° D、30°10. 抛物线 (a , b , c为常数, )与x轴交于 两点,与y轴的正半轴交于点C , 顶点为D . 有下列结论:① ;
② ;
③当 是等腰三角形时,a的值有2个;
④当 是直角三角形时, .
其中,正确结论的个数是( )
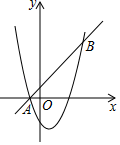
A、0 B、1 C、2 D、311. 在同一直角坐标系中,函数 与 的大致图象是( )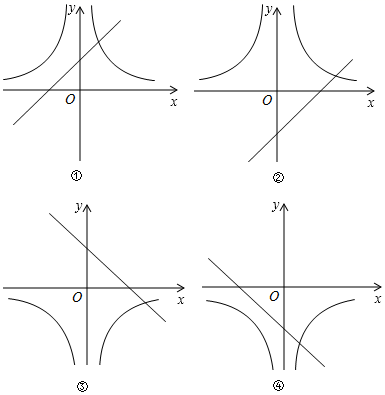 A、①② B、②③ C、②④ D、③④12. 如图,已知抛物线 与直线 交于 , 两点,则关于 的不等式 的解集是( )
A、①② B、②③ C、②④ D、③④12. 如图,已知抛物线 与直线 交于 , 两点,则关于 的不等式 的解集是( )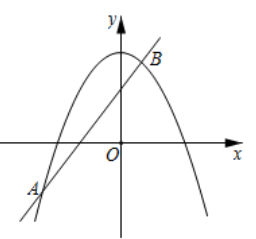 A、 或 B、 或 C、 D、
A、 或 B、 或 C、 D、二、填空题
-
13. 已知 ,它们的周长分别为 和 ,则 与 面积之比为.14. 如图,直线l1∥l2∥l3 , 分别交直线m、n于点A、B、C、D、E、F,若AB:BC=5:3,DE=15,则EF的长为.
 15. 如图, 是 的直径,点 在 上,若 ,则 °.
15. 如图, 是 的直径,点 在 上,若 ,则 °. 16. 如图,在⊙O内接四边形 中,若 ,则 .
16. 如图,在⊙O内接四边形 中,若 ,则 .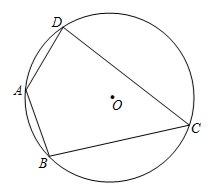 17. 如图所示的扇形中,已知 ,则 .
17. 如图所示的扇形中,已知 ,则 . 18. 我们规定:若 ,则 .例如 ,则 .已知 ,且 ,则 的最大值是.
18. 我们规定:若 ,则 .例如 ,则 .已知 ,且 ,则 的最大值是.三、解答题
-
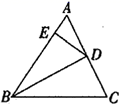
19. 解下列方程(1)、(2)、20. 如图,在△ABC中,BD平分∠ABC,交AC于点D,点E是AB上一点,连接DE,BD2=BC·BE.
证明:△BCD∽△BDE.
 21. 如图: ,CD⊥OA于D,CE⊥OB于E,求证:CD=CE.
21. 如图: ,CD⊥OA于D,CE⊥OB于E,求证:CD=CE.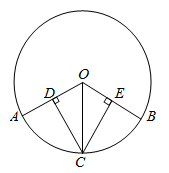 22. 已知:如图,AB是⊙O的直径,C、D是⊙O上两点, CM⊥AB,DN⊥AB,垂足分别为M、N, 弧AC=弧BD,求证:AM=BN.
22. 已知:如图,AB是⊙O的直径,C、D是⊙O上两点, CM⊥AB,DN⊥AB,垂足分别为M、N, 弧AC=弧BD,求证:AM=BN.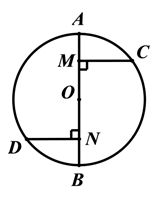 23. 如图,AB是 的直径,弦 于点E,若 , ,求 的长.
23. 如图,AB是 的直径,弦 于点E,若 , ,求 的长. 24. 如图, 是 的外接圆,点E是 的内心,AE的延长线交BC于点F,交 于点D,连接BD,BE.
24. 如图, 是 的外接圆,点E是 的内心,AE的延长线交BC于点F,交 于点D,连接BD,BE. (1)、求证: ;(2)、若 , ,求DB的长.
(1)、求证: ;(2)、若 , ,求DB的长.